Vous trouverez dans cette partie une synthèse de cet aspect des mathématiques. Si vous avez de bonnes connaissances en trigonométrie, vous pouvez passer à la rubrique suivante. En cas de difficulté de compréhension, consultez un ouvrage plus élémentaire.
Les fonctions trigonométriques servent principalement à modéliser ou à décrire :
- La relation entre les angles d'un triangle (d'où leur nom).
- Les rotations autour d'un cercle, y compris les positions en coordonnées polaires.
- Les valeurs cycliques ou périodiques, telles les ondes sonores.
Les fonctions trigonométriques de base sont dérivées de la rotation d'un angle autour d'un cercle unitaire.

Fonctions trigonométriques basées sur le cercle unitaire
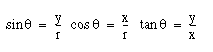
La fonction tangente n’est pas définie pour x = 0. Vous pouvez également définir la tangente comme suit :
Dans la mesure où XYR définit un triangle rectangle, la relation entre le sinus et le cosinus s'exprime comme suit:
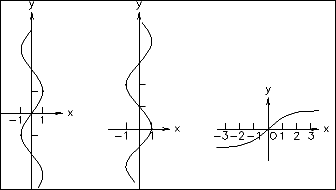
La représentation graphique des fonctions trigonométriques de base illustre leur nature cyclique :

Graphes des fonctions trigonométriques de base
Les fonctions sinus et cosinus produisent les mêmes valeurs, mais la phase diffère le long de l'axe des X de π/2 (en d'autres termes, 90 degrés).
Les fonctions inverses des fonctions trigonométriques sont les fonctions d’arc. La fonction inverse s’applique uniquement pour les valeurs de x limitées par -π/2 ≤ X ≤ π/2. Les graphes de ces fonctions s’affichent comme des graphes de fonctions trigonométriques de base, mais tournés sur le côté.
Graphes des fonctions d'arc de base
Les fonctions hyperboliques sont basées sur la constante exponentielle e et non sur une mesure circulaire. Elles se comportent cependant de manière similaire aux fonctions trigonométriques et sont nommées d'après elles. Fonctions hyperboliques de base :
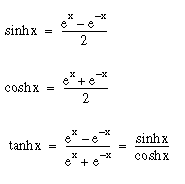
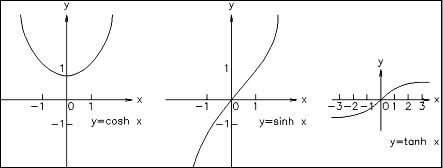
Graphes des fonctions hyperboliques de base