Hyperelastic Material Properties, Polynomial Form
Description: Defines material properties for use in fully nonlinear (i.e., large strain and large rotation) hyperelastic analysis of rubber-like materials (elastomers) for isoparametric solid elements.
Format:

Example:

| Field | Definition | Type | Default |
|---|---|---|---|
| MID | Material identification number. | Integer > 0 | Required |
| Aij | Material constants related to distortional deformation. | Real | 0.0 |
| Di | Material constants related to volumetric deformation. | Real ≥ 0 | 10 3 * (A10 + A01) for D1. 0.0 for D2 through D5 |
| RHO | Mass density in original configuration. | Real | 0.0 |
| AV | Volumetric coefficient of thermal expansion. | Real | 0.0 |
| TREF | Reference temperature for the calculation of thermal loads. | Real | 0.0 |
| GE | Structural element damping coefficient. See Remarks 7 and 9. | Real | 0.0 |
| NA | Order of the distortional strain energy polynomial function. | 0 < Integer ≤ 5 | 1 |
| ND | Order of the volumetric strain energy polynomial function. | 0 < Integer ≤ 5 | 1 |
| TAB1 | Table identification number of
TABLES1 entry that contains simple tension/compression data to be used in the estimation of the material constants Aij. xi values in the TABLES1 entry must be stretch ratios
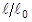 and yi values must be values of the engineering stress and yi values must be values of the engineering stress
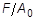 . Stresses are negative for compression and positive for tension. If this convention is not followed the solution may fail to converge. . Stresses are negative for compression and positive for tension. If this convention is not followed the solution may fail to converge.
|
Integer > 0 or blank | |
| TAB2 | Table identification number of TABLES1 entry that contains equibiaxial tension data to be used in the estimation of the material constants Aij. xi values in the TABLES1 entry must be stretch ratios
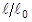 . yi values must be values of the engineering stress . yi values must be values of the engineering stress
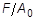 . .
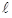 is the current length, is the current length,
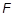 is the current force, is the current force,
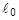 is the initial length and is the initial length and
 is the cross-sectional area. In the case of pressure of a spherical membrane, the engineering stress is given by is the cross-sectional area. In the case of pressure of a spherical membrane, the engineering stress is given by
 , where , where
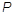 is the current value of the pressure and is the current value of the pressure and
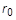 , ,
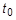 is the initial radius and thickness. is the initial radius and thickness.
|
Integer > 0 or blank | |
| TAB3 | Table identification number of TABLES1 entry that contains simple shear data to be used in the estimation of the material constants Aij. xi values in the TABLES1 entry must be values of the shear tangent
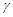 and yi values must be values of the engineering stress and yi values must be values of the engineering stress
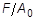 . .
|
Integer > 0 or blank | |
| TAB4 | Table identification number of TABLES1 entry that contains pure shear data to be used in the estimation of the material constants Aij. xi and yi values in the TABLES1 entry must be stretch ratios
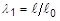 and values of the nominal stress and values of the nominal stress
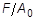 . .
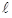 is the current length, is the current length,
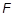 is the current force, is the current force,
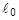 and and
 are the initial length and cross-sectional area, respectively in the 1-direction. are the initial length and cross-sectional area, respectively in the 1-direction.
|
Integer > 0 or blank | |
| TABD | Table identification number of TABLES1 entry that contains pure volumetric compression data to be used in the estimation of the material constants Di. xi values in the TABLES1 entry must be values of the volume ratio
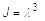 , where , where
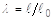 is the stretch ratio in all three directions; yi values must be values of the pressure, assumed positive in compression. is the stretch ratio in all three directions; yi values must be values of the pressure, assumed positive in compression.
|
Integer > 0 or blank |
Remarks:
- The generalized Mooney-Rivlin strain energy may be expressed as follows:
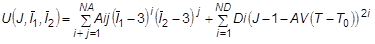
where
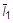 and
and
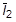 are the first and second distortional strain invariants, respectively;
are the first and second distortional strain invariants, respectively;
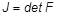 is the determinate of the deformation gradient; and 2D1 =
K and 2(A10 + A01) =
G at small strains, in which
K is the bulk modulus. The model reduces to a Mooney-Rivlin material if NA = 1 and to a Neo-Hookean material if NA = 1 and A01 = 0.0 (See Remark 2). For Neo-Hookean or Mooney-Rivlin materials no continuation entry is required.
is the determinate of the deformation gradient; and 2D1 =
K and 2(A10 + A01) =
G at small strains, in which
K is the bulk modulus. The model reduces to a Mooney-Rivlin material if NA = 1 and to a Neo-Hookean material if NA = 1 and A01 = 0.0 (See Remark 2). For Neo-Hookean or Mooney-Rivlin materials no continuation entry is required.
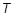 is the current temperature and
is the current temperature and
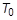 is the initial temperature.
is the initial temperature.
- Hyperelastic materials show a fully incompressible or nearly incompressible behavior. Full incompressibility is not presently available, while nearly incompressible behavior can be simulated using a large value of D1.
- Aij and Di are obtained from least squares fitting of experimental data. One or more of four experiments (TAB1 to TAB4) may be used to obtain Aij. Di may be obtained from pure volumetric compression data (TABD). If all TAB1 through TAB4 are blank, Aij must be specified by the user. Parameter estimation, specified through any of the TABLES1 entries, supersedes the manual input of the parameters.
- If ND = 1 and a nonzero value of D1 is provided or is obtained from experimental data in TABD, then the parameter estimation of the material constants Aij takes compressibility into account in the cases of simple tension/compression, equibiaxial tension, and general biaxial deformation. Otherwise, full incompressibility is assumed in estimation the material constants.
- The mass density, RHO, will be used to automatically compute mass for all structural elements.
- Weight density may be used in field 9 if the value 1/g is entered on the PARAM, WTMASS entry, where g is the acceleration of gravity.
- To obtain the damping coefficient GE, multiply the critical damping ratio C/C0, by 2.0.
- TREF is used only as the reference temperature for the calculation of thermal loads in linear solutions. If TEMPERATURE(INITIAL) is specified, TREF will be ignored.
- If PARAM, W4 is not specified, GE is ignored in transient response analysis. (See Section 5, Parameters, for more information on W4.)