PCOMP

Layered Composite Element Property

Description: Defines the properties of an n-ply composite material laminate.

Format:

Example:

Field Definition Type Default
PID Property identification number. Integer > 0 Required
Z0 Distance from the reference plane to the bottom surface. Real -1/2 element thickness
NSM Nonstructural mass per unit area. Real 0.0
SB Allowable inter-laminar shear stress of the bonding material (allowable interlaminar shear stress). Required if bond shear failure index/strength ratio is desired. Real > 0.0
FT Ply failure theory. The following theories are allowed. (If blank, then no failure calculation is performed.)
HILL for the Hill theory
HOFF for the Hoffman theory
TSAI for the Tsai-Wu theory
STRESS for the maximum stress theory
STRAIN/STRN for the maximum strain theory
LARC02 for the NASA LaRC theory
PUCK for the Puck PCP theory
MCT for the Multicontinuum Theory
Character or blank See Remark 16
TREF Reference temperature. See Remark 3. Real 0.0
GE Structural element damping coefficient. See Remarks 12 and 13. Real 0.0
LAM Laminate option, one of the following character variables: SYM, HCS, FCS, ACS, SME, or SMC. If LAM = SYM, only plies on one side of the element centerline are specified. The plies are numbered starting with 1 for the bottom layer. If an odd number of plies is desired with LAM = SYM, then the center ply thickness (Ti) should be half the actual thickness. If LAM = HCS, LAM = FCS, or LAM = ACS, a composite sandwich is defined for the purpose of facesheet stability index output. HCS specifies a honeycomb core material, FCS specifies a form core material, and ACS selects either HCS or FCS based on the core material specified. If LAM = SME, the ply effects are smeared and the stacking sequence is ignored. If LAM = SMC, a composite sandwich is defined using equivalent orthotropic properties. See Remarks 7 through 9. Character or blank If blank, all plies must be specified
MIDi Material identification number of the various plies. The plies are identified by serially numbering them from 1 at the bottom layer. The MIDs must refer to MAT1, MAT2, MAT4, MAT5, MAT8, or MAT12 Bulk Data entries. See Remark 11. Integer > 0 MID1 required, see Remark 1
Ti Ply thickness. See Remark 1. Real or blank T1 required
THETAi Orientation angle of the longitudinal direction of each ply with the material axis of the element. (If the material angle on the element connection entry is 0.0, the material axis and side 1-2 of the element coincide.) The plies are numbered serially starting with 1 at the bottom layer. The bottom layer is defined as the surface with the largest -Z value in the element coordinate system. Real or blank 0.0
SOUTi Stress or strain output request, one of the following character variables: YES or NO. Character NO

Remarks:

  1. The default for MID2, …, MIDn is the last defined MIDi. In the example above MID1 is the default for MID2, MID3, and MID4. The same logic applies to Ti.
  2. At least one of the four values (MIDi, Ti, THETAi, SOUTi) must be present for a ply to exist. The minimum number of plies is one.
  3. When PARAM, TEMPDEPCOMP is set to OFF (default is ON), the TREF given on the PCOMP entry will be used for all plies of the element and will override values supplied on material entries for individual plies. If the PCOMP entry references temperature-dependent material properties, then TREF given on the PCOMP will be used as the temperature to determine material properties and TEMPERATURE Case Control commands will be ignored for deriving the equivalent PSHELL and MAT1 entries used to describe the composite element. (See Section 5, Parameters, for more information on TEMPDEPCOMP.)
  4. If PARAM, NOCOMPS is set to 1, or OFF, then composite element ply results will be output while the equivalent homogeneous element results will be suppressed. If PARAM, NOCOMPS is set to -1, 0 or ON, then composite element ply results will be suppressed while the equivalent homogeneous element results will be output.
  5. When PARAM, COMPILSMETHOD is set to COMPONENT (default), the failure index for the bonding material is calculated as Failure Index = max(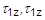). (See Section 5, Parameters, for more information on COMPILSMETHOD.) The Failure Index for the ply is calculated as shown in the table below.
    Theory Failure Index Remarks
    Hill 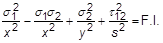Orthotropic materials with equal strengths in tension and compression.
    Hoffman 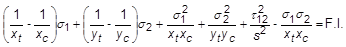Orthotropic materials under a general state of plane stress with unequal tensile and compressive strengths.
    Tsai-Wu 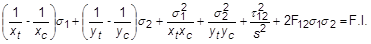Orthotropic materials under a general state of plane stress with unequal tensile and compressive strengths.
    LaRC02 See the Autodesk Nastran User's Manual, Reference 5. Orthotropic materials comprised of unidirectional plies under a general state of plane stress.
    Puck See the Autodesk Nastran User's Manual, References 12 and 13. Orthotropic materials comprised of unidirectional plies under a general state of plane stress.
    MCT See the Autodesk Nastran User's Manual, References 20, 21, and 22. Orthotropic materials comprised of unidirectional plies or plain weave fabric under a general state of plane stress.
    Max Stress Max 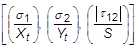None
    Max Strain Max None

    For LaRC02 and Puck failure theories, the plies must reference an orthotropic, unidirectional material. Materials with stiffness or allowable ratios (axial/lateral) less than the value defined by the LARC02TSAITOL model parameter will automatically revert to the Tsai-Wu failure theory. (See Section 5, Parameters, for more information on LARC02TSAITOL.)

  6. The STRENGTHRATIO model parameter is used to request the output of the Tsai Strength Ratio (R) instead of Failure Index. (See Section 5, Parameters, for more information on STRENGTHRATIO.)
  7. The LAM field (FCS, HCS, or ACS options) can be used to define a composite sandwich laminate which consists of lower facesheet plies, followed by a single core ply (foam or honeycomb), and then upper facesheet plies. The number of plies defined must be greater than or equal to 3. When the total number of plies is greater than 3, the ply with the minimum equivalent material extensional stiffness is selected as the core ply automatically. Output includes facesheet stability indexes for three failure modes: wrinkling, dimpling, and crimping. Stability indexes are calculated using:

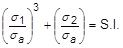
    Where 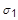and are the maximum and minimum facesheet principal stresses and 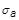is the facesheet allowable. If 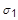is positive, the stability index is calculated using:

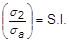
    If is positive, the stability index will be zero.

  8. The SME and SMC options are used to define properties where the ply stacking sequence and membrane-bending coupling effects are ignored. The SME option smears the laminate material stiffness properties. The SMC option allows simplified modeling of a sandwich panel with equal face sheets and a central core. Output is for the equivalent homogeneous element and does not include individual ply results.
  9. FCS, HCS, ACS, and SMC are all used to define sandwich laminate properties. FCS, HCS, and ACS define a composite laminate sandwich where the plies are specified in sequence from the bottom face sheet outer ply through to the top face sheet outer ply. Laminate properties and results are calculated the same as with the SYM or default laminate options with the addition of face sheet stability index output. SMC defines a simplified sandwich panel with equal face sheets and a central core. The facesheet plies are specified first followed by the core ply last. Stability index output is not available with the SMC option.
  10. A function of this entry is to derive equivalent internal PSHELL and MATi entries to describe the composite element. These equivalent entries are given in the database definition section of the Model Results Output File and in the translated Bulk Data Output File.
  11. This entry may be used to define either a layered shell or solid element. For shell elements the MIDi fields may only reference MAT1, MAT2, or MAT8 entries. For solid elements the MIDi fields may only reference MAT1, MAT9, or MAT12 entries.
  12. To obtain the damping coefficient GE, multiply the critical damping ratio C/C 0, by 2.0.
  13. If PARAM, W4 is not specified, GE is ignored in transient response analysis. (See Section 5, Parameters, for more information on W4.)
  14. To compute a ply and/or bond failure index/strength ratio, the STRESS or STRAIN Case Control command must be present, SOUTi must be set to YES, and the following must be defined:
    • For a ply stress or strain failure index/strength ratio:
      • FT on the PCOMP or the referenced MIDi entry
      • The stress or strain allowables on the referenced MIDi entry
    • For a bond failure index/strength ratio:
      • The stress allowable SB on the PCOMP or referenced MIDi entry
  15. Ply stress and strain results are always computed in the ply coordinate system.
  16. If FT = STRN:
    • For PCOMP with MAT1 - In MAT1 card, field FT should be STRAIN
    • For PCOMP with MAT8 - In MAT8 card, field STRN should be 1.0
Parent topic: Section 4: Bulk Data