Per ulteriori informazioni, vedere Come definire le pile di tolleranza.
Derivare le equazioni di base per le catene di quote lineari chiuse dall'immagine seguente.

a = 32 ± 1,5 mm, b = 8 ± 1 mm
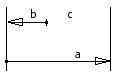
Elementi crescenti/decrescenti
Se aumenta l'elemento crescente, aumenterà anche l'elemento di chiusura. Se aumenta l'elemento decrescente, l'elemento di chiusura diminuirà a patto che gli altri elementi della catena non vengano alterati.
|
Elemento di chiusura: |
1. c = a - b |
|
Quota limite superiore dell'elemento di chiusura: |
2. c max = a max - b min |
|
Quota limite inferiore dell'elemento di chiusura: |
3. c min = a min - b max |
|
Tolleranza dell'elemento di chiusura (sottrazione dell'equazione 3 dall'equazione 2) |
4. c max - c min = a max - a min - (b min - b max ) |
|
Quale |
5. T c = T a + T b |
In generale, le tolleranze delle catene lineari soddisfano l'equazione seguente.
![]()
Analogamente, è possibile scrivere le equazioni 2 e 3 in un modulo generale.
![]()
![]()
La quota limite superiore dell'elemento di chiusura corrisponde ad una differenza della somma delle quote limite superiori degli elementi crescenti e della somma delle quote limite inferiori degli elementi decrescenti.
La quota limite inferiore dell'elemento di chiusura corrisponde ad una differenza della somma delle quote limite inferiori degli elementi crescenti e della somma delle quote limite superiori degli elementi decrescenti.
La quota nominale dell'elemento di chiusura può essere espressa mediante l'equazione 1, come nell'equazione seguente.
![]()
Limite deviazione superiore dell'elemento di chiusura.
![]()
Limite deviazione inferiore dell'elemento di chiusura.
![]()