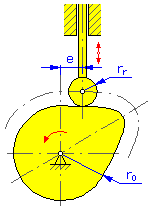
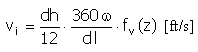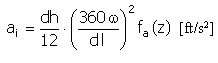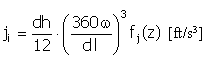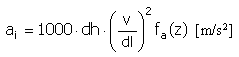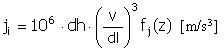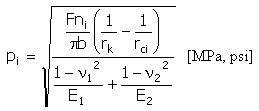Dati di input:
- Raggio di base r 0 (camme cilindriche e a disco)
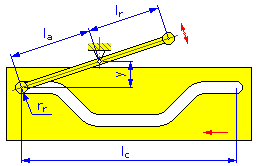
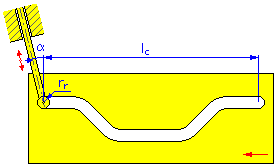
- Lunghezza movimento l c (camme lineari)
- Larghezza camma b c
- Raggio rullo r r
- Larghezza rullo b r (cilindro forma cedente)
- Eccentricità e (camme a disco per cedente di conversione)
- Angolo di eccentricità α (camme lineari e cilindriche per cedente traslatorio)
- Distanza perno y (camme a disco e lineari per braccio oscillante)
- Lunghezza braccio l a (camme a disco e lineari per braccio oscillante)
- Braccio di reazione l a (camme a disco e lineari per braccio oscillante)
- Velocità ω (camme a disco e cilindriche)
- Velocità v (camme lineari)
- Forza su rullo F
- Peso accelerato m
- Livello elasticità c
- Pressione ammissibile p A1
- Modulo di elasticità del materiale camma E 1
- Coefficiente di Poisson del materiale camma μ 1
- Pressione ammissibile p A2
- Modulo di elasticità del materiale cedente E 2
- Coefficiente di Poisson del materiale eccedente μ 2
|
Camme a disco |
|
|
|
|
|
Camme lineari |
|
|
|
|
|
Camme cilindriche |
|
 |
|
|
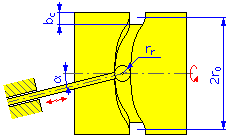
Diametro esterno = 2r 0 + b c |
|
|
Diametro interno = 2r 0 - b c |
|
Segmenti camma
- Funzione movimento f y (z) [ul]
- Rapporto di inversione k r (solo per moto parabolico e parabolico con parte lineare)
- Parte lineare k l (solo per moto parabolico con parte lineare)
- Posizione iniziale movimento l 0 [°; mm, in]
- Posizione finale movimento l [°; mm, in]
- Lunghezza movimento segmento dl = l - l 0 [°; mm, in]
- Alzata iniziale h 0 [mm, in]
- Alzata all'estremità h max [mm, in]
- Segmento alzata d h = h max - h 0 [mm, in]
Dipendenze da alzata
Camma cilindrica e a disco
Angolo di rotazione camma ϕ i [°]
Posizione relativa effettiva nel segmento: z i = (ϕ i - L 0 ) / dl (intervallo 0 - 1)
|
Alzata |
y i = dh f y (z) [mm, in] |
|
Velocità |
|
|
|
|
|
Accelerazione |
|
|
|
|
|
Impulso |
|
|
|
Camme lineari
Posizione movimento camma l i [mm, in]
Posizione relativa effettiva nel segmento: z i = (l i - l 0 ) / dl (intervallo 0 - 1)
|
Alzata |
y i = dh f y (z) [mm, in] |
|
Velocità |
|
|
Accelerazione |
|
|
|
|
|
Impulso |
|
|
|
Funzioni movimento
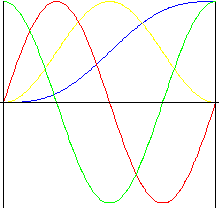
Cicloidale (sinusoidale esteso)
Questo movimento presenta caratteristiche di accelerazione eccellenti. Viene spesso usato per camme ad alta velocità in quanto risulta efficace in presenza di livelli bassi di rumore, vibrazioni e usura.
|
|
Alzata |
|
|
Velocità |
|
|
Accelerazione |
|
|
Impulso |
|
Alzata |
f y (z) = z - 0,5/π sin(2πz) |
|
Velocità |
f v (z) = 1 - cos (2πz) |
|
Accelerazione |
f a (z) = 2π sin(2πz) |
|
Impulso |
f j (z) = 4π 2 cos(2πz) |
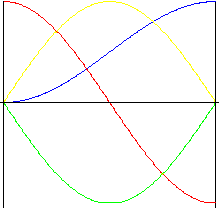
Armonico (sinusoidale)
Il vantaggio caratteristico di questa curva è la scorrevolezza della velocità e dell'accelerazione durante la corsa. Tuttavia, gli sbalzi repentini di accelerazione nella parte iniziale e finale del movimento tendono a causare vibrazioni, rumore e usura.
|
|
Alzata |
|
|
Velocità |
|
|
Accelerazione |
|
|
Impulso |
|
Alzata |
f y (z) = 0,5 (1 - cos πz)) |
|
Velocità |
f v (z) = 0,5 π sin (πz) |
|
Accelerazione |
f a (z) = 0,5 π 2 cos(πz) |
|
Impulso |
f j (z) = -0,5π 3 sin(πz) |
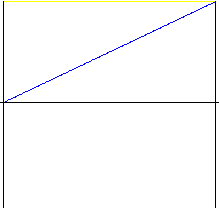
Lineari
Movimento semplice con un forte shock nella parte iniziale e fina del movimento. Usato raramente, tranne nei dispositivi particolarmente rudimentali. Si consiglia di usare un movimento con le parti iniziale e finale modificate - Parabolico con parte lineare.
|
|
Alzata |
|
|
Velocità |
|
Alzata |
f y (z) = z |
|
Velocità |
f v (z) = 1 |
|
Accelerazione |
f a (z) = 0 |
|
Nota: per z = 0 e z = 1 il valore corretto dovrebbe essere un valore infinito, ma il calcolo non può funzionare con un valore infinito e pertanto viene utilizzato un valore zero.
|
|
|
Impulso |
f j (z) = 0 |
|
Nota: per z = 0 e z = 1 il valore corretto dovrebbe essere un valore infinito, ma il calcolo non può funzionare con un valore infinito e pertanto viene utilizzato un valore zero.
|
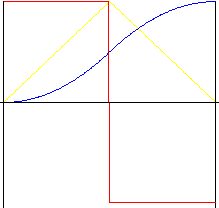
Parabolico (polinomiale di 2 ° grado)
Movimento con la minima accelerazione possibile. Tuttavia, gli sbalzi repentini di accelerazione nella parte iniziale, centrale e finale del movimento provocano shock. Il rapporto di inversione consente di "stirare" la parte centrale del movimento, per consentire modifiche al rapporto di accelerazione e decelerazione.
simmetrico (rapporto di inversione k r = 0.5)
|
|
Alzata |
|
|
Velocità |
|
|
Accelerazione |
|
per z = da 0 a 0,5: |
|||
|
Alzata |
fy(z) = 2z 2 |
||
|
Velocità |
fv(z) = 4z |
||
|
Accelerazione |
fa (z) = 4 |
||
|
Impulso |
fa(z) = 0 |
||
|
per z = 0,5 - 1: |
|||
|
Alzata |
fy(z) = 1 - 2(1 - z) 2 |
||
|
Velocità |
fv(z) = 4 (1 - z) |
||
|
Accelerazione |
fa (z) = -4 |
||
|
Impulso |
fj(z) = 0 |
||
|
Nota: per z = 0 e z = 1 il valore corretto dovrebbe essere un valore infinito, ma il calcolo non può funzionare con un valore infinito e pertanto viene utilizzato un valore zero.
|
|||
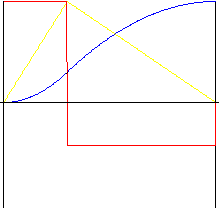
non simmetrico
k r - rapporto di inversione (nell'intervallo compreso tra 0,01 e 0,99)
|
|
Alzata |
|
|
Velocità |
|
|
Accelerazione |
|
per z = 0 a k r : |
|||
|
Alzata |
f y (z) = z 2 / k r |
||
|
Velocità |
f v (z) = 2z / k r |
||
|
Accelerazione |
f a (z) = 2 / k r |
||
|
Impulso |
f j (z) = 0 |
||
|
per z = k r a 1: |
|||
|
Alzata |
f y (z) = 1 – (1 – z) 2 / (1 – k r ) |
||
|
Velocità |
f v (z) = 2 (1 – z) / (1 – k r ) |
||
|
Accelerazione |
f a (z) = -2 / (1 - k r ) |
||
|
Impulso |
f j (z) = 0 |
||
|
Nota: per z = 0 e z = 1 il valore corretto dovrebbe essere un valore infinito, ma il calcolo non può funzionare con un valore infinito e pertanto viene utilizzato un valore zero.
|
|||
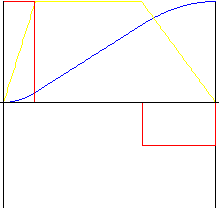
Parabolico con parte lineare
Assicura un'accelerazione e una decelerazione più accettabili rispetto al movimento lineare. Il rapporto di inversione consente di "stirare" la parte centrale del movimento, per consentire modifiche al rapporto di accelerazione e decelerazione. Il rapporto parte lineare consente di impostare una dimensione relativa della parte del movimento lineare.
|
|
Velocità |
|
|
Accelerazione |
|
|
Impulso |
k r - rapporto di inversione (nell'intervallo compreso tra 0,01 e 0,99)
k l - rapporto parte lineare (nell'intervallo compreso tra 0 e 0,99)
k z = 1 + k l / (1 - k l )
k h = (1 - k l ) / (1 + k l )
|
per z = 0 a k r / k z : |
|||
|
Alzata |
f y (z) = k h z 2 k z 2 / k r |
||
|
Velocità |
f v (z) = 2 k h z k z 2 / k r |
||
|
Accelerazione |
f a (z) = 2 k h k z 2 / k r |
||
|
Impulso |
f j (z) = 0 |
||
|
per z = k r / k z a r / k z + k l : |
|||
|
Alzata |
f y (z) = (z - 0,5 k r / k z ) 2 / (1 + k l ) |
||
|
Velocità |
f v (z) = 2 / (1 + k l ) |
||
|
Accelerazione |
f a (z) = 0 |
||
|
Impulso |
f j (z) = 0 |
||
|
per z = k r / k z + k l a 1: |
|||
|
Alzata |
f y (z) = 1 - k h (1 - z) 2 k z 2 / (1 - k r ) |
||
|
Velocità |
f v (z) = 2 k h (1 - z) k z 2 / (1 - k r ) |
||
|
Accelerazione |
f a (z) = -2 k h k z 2 / (1 - k r ) |
||
|
Impulso |
f j (z) = 0 |
||
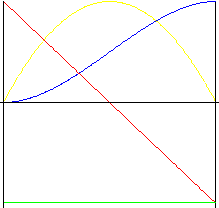
Polinomiale di 3 ° grado (parabola cubica)
Movimento caratterizzato da shock minori rispetto al movimento parabolico.
|
|
Alzata |
|
|
Velocità |
|
|
Accelerazione |
|
|
Impulso |
|
Alzata |
f y (z) = (3 -2z) z 2 |
|
Velocità |
f v (z) = (6 - 6z) z |
|
Accelerazione |
f a (z) = 6 - 12z |
|
Impulso |
f j (z) = -12 |
Polinomiale di 4 ° grado
Movimento caratterizzato da shock minori rispetto al movimento polinomiale di 3 ° grado.

|
|
Alzata |
|
|
Velocità |
|
|
Accelerazione |
|
|
Impulso |
|
per z = 0 - 0,5 |
||
|
Alzata |
f y (z) = (1 - z) 8z 3 |
|
|
Velocità |
f v (z) = (24 - 32z) z 2 |
|
|
Accelerazione |
f a (z) = (48 - 96z) z |
|
|
Impulso |
f j (z) = 48 - 192z |
|
|
per z = 0,5 - 1 |
||
|
Alzata |
f y (z) = 1 - 8z (1 - z) 3 |
|
|
Velocità |
f v (z) = (32z - 8) (1 - z) 2 |
|
|
Accelerazione |
f a (z) = (48 - 96z) (1 - z) |
|
|
Impulso |
f j (z) = 194z - 144 |
|
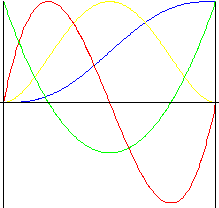
Polinomiale di 5 ° grado
Movimento caratterizzato da shock minori rispetto al movimento polinomiale di 3 ° grado.
|
|
Alzata |
|
|
Velocità |
|
|
Accelerazione |
|
|
Impulso |
|
Alzata |
f y (z) = (6z 2 - 15z + 10) z 3 |
|
Velocità |
f v (z) = (z 2 - 2z + 1) 30z 2 |
|
Accelerazione |
f a (z) = (2z 2 - 3z + 1) 60z |
|
Impulso |
f j (z) = (6z 2 - 6z + 1) 60 |
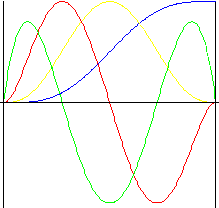
Polinomiale di 7 ° grado
Scorrevolezza in tutte le formule incluso l'impulso.
|
|
Alzata |
|
|
Velocità |
|
|
Accelerazione |
|
|
Impulso |
|
Alzata |
f y (z) = (-20z 3 + 70z 2 - 84z + 35) z 4 |
|
Velocità |
f v (z) = (-z 3 + 3z 2 - 3z + 1) 140z 3 |
|
Accelerazione |
f a (z) = (-2z 3 + 5z 2 - 4z + 1) 420z 2 |
|
Impulso |
f j (z) = (-5z 3 + 10z 2 - 6z + 1) 840z |
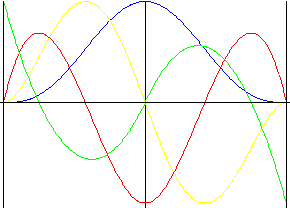
Polinomiale non simmetrico di 5 ° grado
Simile al polinomiale di 5° grado, ma con ritorno di alzata forzato.
|
|
Alzata |
|
|
Velocità |
|
|
Accelerazione |
|
|
Impulso |
|
Parte 1 |
||
|
Alzata |
f y (z) = 1 - (8 (1 - z) 3 - 15 (1 - z) 2 + 10) (1 - z) 2 / 3 |
|
|
Velocità |
f v (z) = (2 (1 - z) 3 - 3 (1 - z) 2 + 1) (1 - z) 20 / 3 |
|
|
Accelerazione |
f a (z) = -(8 (1 - z) 3 - 9 (1 - z) 2 + 1) 20 / 3 |
|
|
Impulso |
f j (z) = (4 (1 - z) 2 - 3 (1 - z)) 40 |
|
|
Parte 2 |
||
|
Alzata |
f y (z) = (8z 3 - 15z 2 + 10) z 2 / 3 |
|
|
Velocità |
f v (z) = (2z 3 - 3z 2 + 1) z 20/3 |
|
|
Accelerazione |
f a (z) = (8z 3 - 9z 2 + 1) 20/3 |
|
|
Impulso |
f j (z) = (4z 2 - 3z) 40 |
|
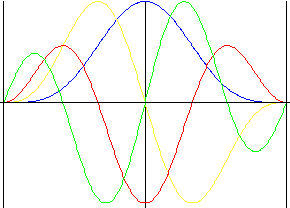
Armonico doppio
Scorrevolezza in tutte le formule incluso l'impulso con ritorno di alzata forzato.
|
Parte 1 |
||
|
Alzata |
f y (z) = cos(0,5π (1 - z)) 4 |
|
|
Velocità |
f v (z) = π (0,5 sin(πz) - 0,25 sin(2πz)) |
|
|
Accelerazione |
f a (z) = 0,5 π 2 (cos(πz) - cos(2πz)) |
|
|
Impulso |
f j (z) = π 3 (-0,5 sin(πz) + sin(2πz)) |
|
|
Parte 2 |
||
|
Alzata |
f y (z) = 1 - cos(0,5π z) 4 |
|
|
Velocità |
f v (z) = π (0,5 sin(πz) + 0,25 sin(2πz)) |
|
|
Accelerazione |
f a (z) = 0,5 π 2 (cos(πz) + cos(2πz)) |
|
|
Impulso |
f j (z) = -π 3 (0,5 sin(πz) + sin(2πz)) |
|
Confronto tra valori relativi massimi
|
Movimento |
Velocità |
Accelerazione |
Impulso |
|
Cicloidale (sinusoidale esteso) |
2 |
6,28 |
39,5 |
|
Armonico (sinusoidale) |
1,57 |
4,93 |
15,5 |
|
Lineare |
1 |
∞ |
∞ |
|
Parabolico (polinomiale di 2 ° grado) |
2 |
4 |
∞ |
|
Polinomiale di 3 ° grado |
1,5 |
6 |
12 |
|
Polinomiale di 4 ° grado |
2 |
6 |
48 |
|
Polinomiale di 5 ° grado |
1,88 |
5,77 |
60 |
|
Polinomiale di 7 ° grado |
2,19 |
7,51 |
52,5 |
|
Polinomiale non simmetrico di 5 ° grado |
1,73 |
6,67 |
40 |
|
Armonico doppio |
2,04 |
9,87 |
42,4 |
Altre dipendenze
Forza sul rullo
|
F i = F + m a i + c y i [N, lb] |
Forza normale
|
Fn i = F i / cos (γ i ) [N, lb] |
Momento
|
T i = F i r i tan (γ i ) [Nmm, lb in] |
Pressione specifica (Hertz)
|
|
|
|
b = min (b v, b k ) |