자세한 내용은 공차 누적을 정의하려면을 참조하십시오.
다음 이미지에서 닫힌 선형 치수 체인에 대한 기본 공식을 추출합니다.
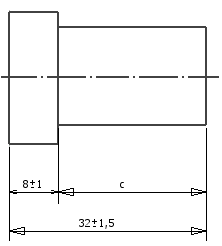
a = 32 ± 1.5 mm, b = 8 ± 1 mm
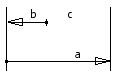
증가/감소 요소
증가 요소가 증가하면 닫힘 요소도 증가합니다. 체인의 다른 요소가 일정한 경우 감소 요소가 증가하면 닫힘 요소가 감소합니다.
|
닫힘 요소: |
1. c = a - b |
|
닫힘 요소의 상한 한계 치수: |
2. c max = a max - b min |
|
닫힘 요소의 하한 한계 치수: |
3. c min = a min - b max |
|
닫힘 요소의 공차(방정식 2에서 방정식 3을 뺌) |
4. c max - c min = a max - a min - (b min - b max ) |
|
예: |
5. T c = T a + T b |
일반적으로 선형 체인 공차는 다음 공식을 만족시킵니다.
![]()
마찬가지로 공식 2와 3을 일반 형태로 쓸 수 있습니다.
![]()
![]()
닫힘 요소의 상한 한계 치수는 증가 요소의 상한 한계 치수의 합과 감소 요소의 하한 한계 치수의 합의 차이와 같습니다.
닫힘 요소의 하한 한계 치수는 증가 요소의 하한 한계 치수의 합과 감소 요소의 상한 한계 치수의 합의 차이와 같습니다.
닫힘 요소의 공칭 치수는 다음 공식에서처럼 공식 1을 사용하여 표현할 수 있습니다.
![]()
닫힘 요소의 상한 한계 편차:
![]()
닫힘 요소의 하한 한계 편차:
![]()