V-벨트 강도 비율 계산

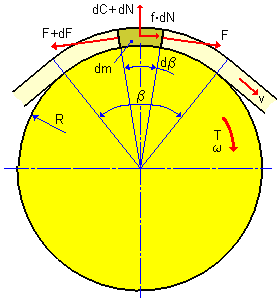
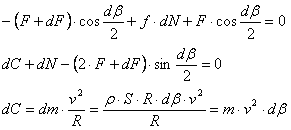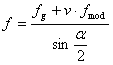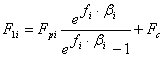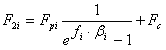일반적으로 사용되는 방정식

	여기에서 m은 벨트의 고유 질량으로 m = S ρ로 정의됩니다.

주어진 풀리의 수정 마찰계수

	f = f g + v f mod

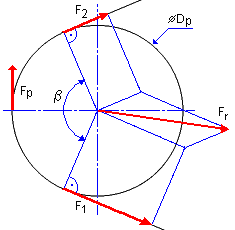
연동 풀리 및 벨트 기본 방정식

전달할 동력

벨트 속도

벨트 플렉스 진동수

유효 인장(또는 유효 장력)

원심력

Fc = z m v ²

벨트 스팬의 장력

다음 방정식에서 응용프로그램은 하중을 전달하는 데 최대 벨트 장착 장력이 필요할 것으로 가장 의심되는 풀리를 먼저 결정합니다. 그런 다음 초기 벨트 장착 장력에 따라 모든 풀리에 대해 각 스팬의 벨트 장력을 조정합니다.

	F 1i - F p P xi - F 2i = 0

가장 의심되는 풀리 기준은 견고한 면의 최대 장력입니다.

F _1max = max (F _1i )

벨트가 전체 하중에서 구동될 때 벨트 스팬의(벨트당) 전체 최대 장력은 다음과 같이 결정됩니다.

여기서 표현식 "k ₁ F _1max "는 벨트 드라이브의 모든 벨트에 대해 고려되는 벨트 스팬의 실제 최대 인장입니다. 이러한 방식으로 개별 스팬의 모든 해당 인장은 다음 조건을 충족하도록 다시 계산됩니다.

F _1i - F _P P _xi - F _2i = 0

벨트가 전체 하중에서 구동될 때 각 풀리의 결과 축 하중

주: 연계 풀리와 아이들러의 경우 F ₁ 및 F ₂ 가 생성기 내에서 반전되어 있으므로 벨트 동작 측면에서 F ₁ 은 입력 시 벨트 스팬 인장이 되고 F ₂ 는 출력 시 벨트 스팬 인장이 됩니다.

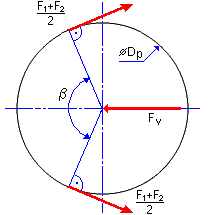
벨트 초기 장착 장력 및 정적 인장 조정 힘

필요한 벨트 초기 장착 장력(벨트당)은 인장 조정 힘에 따라 조정된 후 다음과 같이 결정됩니다.

각 풀리에 대해 정적 인장 조정 힘 F _v 가 결정됩니다. 응용프로그램은 다음과 같이 벨트 스팬의 중심선을 따라 수행되는 인장 조정 힘을 계산합니다.

사용된 변수의 의미:

F	접선력 [N]
β	접촉 호 [도]
α	쐐기 각도 [도]
C	원심력 [N]
N	법선력 [N]
m	고유 벨트 질량 [kg/m]
v	벨트 속도 [m/s]
R	풀리 반지름 [m]
S	벨트 횡단면 영역[m 2 ]
T	주어진 풀리에 작용하는 토크 [Nm]
D p	풀리 피치 지름 [m]
k	풀리 수 [-]
P	전달할 동력 [N]
v	벨트 속도 [m/s]
F c	원심력 [N]
F 1	주어진 풀리에 대한 입력 시 벨트 스팬의 장력 [-]
F 2	주어진 풀리에 대한 출력 시 벨트 스팬의 장력 [-]
f	주어진 풀리의 수정된 마찰계수 [-]
P x	주어진 풀리의 동력비 [-]
f g	주어진 풀리 재질 및 벨트의 마찰계수 [-]
f mod	마찰 수정의 속도 계수 [s/m]
Z	벨트 수 [-]
ρ	벨트 밀도 [kg/m3]
F t	벨트 초기 장착 장력 [N
F v	주어진 풀리의 정적 인장 조정 힘 [N]
k 1	벨트 인장 계수 [-]

주: i - 풀리 지수