완전 유체 윤활은 마멸이 크지 않으면서 안정적인 서비스를 보장하므로 유체 윤활 베어링을 가장 중요한 평면 베어링 유형이라고 할 수 있습니다. 슬라이딩 표면의 상대적 운동에 의해 이 베어링의 윤활층이 생성됩니다. 이 운동을 통해 윤활제 점착력으로 인해 윤활제가 윤활 슬롯에 주입됩니다. 지지 층은 좁은 V 모양 슬롯에서 발생합니다. 이 층에서는 유체 압력 필드가 작성되며 베어링 하중력과 균형을 유지해야 하는 힘이 발생합니다. 유체 역학 압력 필드는 다음의 베어링 도식도에 표시되어 있습니다.
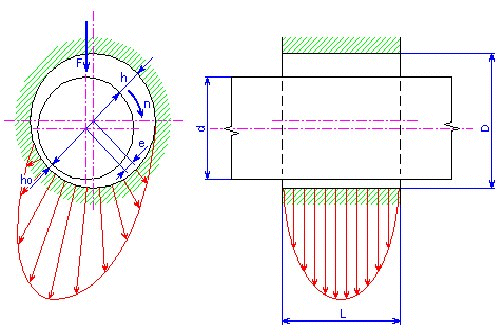
사용된 변수의 의미:
|
d |
저널 베어링 지름 [mm] |
|
D |
베어링 지름 [mm] |
|
e |
베어링의 저널 베어링 편심 [μm] |
|
F |
하중력 [N] |
|
h o |
베어링 작동 중 유체 효과 윤활층의 최소 두께 [μm] |
|
L |
베어링 폭 [mm] |
|
n |
저널 베어링 속도 [min -1 ] |
윤활층의 두께는 슬라이딩 표면의 상대적 운동 속도(베어링 저널의 속도), 윤활제 점도 및 활성 하중력에 따라 달라집니다. 기계 부품의 슬라이딩 표면이 결코 완벽하게 부드럽거나 고르지 않기 때문에 완전한 분리 및 연속 액체 마찰이 생성을 위한 최소 슬라이딩 속도가 필요한 특정 최소 두께의 윤활층을 보장합니다. 이 속도에 도달하지 않으면 베어링은 최소 마찰 조건에서 작동합니다.
유체 지지층에서의 흐름은 대부분의 베어링에서는 편형이 됩니다. 슬라이딩 속도가 높은 경우에만 난류가 생성될 수 있습니다. 저널 속도가 높은 경우 속도 주파수가 반으로 줄어든 소용돌이 진동이 발생하기도 합니다. 이 조건을 방지하려면 베어링을 검사해야 합니다. 최소 마찰 한계에서 최소 속도뿐만 아니라 최대 속도 한계도 검사해야 합니다.
유체 반지름 평면 베어링의 계산은 베어링의 실제 설계 및 작업 조건을 고려한 레이놀드 방정식의 해에 기반합니다. 레이놀드 방정식을 풀기 위해 다음과 같은 많은 단순화 조건이 사용됩니다.
- 윤활 액체는 압축할 수 없으며 흐름 속도도 일반적인 속도 한계보다 훨씬 더 낮습니다.
- 흐름이 일정하고 얇고 등온이며, 윤활 액체의 밀도, 점도 및 온도는 어디에서나 항상 일정합니다.
- 제한 윤활층은 슬라이딩 표면의 전송 속도로 이동합니다.
- 윤활층이 얇아서 곡률의 영향을 생략할 수 있으며 직선 방향으로 계산하여 층을 풀 수 있습니다.
- 윤활층은 특성이 동일한 윤활제에 의해 완전히 채워집니다.
- 윤활제 중량과 윤활층의 관성력은 무시할 수 있습니다.
- 윤활제는 이 방향의 일정한 압력으로 인해 윤활층 두께 방향으로 흐르지 않습니다.
- 윤활 압력 필드에 미치는 입력 압력의 영향 및 윤활층의 음압 부분의 영향은 고려하지 않습니다.
- 슬라이딩 표면 형태의 미시적 및 거시적 기하 편차는 해당하는 이상적인 형상 형태로 변환되며 상호 위치의 편차는 무시됩니다.
- 베어링 부품은 이상적으로 단단하지만 크기와 모양을 변경하지는 않습니다.
- 베어링 출력의 평균 윤활제 온도는 계산을 위해 윤활제 점성을 결정하는 지배적인 온도로 고려됩니다.
베어링 부품은 강성이 아니며 생산, 조립 및 작동으로 인해 이상적인 형태나 상호 위치가 없기 때문에 이러한 가정이 어느 정도 충족되는지 고려해야 합니다. 주로 온도 변화로 인한 윤활제 점성 또는 심지어 밀도의 변화로 인해 계산 및 실제 베어링 특성의 차이가 생길 수 있습니다. 공기 및 먼지가 윤활 액체와 함께 윤활층으로 들어가면 베어링 기능이 상당한 영향을 받을 수 있습니다.