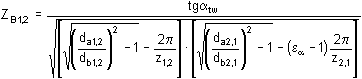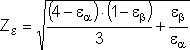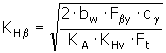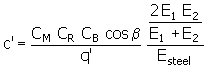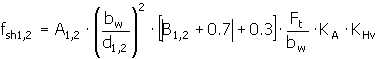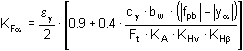Obliczenia wytrzymałości przekładni walcowej według CSN 01 4686, ISO 6336 i DIN 3990

Oparte na obliczeniach belki o ustalonych zakończeniach. Uwzględniają większość czynników.

Współczynniki bezpieczeństwa

Zmęczenie kontaktowe

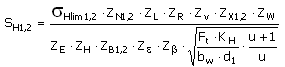
gdzie:

	σ Hlim	kontaktowa wytrzymałość zmęczeniowa (właściwość materiału)
	F t	siła styczna działająca na zęby
	b w	robocza szerokość wieńca
	d 1	średnica podziałowa zębnika

Kontakt przy obciążeniu jednorazowym

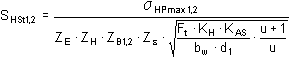
gdzie:

	σ HPmax	dopuszczalne naprężenie kontaktowe
	K AS	współczynnik przeciążenia jednorazowego

Zmęczenie przy zginaniu

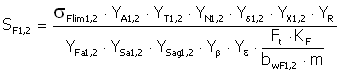
gdzie:

	σ Flim	granica zmęczenia dla zginania (właściwość materiału)
	b wF1,2 = min (b 1,2 , b w + 2m)	szerokość zęba dla zginania

Zginanie przy obciążeniu jednorazowym

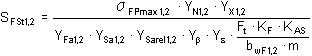
gdzie:

σ FPmax

dopuszczalne naprężenie zginające

Obliczenia współczynników

Z _N ... współczynnik trwałości (dla kontaktu)

1 ≤ Z _N ≤ 1.3 dla stali azotowanych

1 ≤ Z _N ≤ 1.6 dla pozostałych stali

	N Hlim	podstawowa liczba cykli obciążenia dla kontaktu (właściwość materiału)
	N K1,2 = 60 L h n 1,2	wymagana liczba cykli obciążenia (prędkość)

Y _N ... współczynnik trwałości (dla zginania)

1 ≤ Y _N ≤ 1.6 dla stali azotowanych

1 ≤ Y _N ≤ 2.5 dla pozostałych stali

	N Flim	podstawowa liczba cykli obciążenia dla zginania (właściwość materiału)
	N K1,2 = 60 L h n 1,2	wymagana liczba cykli obciążenia (prędkość)

Z _L ... współczynnik smarowania

	DIN i ISO:
		Z L = C ZL + 4 (1 - C ZL ) 0,158
		C ZL = σ Hlim / 4375 + 0,6357
		dla σ Hlim < 850 Mpa C ZL = 0,83
		dla σ Hlim < 1200 Mpa C ZL = 0,91

Z _R ... współczynnik chropowatości

Z _V ... współczynnik prędkości

	CSN:
		Z v = 0,95 + 0,08 log v
	ISO i DIN:
		C ZV = C ZL + 0,02

Z _E ... współczynnik sprężystości

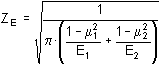
gdzie:

	μ	współczynnik Poissona (właściwość materiału)
	E	moduł sprężystości (właściwość materiału)

Z _H ... współczynnik współpracujących zębów

Z _B ... współczynnik zazębienia jednoparowego

dla ε≥ 1 lub wewnętrznej przekładni:
	Z B1,2 = 1
dla ε = 0:
dla ε < 1:
	Z B1,2 = Z B0 - ε b (Z B0 - 1) gdzie:
	Z B0 = Z B1,2 obliczono dla ε = 0

Z ε ... współczynnik liczby przyporu

dla ε = 0:
dla ε < 1:
dla ε≥ 1:

Y ... współczynnik liczby przyporu (dla zginania)

CSN:

	dla ε < 1:
	dla ε≥ 1:

ISO i DIN:

Z ... współczynnik kąta pochylenia zęba (dla kontaktu)

CSN:

Z = 1

ISO i DIN:

Y ... współczynnik kąta pochylenia zęba (dla zginania)

CSN:

Y βmin = 1 - 0.25 ε≥ 0.75

ISO i DIN:

	dla ε > 1 zastosowano ε = 1
	dla β > 30° zastosowano β = 30°

Z _x ... współczynnik wielkości (dla kontaktu)

Y _x ... współczynnik wielkości (dla zginania)

Z _W ... współczynnik twardości roboczej

Y _Fa ... współczynnik kształtu

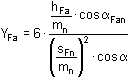
gdzie:

	h Fa	ramię zginające siły działającej na zakończenie zęba
	s Fn	grubość niebezpiecznego przekroju podstawy zęba koła pomocniczego
	α Fan	kąt zginania na końcu prostego zęba koła pomocniczego

Y _Sa ... współczynnik korekcyjny naprężenia

Y _Sa = (1,2 + 0,13 L _a ) q _s ^exp

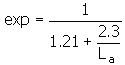
Y _Sag ... współczynnik dodatkowego karbu w podstawie zębów

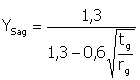
Y ... współczynnik wrażliwości na działanie karbu (zależy od materiału i promienia krzywizny przekształcenia stopy zęba)

Y _R ... współczynnik powierzchni stopy zęba

K _H ... współczynnik dodatkowego obciążenia (dla kontaktu)

K _H = K _A K _Hv K _Hb K _Ha

K _F ... współczynnik dodatkowego obciążenia (dla zginania)

K _F = K _A K _Fv K _Fb K _Fa

K _A ... współczynnik użytkowy (zewnętrznych sił dynamicznych)

K _Hv ... współczynnik użytkowy (wewnętrznych sił dynamicznych) dla kontaktu

K _Hv ... współczynnik użytkowy (wewnętrznych sił dynamicznych) dla zginania

dla CSN:

przy K A F t / b w < 150, uwzględniając K A F t / b w = 150

dla ISO i DIN:

	przy K A F t / b w < 100, uwzględniając K A F t / b w = 100
	gdzie: K P , K Q ... wartości tabeli

K _Hβ ... współczynnik obciążenia podłużnego (dla kontaktu)

dla CSN:

gdzie:

	c = 0,4	koła z utwardzanymi bokami zęba
	c = 0,3	nieutwardzane koła zębate
	f ky = | f sh1 + f sh2 | + f kZ - y
	f b , f x , f y ... tolerancja zębów y ... wartość tabeli

dla ISO i DIN:

	dla
	w innym przypadku ( < 1):
	F βy = F βx χ
	dla kół z utwardzanymi bokami zębów χ = 0,85
	dla pozostałych
	F βx = 1.33 f sh + f ma

	q' = 0,04723 + 0,15551/z v1 + 0,25791/z v2 - 0,00635 x 1 - 0,11654 x 1 /z v1 - 0,00193 x 2 - 0,24188 x 2 /z v2 + 0,00529 x 1 2 + 0,00182 x 2 2
	dla F t K A / b w < 100 wartości te są interpolowane
	dla ISO c' = c' [(F t K A / b w ) / 100] 0,25
	dla DIN c' = c' (F t K A / b w ) / 100
	C M = 0,8
	C R = 1 dla stałych przekładni
	C B = [1 + 0,5 (1,2 - h f /m)] [1 - 0,02 (20° - α)]
	E stal = 206 000
	c = c' (0,75 ε + 0,25)
	A, B ... wartości tabeli zależne od rozmieszczenia kół zębatych, wałków i łożysk

K _Fβ ... współczynnik obciążenia podłużnego (dla zginania)

K _Fβ = (K _Hβ ) ^NF

gdzie:

	h = 2 m/ε	przekładnia walcowa
	h = 2 m	przekładnia zębata skośna

K _Fa współczynnik obciążenia poprzecznego (dla zginania)

dla ε < 2:
dlaε > 2:
	przy K A F t / b w < 100 uwzględniając K A F t / b w = 100
wartości graniczne:
	dla CSN: 1 ≤ K Fα ≤ε

K _Hα ... współczynnik obciążenia poprzecznego (dla kontaktu)

dla CSN:
	K Hα = 1 dla zęba prostego
	K Hα = K Fα dla zęba pochyłego
DIN i ISO:
	K Hα = K Fα
dla wartości granicznych: