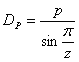Długość łańcucha jest określona liczbą ogniw łańcucha oraz podział łańcucha. Trajektoria napędu łańcucha oparta jest na konkretnej pozycji koła i żądanym kierunku ruchu.
Algorytm obliczania długości łańcucha wykorzystuje średnice podziałowe kół. Średnica podziałowa dla każdego koła napędowego łańcucha rolkowego lub koła pośredniego jest uzyskiwana z poniższych równań.
Pozycja koła przesuwnego jest dostosowana, tak aby uzyskać żądaną długość łańcucha. Aby odnaleźć odpowiednią pozycję koła przesuwnego, w obliczeniach używana jest algebra liniowa i rozwiązanie iteracji.
Podczas obliczania długości łańcucha uwzględniany jest fakt, iż trajektoria złożona jest z segmentów liniowych o długości podziału łańcucha, a łuki są zamienane na rzeczywiste wieloboki.
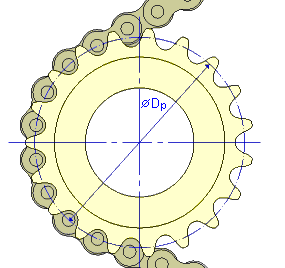
Średnice podziałowe
 |
|
|
|
gdzie: |
||
|
D P |
Średnica podziałowa |
|
|
p |
podział łańcucha |
|
|
z |
liczba zębów koła |
|
|
|
D p = D + D r |
|
|
gdzie: |
||
|
D P |
Średnica podziałowa |
|
|
D |
Nominalna średnica koła pośredniczącego |
|
|
D r |
maksymalna średnica rolki łańcucha |
|
Przykład napędu łańcucha z dwoma kołami
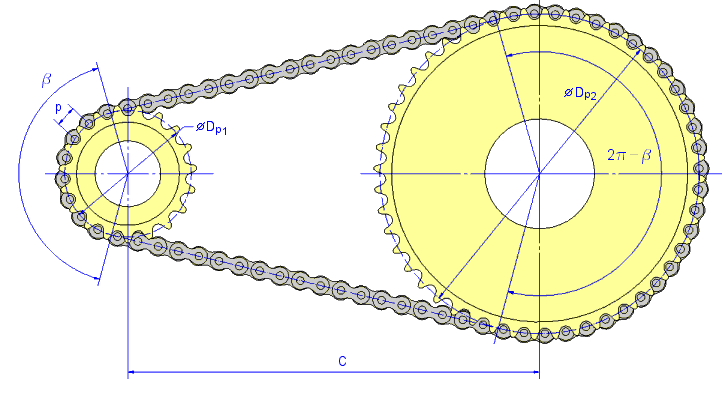
Wymagana liczba ogniw dla żądanej odległości osi

Wymagana liczba ogniw jest zaokrąglana do najbliższej liczby parzystej lub nieparzystej, a następnie rzeczywista odległość osi jest wyznaczana jako
C = F p [ 2 X - (z 1 + z 2 )]
gdzie:
|
|
|
|
|
Kąt działania jest wyznaczany jako
|
|
Liczba zębów w kontakcie z małym kołem
|
|
Znaczenie użytych zmiennych:
|
C 0 |
Wymagana odległość osi [m] |
|
C |
Rzeczywista odległość osi [m] |
|
p |
Podział łańcucha [m] |
|
z 1 |
Liczba zębów koła napędowego [-] |
|
z 2 |
Liczba zębów koła napędzanego [-] |
|
D P1 |
Średnica podziałowa koła napędowego [m] |
|
D P2 |
Średnica podziałowa koła napędzanego [m] |
|
X 0 |
Wymagana liczba ogniw łańcucha [-] |
| β |
Kąt działania [st] |