Ta sekcja zawiera listę problemów z weryfikacją w przypadku Generatora kształtów. Jeśli to możliwe, jest ważne porównanie Generatora kształtów ze znanymi lub teoretycznymi rozwiązaniami, aby zrozumieć, w jakich sytuacjach sprawdza się on niezawodnie.
Most
W tym problemie celem jest określenie konstrukcji potrzebnej do podparcia równomiernie rozłożonego obciążenia działającego na powierzchnię. Jak pokazano na ilustracji poniżej, istnieją trzy wiązania nieruchome na dole konstrukcji [1].
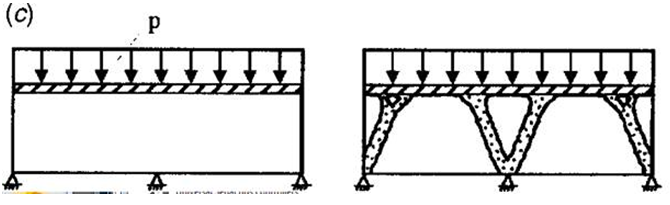
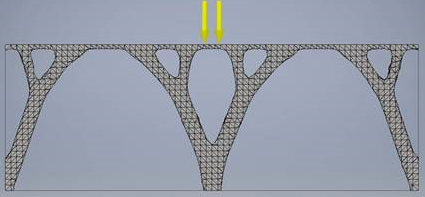
Za pomocą Generatora kształtów modelujemy tę konstrukcję jako belkę z równomiernie rozłożonym obciążeniem zastosowanym do górnej powierzchni. Trzy wiązania nieruchome są stosowane u dołu belki, po jednym na każdym końcu i jedno w środku. Wynik poniżej odpowiada w dużym stopniu opublikowanemu rozwiązaniu. Wygenerowany kształt ma postać mostu opartego na dwóch łukach, które przenoszą obciążenie ściskające na wiązania nieruchome.
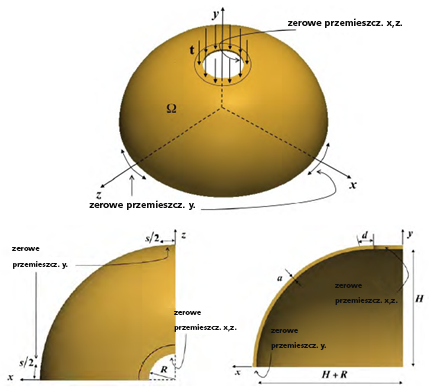
Półkulista skorupa
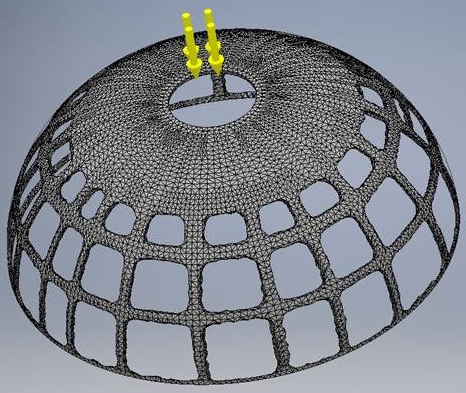
Ten problem polega na analizie cienkiej, półkulistej skorupy. Skorupa ma otwór na górze, wokół którego zastosowane jest obciążenie naciskiem. Przemieszczenia w osi y są zablokowane na dolnej krawędzi półkuli. Przemieszczenia na osi x i z są zablokowane wokół otworu w górnej części półkuli [2].
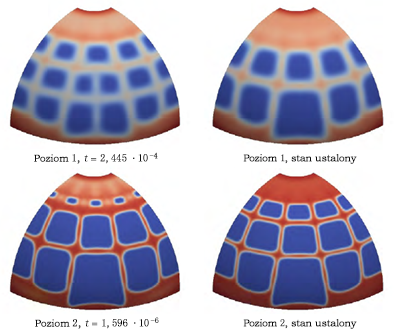

Za pomocą Generatora kształtów jesteśmy w stanie odtworzyć opublikowany wynik. Mimo iż znaczna część wyników zgadza się z opublikowanymi, na dolnej krawędzi półkuli występują pewne istotne różnice. W wyniku uzyskanym w Generatorze kształtów pozostaje tylko cienka warstwa materiału w miejscu, gdzie stosowane są warunki graniczne. Opublikowane wyniki wskazują znacznie szersze pasmo materiału wokół dolnej krawędzi półkuli. Opublikowane wyniki również wskazują pewne różnice w grubości pasma materiału, prawdopodobnie w wyniku zastosowania symetrii warunków obwiedni.
Odniesienia
- H. A. Eschenauer i N. Olhoff (2001) „Topology Optimization of Continuum Structures”, Journal of Applied Mechanics Reviews. 54(4): 372.
- L. Dede, M. J. Borden i T. J. R. Hughes (2012) „Isogeometric Analysis for Topology Optimization with a Phase Field Model”, Archives of Computational Methods in Engineering. 19(3): 427–465.