Obliczenia sprężyn skrętowych w przypadku jednostek metrycznych

Ogólne wzory obliczeń

Średnica zewnętrzna sprężyny

D ₁ = D + d [mm]

gdzie:

	D	średnica podziałowa sprężyny [mm]
	d	średnica drutu [mm]

Średnica wewnętrzna sprężyny

D ₂ = D - d [mm]

gdzie:

	D	średnica podziałowa sprężyny [mm]
	d	średnica drutu [mm]

Moment obrotowy dla wstępnie obciążonej sprężyny

gdzie:

	F 1	siła robocza, dla sprężyny wstępnie obciążonej [N]
	R 1	ramię siły roboczej [mm]

Moment obrotowy dla w pełni obciążonej sprężyny

gdzie:

	F 8	siła robocza (dla całkowicie obciążonej sprężyny) [N]
	R 1	ramię siły roboczej [mm]

Wskaźnik sprężyny

c = D/d [-]

gdzie:

	D	średnica podziałowa sprężyny [mm]
	d	średnica drutu [mm]

Kąt skoku roboczego

ϕ _h = ϕ ₈ - ϕ ₁ [°]

gdzie:

	ϕ 8	ugięcie kątowe ramienia roboczego dla całkowicie obciążonej sprężyny [°]
	ϕ 1	ugięcie kątowe ramienia roboczego dla stanu wstępnego obciążenia [°]

Minimalne ugięcie kątowe ramienia roboczego

gdzie:

	M 1	Moment obrotowy dla wstępnie obciążonej sprężyny [Nm]
	k	sztywność kątowa sprężyny [Nm/°]
	ϕ h	kąt skoku roboczego [°]
	M 8	skręt dla sprężyny w pełni obciążonej [Nm]

Maksymalne ugięcie kątowe ramienia roboczego

gdzie:

	M 1	Moment obrotowy dla wstępnie obciążonej sprężyny [Nm]
	k	sztywność kątowa sprężyny [Nm/°]
	ϕ h	kąt skoku roboczego [°]
	M 8	skręt dla sprężyny w pełni obciążonej [Nm]

Współczynnik koncentracji naprężeń

gdzie:

	i	Wskaźnik sprężyny [-]
	i = D/d [-]	dla obliczeń naprężenia zginającego w czynnych zwojach
		dla obliczeń naprężenia w zgięciu ramienia
	r	promień zginania w ramieniu (wewnętrzny) [mm]
	d	średnica drutu [mm]

Naprężenie materiału sprężyny, ogólnie

gdzie:

	M	skręt dla sprężyny, ogólnie [Nm]
	K f	współczynnik koncentracji naprężeń [-]
	d	średnica drutu [mm]

Liczba aktywnych zwojów sprężyny

gdzie:

	ϕ	ugięcie kątowe ramienia roboczego, ogólnie [°]
	E	moduł sprężystości [psi]
	d	średnica drutu [mm]
	M	skręt dla sprężyny, ogólnie [Nm]
	R 1	ramię siły roboczej [mm]
	R 2	ramię siły reakcji [mm]
	D	średnica podziałowa sprężyny [mm]

Obliczenia projektu sprężyny

Podczas projektowania sprężyny, średnica drutu, ilość zwojów i średnica gięcia ramienia ucha zginania są zaprojektowane w ten sposób, aby odpowiadały określonemu obciążeniu, materiałowi i wymiarom zespołu. Zaprojektuj sprężynę w ten sposób, aby odpowiadała ona żądanym średnicom drutu. Dla sprężyn o luzie między zwojami podział t między gwintami sprężyny w stanie bez obciążenia musi być z przedziału 0,3 D≤ t ≤ 0,5 D [mm]

Projekt sprężyny jest oparty na warunku wytrzymałości (σ ₈ ≤ u _s sA) i (σ _8r ≤ u _s σ _A ) i zalecanych przedziałach niektórych wymiarów geometrycznych sprężyny.

L _Z ≤ 10 D i L _Z ≤ 31.5 cala i 4 ≤ D/d ≤ X i n≥ 1.5 i 1.2 d ≤ t < D i r ≥ d.

gdzie:

• Sprężyna ze zwojami przylegającymi X = 16
• Sprężyna z luzem pomiędzy zwojami X = 10

Wymiary sprężyny odpowiadają rzeczywistemu rozwiązaniu geometrycznemu zgodnie z określonym kształtem i długością ramion. Jeśli określone w specyfikacji, wymiary muszą odpowiadać wymiarom montażowym granicznym, które stanowią maksymalna dozwolona średnica otworu i długość lub maksymalna dozwolona średnica pręta).

Określone maksymalne obciążenie, materiał i wymiary zespołu sprężyny

Najpierw obliczane i sprawdzane są wartości wejściowe dla obliczeń.

Następnie obliczane jest minimalne obciążenie dla określonego maksymalnego obciążenia i wymiarów zespołu.

gdzie:

	M 1	Moment obrotowy dla wstępnie obciążonej sprężyny [Nm]
	M 8	skręt dla sprężyny w pełni obciążonej [Nm]
	ϕ 1	ugięcie kątowe ramienia roboczego dla stanu wstępnego obciążenia [°]
	ϕ 8	ugięcie kątowe ramienia roboczego dla całkowicie obciążonej sprężyny [°]

Pod koniec zadania projektowane są średnica drutu i liczba zwojów, tak aby po obliczeniu średnicy sprężyny warunki wytrzymałościowe i geometryczne były spełnione. Jeśli wartość średnicy sprężyny jest ograniczona w specyfikacji, projekt sprężyny musi jej odpowiadać. Jeśli ograniczenie w specyfikacji nie jest określone, ograniczenia średnicy sprężyny są określone przez warunki geometryczne dla minimalnej i maksymalnej możliwej średnicy drutu.

Dla sprężyn o ramionach zagiętych projektowane są odpowiednie promienie gięcia na ramieniu.

Wszystkie średnice drutu sprężyny o określonej wytrzymałości i warunkach geometrycznych są obliczane, poczynając od najmniejszej średnicy drutu do największej. Następnie testowana jest podatność z wszystkimi wymaganymi warunkami na odpowiednią liczbę zwojów. Jeśli wszystkie warunki są spełnione, projekt jest skończony z wybranymi wartościami, bez względu na możliwe pozostałe średnice drutu sprężyny, a sprężyna jest zaprojektowana z najmniejszą możliwą średnicą drutu, najmniejszą liczbą zwojów i najmniejszymi średnicami sprężyny.

Określone obciążenie, materiał i kąt ugięcia roboczego

Najpierw sprawdzane są wartości wejściowe dla obliczeń.

Dla określonego obciążenia i kąta odchylenia roboczego są następnie obliczane ugięcia kątowe ramienia roboczego.

Minimalne ugięcie ramienia roboczego

Maksymalne ugięcie ramienia roboczego

gdzie:

	M 1	Moment obrotowy dla wstępnie obciążonej sprężyny [Nm]
	M 8	skręt dla sprężyny w pełni obciążonej [Nm]
	ϕ 1	ugięcie kątowe ramienia roboczego dla stanu wstępnego obciążenia [°]
	ϕ 8	ugięcie kątowe ramienia roboczego dla całkowicie obciążonej sprężyny [°]
	ϕ h	kąt skoku roboczego [°]

Następnie projektowane są średnica drutu i liczba zwojów, tak aby po obliczeniu średnicy sprężyny spełnione były wymagane warunki wytrzymałościowe i geometryczne. Jeśli wartość średnicy sprężyny jest ograniczona w specyfikacji, projekt sprężyny musi odpowiadać warunkom specyfikacji. W przeciwnym przypadku, ograniczenia średnicy sprężyny są określone przez warunki geometryczne dla minimalnej i maksymalnej możliwej średnicy drutu.

Dla sprężyn o ramionach zagiętych projektowane są odpowiednie promienie gięcia na ramieniu.

Wszystkie średnice drutu sprężyny o określonej wytrzymałości i warunkach geometrycznych są rozważane, poczynając od najmniejszej średnicy drutu do największej. Następnie testowana jest podatność z wymaganymi warunkami na odpowiednią liczbę zwojów. Jeśli wszystkie warunki są spełnione, projekt jest skończony z wybranymi wartościami, bez względu na możliwe pozostałe średnice drutu sprężyny, sprężyna jest zaprojektowana z najmniejszą możliwą średnicą drutu, najmniejszą liczbą zwojów i najmniejszymi średnicami sprężyny.

Określone maksymalne obciążenie, materiał i średnica sprężyny

Najpierw sprawdzane są wartości wejściowe dla obliczeń.

Następnie projektowane są średnica drutu, liczba zwojów i wymiary zespołu, tak aby spełnione były wymagane warunki wytrzymałościowe i geometryczne. Jeśli wartość kąta ugięcia roboczego jest ograniczona w specyfikacji, projekt sprężyny musi odpowiadać warunkom specyfikacji. Jeśli nie, ograniczenia wymiarów zespołu są określone przez warunki geometryczne dla określonej średnicy sprężyny oraz minimalnej i maksymalnej dopuszczalnej średnicy drutu.

Dla sprężyn o ramionach zagiętych, obliczane są odpowiednie promienie gięcia na ramieniu.

Wszystkie średnice drutu sprężyny o określonej wytrzymałości i warunkach geometrycznych są rozważane i obliczane są stosowne projekty z coraz większymi średnicami drutu, poczynając od najmniejszej średnicy do największej. Następnie testowana jest podatność z wymaganymi warunkami na liczbę zwojów. Jeśli wszystkie warunki są spełnione, projekt jest skończony z wybranymi wartościami, bez względu na możliwe pozostałe średnice drutu sprężyny, sprężyna jest zaprojektowana z najmniejszą możliwą średnicą drutu, najmniejszą liczbą zwojów i najmniejszymi średnicami sprężyny.

Określone maksymalne obciążenie, materiał, średnica sprężyny i kąt ugięcia roboczego

Najpierw sprawdzane są wartości wejściowe dla obliczeń.

Następnie optymalizowane są średnica, liczba zwojów i wychylenia kątowe ramienia roboczego, tak aby zachowana była wspomniana wcześniej wytrzymałość i warunki geometryczne. Program szuka minimalnego maksymalnego ugięcia ramienia roboczego ϕ ₈ biorąc pod uwagę wymaganie, aby minimalne ugięcie ramienia roboczego ϕ ₁ wynosiło około 2°.

Dla sprężyn o ramionach zagiętych obliczane są odpowiednie promienie gięcia na ramieniu.

Ostatecznie obliczane jest minimalne naprężenie sprężyny dla określonego maksymalnego obciążenia i ugięć kątowych ramienia roboczego.

gdzie:

	M 1	Moment obrotowy dla wstępnie obciążonej sprężyny [Nm]
	M 8	skręt dla sprężyny w pełni obciążonej [Nm]
	ϕ 1	ugięcie kątowe ramienia roboczego dla stanu wstępnego obciążenia [°]
	ϕ 8	ugięcie kątowe ramienia roboczego dla całkowicie obciążonej sprężyny [°]

Wszystkie średnice drutu sprężyny o określonej wytrzymałości i warunkach geometrycznych są rozważane i obliczane są stosowne projekty z coraz większymi średnicami drutu, poczynając od najmniejszej średnicy do największej. Testowana jest podatność z wszystkimi wymaganymi warunkami na ilość zwojów. Jeśli wszystkie warunki są spełnione, projekt jest skończony z wybranymi wartościami, bez względu na możliwe pozostałe średnice drutu sprężyny, sprężyna jest zaprojektowana z najmniejszą możliwą średnicą drutu, najmniejszą liczbą zwojów i najmniejszymi średnicami sprężyny.

Obliczenia sprawdzające sprężyny

Obliczane są odpowiednie wartości wymiarów zespołu dla określonego obciążenia, materiału i wymiarów sprężyny. Najpierw obliczane i sprawdzane są dane wejściowe, następnie obliczane są wymiary zespołu przy użyciu następujących wzorów.

Minimalne ugięcie kątowe ramienia roboczego

gdzie:

	M 1	Moment obrotowy dla wstępnie obciążonej sprężyny [Nm]
	D	średnica podziałowa sprężyny [mm]
	n	liczba czynnych zwojów [-]
	R 1	ramię siły roboczej [mm]
	R 2	ramię siły reakcji [mm]
	E	moduł sprężystości materiału [MPa]
	d	średnica drutu [mm]

Maksymalne ugięcie kątowe ramienia roboczego

gdzie:

	M 8	skręt dla sprężyny w pełni obciążonej [Nm]
	D	średnica podziałowa sprężyny [mm]
	n	liczba czynnych zwojów [-]
	R 1	ramię siły roboczej [mm]
	R 2	ramię siły reakcji [mm]
	E	moduł sprężystości materiału [MPa]
	d	średnica drutu [mm]

Kąt skoku roboczego

ϕ _h = ϕ ₈ - ϕ ₁ [°]

gdzie:

M 8	skręt dla sprężyny w pełni obciążonej [Nm]
ϕ 8	ugięcie kątowe ramienia roboczego dla całkowicie obciążonej sprężyny [°]

Obliczenia sił roboczych

Obliczane są siły wytworzone przez sprężynę w jej stanach roboczych dla określonego materiału, wymiarów zespołu i wymiarów sprężyny. Dane wejściowe są obliczane i sprawdzane, a następnie obliczane są wymiary zespołu przy użyciu następujących wzorów.

Minimalne obciążenie robocze

gdzie:

	M 1	Moment obrotowy dla wstępnie obciążonej sprężyny [Nm]
	D	średnica podziałowa sprężyny [mm]
	n	liczba czynnych zwojów [-]
	R 1	ramię siły roboczej [mm]
	R 2	ramię siły reakcji [mm]
	E	moduł sprężystości materiału [MPa]
	d	średnica drutu [mm]
	ϕ 1	ugięcie kątowe ramienia roboczego dla stanu wstępnego obciążenia [°]

Maksymalna siła robocza

gdzie:

	M 8	skręt dla sprężyny w pełni obciążonej [Nm]
	D	średnica podziałowa sprężyny [mm]
	n	liczba czynnych zwojów [-]
	R 1	ramię siły roboczej [mm]
	R 2	ramię siły reakcji [mm]
	E	moduł sprężystości materiału [MPa]
	d	średnica drutu [mm]
	ϕ 8	ugięcie kątowe ramienia roboczego dla całkowicie obciążonej sprężyny [°]

Obliczenia parametrów wyjściowych sprężyny

Wspólne dla wszystkich typów obliczeń sprężyny i obliczane w następującym porządku.

Sztywność kątowa sprężyny

Odstęp między zwojami dla luźnej sprężyny

a = t - d [mm]

Długość zwiniętej części sprężyny dla sprężyny luźnej

dla sprężyny ze zwojami przylegającymi
	L 0 = (1,05 n + 1) d [mm]
dla sprężyny z luzem pomiędzy zwojami
	L 0 = t n + d [mm]

Naprężenie zginające materiału sprężyny w zwojach aktywnych dla minimalnego obciążenia roboczego

gdzie współczynnik koncentracji naprężeń K _f oblicza się dla i = D/d

Naprężenie zginające materiału sprężyny w miejscu gięcia na ramieniu dla minimalnego obciążenia roboczego

gdzie współczynnik koncentracji naprężeń K _f oblicza się dla i = 2r/d + 1

Naprężenie zginające materiału sprężyny w zwojach aktywnych dla stanu pełnego obciążenia

gdzie współczynnik koncentracji naprężeń K _f oblicza się dla i = D/d

Naprężenie zginające materiału sprężyny w miejscu gięcia na ramieniu dla stanu pełnego obciążenia

gdzie współczynnik koncentracji naprężeń K _f oblicza się dla i = 2r/d + 1

Długość zwiniętej części sprężyny w stanie pełnego obciążenia dla sprężyny ze zwojami przylegającymi i o obciążeniu w kierunku zwijania

Średnica zewnętrzna sprężyny w stanie pełnego obciążenia i obciążeniu w kierunku zwijania

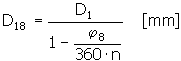
Średnica wewnętrzna sprężyny w stanie pełnego obciążenia i obciążeniu w kierunku zwijania

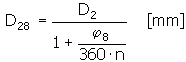
Graniczny próbny kąt ugięcia ramienia roboczego

Energia odkształcenia sprężyny

Długość drutu

l = 3,2 D n + l R [mm]
gdzie 1 R to długość ramienia, podczas gdy:
	gdzie 1 R to długość ramienia, podczas gdy:
			długość prostego ramienia stycznego
			długość ramienia wygiętego

Masa sprężyny

Sprawdzanie obciążenia sprężyny

(σ ₈ ≤ u _s σ _A ) i (σ _8r ≤ u _s σ _A )

Znaczenie użytych zmiennych:

a	luz między aktywnymi zwojami w stanie wolnym [mm]
d	średnica drutu [mm]
D	średnica podziałowa sprężyny [mm]
D 1	średnica zewnętrzna sprężyny [mm]
D 2	średnica wewnętrzna sprężyny [mm]
E	moduł sprężystości [psi]
F	siła robocza wywierana przez sprężynę (siła wywierana na ramieniu siły roboczej R 1 ), ogólnie [N]
i	wskaźnik sprężyny [-]
K F	współczynnik koncentracji naprężeń [-]
kϕ	sztywność kątowa sprężyny [Nm/°]
r 1	promień zginania ramienia roboczego [mm]
r 2	promień zginania ramienia oporowego [mm]
R 1	ramię siły roboczej [mm]
R 2 1	ramię siły reakcji [mm]
l	długość drutu [mm]
L 0	długość części sprężyny tworzonej zwojami w stanie luźnym, ogólnie [mm]
m	masa sprężyny [N]
M	skręt dla sprężyny, ogólnie [Nm]
n	liczba czynnych zwojów [-]
t	podział uzwojenia w stanie luźnym [mm]
u s	współczynnik wykorzystania materiału
ρ	gęstość materiału sprężyny [funt/stopa3]
ϕ	ugięcie kątowe ramienia roboczego, ogólnie [°]
σ	naprężenie zginające materiału sprężyny, ogólnie [psi]
σ A	dopuszczalne naprężenie zginające materiału sprężyny [psi]
M 1	Moment obrotowy dla wstępnie obciążonej sprężyny [Nm]
M 8	skręt dla sprężyny w pełni obciążonej [Nm]
ϕ 8	ugięcie kątowe ramienia roboczego dla całkowicie obciążonej sprężyny [°]
ϕ 1	ugięcie kątowe ramienia roboczego dla stanu wstępnego obciążenia [°]
ϕ 8	ugięcie kątowe ramienia roboczego dla całkowicie obciążonej sprężyny [°]
ϕ h	ugięcie kątowe ramienia roboczego dla całkowicie obciążonej sprężyny [°]