Сплайн представляет собой гладкую кривую, проходящую через набор точек, которые влияют на форму кривой, или рядом с ним.
По умолчанию сплайн представляет собой сочетание сегментов кривых полиномов 3-й степени (также называемых кубическими). Эти кривые называются неоднородными рациональными B-сплайнами (NURBS), однако для простоты именуются сплайнами. Кубические сплайны являются наиболее распространенными и имитируют сплайны, созданные вручную с использованием гибких полос, форма которых зависит от плотности в точках ввода данных.
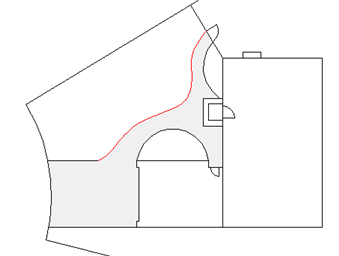
В следующем примере сплайн был использован для создания выделенной границы бетонного тротуара.
Описание управляющих вершин и определяющих точек
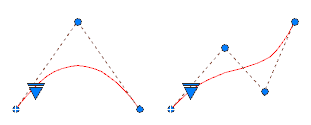
Сплайны можно создавать или редактировать с использованием управляющих вершин или определяющих точек. Для сплайна слева показаны управляющие вершины вдоль управляющего многоугольника, а для сплайна справа — определяющие точки.

С помощью треугольных ручек на выбранном сплайне можно переключить отображение управляющих вершин и определяющих точек. Можно использовать круглые и квадратные ручки для изменения выбранного сплайна.
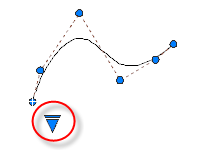
Создание сплайнов с помощью управляющих вершин
При создании сплайнов с помощью управляющих вершин между указанными точками отображаются временные линии, которые образуют управляющий многоугольник, задающий форму сплайна.
Этот метод дает прекрасную возможность изменять форму сплайна с помощью управляющих вершин . С помощью этого метода можно также указать полиномы более низкой или более высокой степени, включая степень 1 (линейный), степень 2 (квадратичный), степень 3 (кубический) и так далее вплоть до степени 10.
Создание сплайнов с помощью определяющих точек
При создании сплайнов с помощью определяющих точек результирующая кривая проходит через указанные точки и зависит от интервалов между математическими узлами кривой.
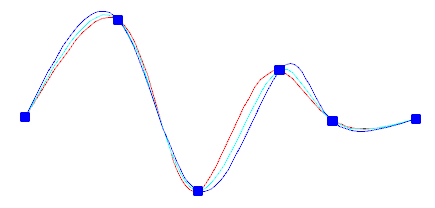
Можно выбрать интервал между этими узлами с помощью параметра узловой параметризации, в результате чего будут созданы другие кривые, как показано в примере.
Если для допуска задано значение 0, сплайн проходит непосредственно через определяющие точки. При более высоких значениях допуска сплайн проходит рядом с определяющими точками. Кроме того, можно указать направление касательной на каждом конце сплайна.
Особые случаи
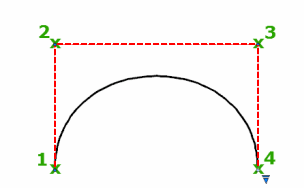
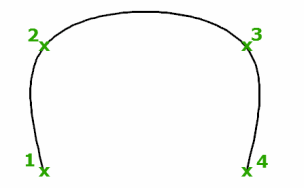
Можно создать сплайн параболической формы путем указания сплайна 2-й степени, созданного с помощью трех управляющих вершин, как показано на рисунке слева. Сплайны 3-степени, созданные с использованием четырех управляющих вершин, имеют такую же форму, что и кривые Безье 3-й степени, как показано на рисунке справа.