В этом разделе рассматриваются примеры форматов XML, используемых в различных методах отгона виража.
Пример стандартного метода отгона виража
В этом примере показан формат XML, используемый для вычисления пикетов перехода на двускатных дорогах без разделительной полосы по стандартной методике AASHTO:
<SuperelevationAttainmentMethod name="AASHTO 2001 - Crowned Roadway">
<AttainmentStyle style="Standard"/>
<TransitionFormula type="LCtoFS" formula="{t}"/>
<TransitionFormula type="LCtoBC" formula ="{p}*{t}"/>
<TransitionFormula type="NCtoLC" formula ="{t}*{c}/{e}"/>
<TransitionFormula type="LCtoRC" formula ="{t}*{c}/{e}"/>
<TransitionFormula type="NStoNC" formula ="{t}*({s}-{c})/{e}">
<SuperelevationAttainmentMethod>
Этот пример показывает определение метода отгона с именем "AASHTO 2001 - Двускатное дорожное полотно", в котором для отгона виража используется стандартный метод устранения нежелательного гребня. В пример включен расчет расстояния перехода, необходимое для устранения перелома обочины (тип="НОдоНП").
Пример метода отгона виража для односкатной дороги
В этом примере показана односкатная дорога без разделительной полосы. Дорога односкатная, поэтому операция устранения нежелательного гребня не применяется.
Для метода отгона односкатной дороги требуются две формулы: одна — для кривых, направление уклона которых противоположно направлению нормального поперечного уклона дороги, а другая — для кривых, у которых направление уклона виража совпадает с направлением нормального поперечного уклона дороги. На следующей иллюстрации показан нормализованный вираж с поперечным уклоном; дорога за пределами виража наклонена вниз слева направо. Поэтому для кривой слева требуется более длинный переход, чем для кривой справа.
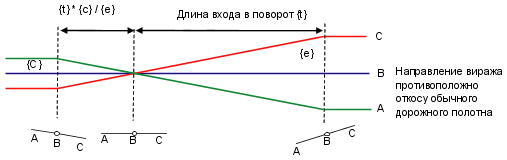
В следующем примере раздел "Continuing" (Совпадение направлений) определяет расстояние от нормального поперечного уклона до полного виража следующим образом: длина продолжения отгона {t} (рассчитывается по таблицам длин перехода) минус длина продолжения отгона, умноженная на нормальный поперечный уклон дорожного полотна {c} и деленная на уклон полного виража {e}. Вторая формула определяет расстояние от нормального поперечного уклона до начала кривой, как процент {t}, зависящий от переменной {p}, минус {c}, деленный на {e}.
Раздел "Opposing" (Встречный) определяет общее расстояние перехода как равное длине продолжения отгона {t}. Расстояние до начала кривой равно {p}*{t}, а расстояние между пикетами с нормальным поперечным уклоном и горизонтальной внешней полосой равно {t} * {c} / {e}.
<SuperelevationAttainmentMethod name="Undivided Planar Roadway">
<TransitionStyle style="Planar"/>
<Continuing>
<TransitionFormula type="NCtoFS" formula="{t}-{t}*{c}/{e}"/>
<TransitionFormula type="NCtoBC" formula="{t}*({p}-{c}/{e})"/>
</Continuing>
<Opposing>
<TransitionFormula type="LCtoFS" formula="{t}"/>
<TransitionFormula type="LCtoBC" formula="{p}*{t}"/>
<TransitionFormula type="NCtoLC" formula="{t}*{c}/{e}"/>
</Opposing>
<SuperelevationAttainmentMethod>
Переходы, определяемые шириной дороги и коэффициентом перехода
Не во всех организациях используются таблицы, из которых можно получить непосредственно длину перехода. В следующей таблице полный уклон виража и 
определяются как функция проектной скорости и радиуса кривизны. В данном случае значение используется для расчета длины перехода исходя из обычной ширины дороги. В таблицах значений длины перехода указаны не фактические значения длины, а значения .
| Радиус (м) | 90 км/ч | 100 км/ч | 110 км/ч | 120 км/ч | ||||
|---|---|---|---|---|---|---|---|---|
| E% |
|
E% |
|
E% |
|
E% | нет | |
| 7000 | NC | нет | NC | нет | NC | нет | NC | нет |
| 5000 | NC | нет | NC | нет | NC | нет | 2.0 | 0.31 |
| 3000 | 2.0 | 0.39 | 2.0 | 0.34 | 2.0 | 0.32 | 2.0 | 0.31 |
| 2500 | 2.0 | 0.39 | 2.0 | 0.34 | 2.0 | 0.32 | 2.0 | 0.31 |
| 2000 | 2.0 | 0.39 | 2.0 | 0.34 | 2.0 | 0.32 | 2.3 | 0.32 |
| 1500 | 2.0 | 0.39 | 2.0 | 0.34 | 2.2 | 0.33 | 3.0 | 0.33 |
| 1400 | 2.0 | 0.39 | 2.0 | 0.34 | 2.4 | 0.33 | 3.2 | 0.34 |
| 1300 | 2.0 | 0.39 | 2.0 | 0.34 | 2.6 | 0.33 | 3.5 | 0.34 |
| 1200 | 2.0 | 0.39 | 2.2 | 0.35 | 2.8 | 0.34 | 3.8 | 0.35 |
| 1000 | 2.0 | 0.39 | 2.6 | 0.36 | 3.7 | 0.35 | 4.5 | 0.37 |
| 900 | 2.2 | 0.40 | 2.9 | 0.37 | 3.7 | 0.36 | 5.0 | 0.38 |
| 800 | 2.5 | 0.40 | 3.3 | 0.38 | 4.2 | 0.38 | 5.7 | 0.39 |
| 700 | 2.9 | 0.41 | 3.7 | 0.39 | 4.8 | 0.39 | 6.0 | 0.40 |
| 600 | 3.4 | 0.42 | 4.4 | 0.41 | 5.6 | 0.41 | ||
| 500 | 4.0 | 0.44 | 5.2 | 0.43 | 6.0 | 0.42 | ||
| 400 | 5.0 | 0.46 | 6.0 | 0.45 | ||||
| 300 | 6.0 | 0.48 | ||||||
В следующем примере методы отгона и формулы для двух типов дорог используют таблицу, приведенную выше. Переменная {w} представляет собой обычную ширину дороги от точки вращения до края дороги и определяется с помощью Мастера создания виража.
<SuperelevationAttainmentMethod name="Unspiraled ramp">
<TransitionStyle style="Planar"/>
<Continuing>
<TransitionFormula type="NCtoFS" formula="100*{e}*{w}/{t}"/>
<TransitionFormula type="NCtoBC" formula="{p}*{e}*{w}/{t}"/>
</Continuing>
<Opposing>
<TransitionFormula type="LCtoFS" formula="100*{e}*{w}/{t}"/>
<TransitionFormula type="LCtoBC" formula="{p}*{e}*{w}/{t}"/>
<TransitionFormula type="NCtoLC" formula="100*{c}*{w}/{t}"/>
<TransitionFormula type="LCtoRC" formula="100*{c}*{w}/{t}"/>
</Opposing>
</SuperelevationAttainmentMethod>
<SuperelevationAttainmentMethod name="Unspiraled 2 way roadway">
<TransitionStyle style="Standard"/>
<TransitionFormula type="LCtoFS" formula="100*{e}*{w}/{t}"/>
<TransitionFormula type="LCtoBC" formula="{p}*{e}*{w}/{t}"/>
<TransitionFormula type="NCtoLC" formula="100*{c}*{w}/{t}"/>
<TransitionFormula type="LCtoRC" formula="100*{c}*{w}/{t}"/>
<SuperelevationAttainmentMethod>