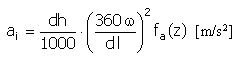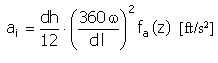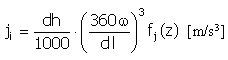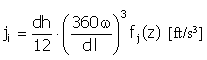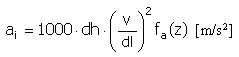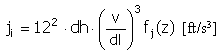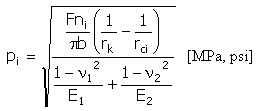Входные данные:
- Основной радиус r 0 (дисковые и цилиндрические кулачки)
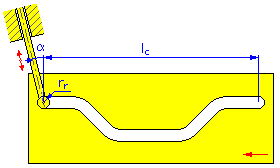
- Расстояние движения l c (Линейные кулачки)
- Ширина кулачка b c
- Радиус ролика r r
- Ширина цилиндра b r (для формы цилиндра толкателя)
- Эксцентриситет e (Дисковые кулачки для перемещения толкателя)
- Угол эксцентриситета α (Линейные и цилиндрические кулачки для перемещения толкателя)
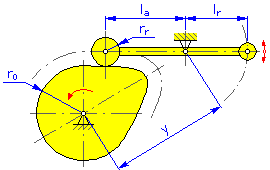
- Расстояние поворота y (Дисковые и линейные кулачки для поворотной руки)
- Длина локтя l a (Дисковые и линейные кулачки для поворотной руки)
- Реакция локтя l r (Дисковые и линейные кулачки для поворотной руки)
- Скорость ω(Дисковые и линейные кулачки)
- Скорость v (Линейные кулачки)
- Усилие на ролике F
- Вес элементов ускорения m
- Жесткость пружины c
- Допустимое давление p A1
- Модуль упругости материала кулачка E 1
- Коэффициент Пуассона материала кулачка μ 1
- Допустимое давление p A2
- Модуль упругости материала толкателя E 2
- Коэффициент Пуассона материала толкателя μ 2
|
Дисковый кулачок |
|
|
|
|
|
Линейный кулачок |
|
|
|
|
|
Цилиндрический кулачок |
|
 |
|
|
Внешний диаметр = 2r 0 +b c |
|
|
Внутренний диаметр = 2r 0 -b c |
|
Сегменты кулачка
- Функция движения f y (z) [бр]
- Обратное отношение k r (только для параболического движения и параболического с линейной деталью)
- Линейная деталь k l (только для параболического движения с линейной деталью)
- Начальное положение движения L 0 [°; мм, дюймы]
- Конечное положение движения L [°; мм, дюймы]
- Длина сегмента движения dL = L - L 0 [°; мм, дюймы]
- Подъем в начале h 0 [мм, дюймы]
- Подъем в конце h [мм, дюйм] макс. [мм, дюймы]
- Подъем сегмента d h = h - h макс. -h 0 [мм, дюймы]
Зависимости подъема
Дисковые и цилиндрические кулачки
Угол поворота кулачка ϕ i [°]
Фактическое относительное положение в сегменте: z i = (ϕ i - L 0 ) / dL (диапазон 0 - 1)
|
Подъем |
y i = dh f y (z) [мм, дюймы] |
|
Скорость |
|
|
|
|
|
Ускорение |
|
|
|
|
|
Импульс |
|
|
|
Линейный кулачок
Положение перемещения кулачка L i [мм, дюймы]
Фактическое относительное положение в сегменте: z i = (L i - L 0 ) / dL (диапазон 0 - 1)
|
Подъем |
y i = dh f y (z) [мм, дюймы] |
|
Скорость |
|
|
Ускорение |
|
|
|
|
|
Импульс |
|
|
|
Функции движения
Циклоидное (расширенное синусоидальное)
Это движение отличается превосходными характеристиками ускорения. Оно часто используется для высокоскоростных кулачков, поскольку отличается низким уровнем шума, вибрации и износа.

|
|
Подъем |
|
|
Скорость |
|
|
Ускорение |
|
|
Импульс |
|
Подъем |
f y (z) = z - 0,5/π sin(2πz) |
|
Скорость |
f v (z) = 1 - cos (2πz) |
|
Ускорение |
f a (z) = 2π sin(2πz) |
|
Импульс |
f j (z) = 4π 2 cos(2πz) |
Гармоническое (синусоидальные колебания)
Плавность характеристик скорости и ускорения во время хода является преимуществом данной кривой. Однако мгновенные изменения ускорения в начале и в конце движения могут вызывать вибрацию, шум и износ.

|
|
Подъем |
|
|
Скорость |
|
|
Ускорение |
|
|
Импульс |
|
Подъем |
f y (z) = 0,5 (1 - cos πz)) |
|
Скорость |
f v (z) = 0,5 π sin (πz) |
|
Ускорение |
f a (z) = 0,5 π 2 cos(πz) |
|
Импульс |
f j (z) = -0,5π 3 sin(πz) |
Линейное
Простое движение с резким ударом в начале и конце движения. Используется редко, за исключением очень грубых устройств. Рекомендуется использовать движение с измененным характером в начале и в конце - по параболе с линейным участком.

|
|
Подъем |
|
|
Скорость |
|
Подъем |
f y (z) = z |
|
Скорость |
f v (z) = 1 |
|
Ускорение |
f a (z) = 0 |
|
Прим.: Для z = 0 и z = 1 правильным значением должно быть бесконечное значение, однако оно недопустимо при расчете, поэтому используется нулевое значение.
|
|
|
Импульс |
f j (z) = 0 |
|
Прим.: Для z = 0 и z = 1 правильным значением должно быть бесконечное значение, однако оно недопустимо при расчете, поэтому используется нулевое значение.
|
Параболическое (полиноминальное второй степени)
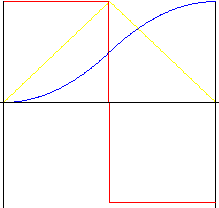
Движение минимально возможным ускорением. Однако вследствие резких изменений ускорения в начале, середине и конце движения создаются ударные воздействия. Коэффициент обратного направления обеспечивает "растяжение" в середине движения и допускает изменение коэффициента ускорения и торможения.
Зеркально отраженное (коэффициент обратного направления k r = 0.5)
|
|
Подъем |
|
|
Скорость |
|
|
Ускорение |
|
для z = от 0 до 0,5: |
|||
|
Подъем |
fy(z) = 2z 2 |
||
|
Скорость |
fv(z) = 4z |
||
|
Ускорение |
fa (z) = 4 |
||
|
Импульс |
fa(z) = 0 |
||
|
для z = от 0,5 до 1: |
|||
|
Подъем |
fy(z) = 1 - 2(1 - z) 2 |
||
|
Скорость |
fv(z) = 4 (1 - z) |
||
|
Ускорение |
fa (z) = -4 |
||
|
Импульс |
fj(z) = 0 |
||
|
Прим.: Для z = 0 и z = 1 правильным значением должно быть бесконечное значение, однако оно недопустимо при расчете, поэтому используется нулевое значение.
|
|||
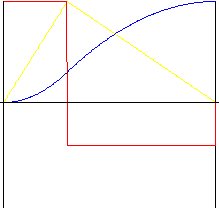
Незеркально отраженное
k r - коэффициент обратного направления (в диапазоне 0,01 - 0,99)
|
|
Подъем |
|
|
Скорость |
|
|
Ускорение |
|
для z = 0 до k r : |
|||
|
Подъем |
f y (z) = z 2 / k r |
||
|
Скорость |
f v (z) = 2z / k r |
||
|
Ускорение |
f a (z) = 2 / k r |
||
|
Импульс |
f j (z) = 0 |
||
|
для z = k r до 1: |
|||
|
Подъем |
f y (z) = 1 - (1 - z) 2 / (1 - k r ) |
||
|
Скорость |
f v (z) = 2 (1 - z) / (1 - k r ) |
||
|
Ускорение |
f a (z) = -2 / (1 - k r ) |
||
|
Импульс |
f j (z) = 0 |
||
|
Прим.: Для z = 0 и z = 1 правильным значением должно быть бесконечное значение, однако оно недопустимо при расчете, поэтому используется нулевое значение.
|
|||
По параболе с линейным участком
Обеспечивает более приемлемое ускорение и торможение по сравнению с линейным движением. Коэффициент обратного направления обеспечивает "растяжение" в середине движения и допускает изменение коэффициента ускорения и торможения. Коэффициент линейного участка позволяет задать относительный размер линейного участка движения.

|
|
Скорость |
|
|
Ускорение |
|
|
Импульс |
k r - коэффициент обратного направления (в диапазоне от 0,01 до 0,99)
k l - коэффициент линейного участка (в диапазоне от 0 до 0,99)
k z = 1 + k l / (1 - k l )
k h = (1 - k l ) / (1 + k l )
|
для z = 0 до k r / k z : |
|||
|
Подъем |
f y (z) = k h z 2 k z 2 / k r |
||
|
Скорость |
f v (z) = 2 k h z k z 2 / k r |
||
|
Ускорение |
f a (z) = 2 k h k z 2 / k r |
||
|
Импульс |
f j (z) = 0 |
||
|
для z = k r / k z до r / k z + k l : |
|||
|
Подъем |
f y (z) = (z - 0,5 k r / k z ) 2 / (1 + k l ) |
||
|
Скорость |
f v (z) = 2 / (1 + k l ) |
||
|
Ускорение |
f a (z) = 0 |
||
|
Импульс |
f j (z) = 0 |
||
|
для z = k r / k z + k l до 1: |
|||
|
Подъем |
f y (z) = 1 - k h (1 - z) 2 k z 2 / (1 - k r ) |
||
|
Скорость |
f v (z) = 2 k h (1 - z) k z 2 / (1 - k r ) |
||
|
Ускорение |
f a (z) = -2 k h k z 2 / (1 - k r ) |
||
|
Импульс |
f j (z) = 0 |
||
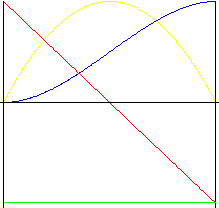
Полиномиальное третьей степени (кубическая парабола)
Движение с меньшими ударами, чем при движении по параболе.
|
|
Подъем |
|
|
Скорость |
|
|
Ускорение |
|
|
Импульс |
|
Подъем |
f y (z) = (3 -2z) z 2 |
|
Скорость |
f v (z) = (6 - 6z) z |
|
Ускорение |
f a (z) = 6 - 12z |
|
Импульс |
f j (z) = -12 |
Полиноминальное четвертой степени
Движение с меньшими ударами, чем при движении по траектории, описываемой полиномом 3-й степени.

|
|
Подъем |
|
|
Скорость |
|
|
Ускорение |
|
|
Импульс |
|
для z = 0 - 0,5 |
||
|
Подъем |
f y (z) = (1 - z) 8z 3 |
|
|
Скорость |
f v (z) = (24 - 32z) z 2 |
|
|
Ускорение |
f a (z) = (48 - 96z) z |
|
|
Импульс |
f j (z) = 48 - 192z |
|
|
для z = 0,5 - 1 |
||
|
Подъем |
f y (z) = 1 - 8z (1 - z) 3 |
|
|
Скорость |
f v (z) = (32z - 8) (1 - z) 2 |
|
|
Ускорение |
f a (z) = (48 - 96z) (1 - z) |
|
|
Импульс |
f j (z) = 194z - 144 |
|
Полиномиальное пятой степени
Движение с меньшими ударами, чем при движении по траектории, описываемой полиномом 3-й степени.

|
|
Подъем |
|
|
Скорость |
|
|
Ускорение |
|
|
Импульс |
|
Подъем |
f y (z) = (6z 2 - 15z + 10) z 3 |
|
Скорость |
f v (z) = (z 2 - 2z + 1) 30z 2 |
|
Ускорение |
f a (z) = (2z 2 - 3z + 1) 60z |
|
Импульс |
f j (z) = (6z 2 - 6z + 1) 60 |
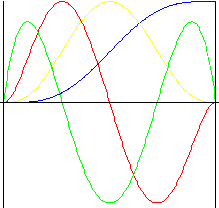
Полиномиальное седьмой степени
Гладкость во всех формулах, включающих импульс.
|
|
Подъем |
|
|
Скорость |
|
|
Ускорение |
|
|
Импульс |
|
Подъем |
f y (z) = (-20z 3 + 70z 2 - 84z + 35) z 4 |
|
Скорость |
f v (z) = (-z 3 + 3z 2 - 3z + 1) 140z 3 |
|
Ускорение |
f a (z) = (-2z 3 + 5z 2 - 4z + 1) 420z 2 |
|
Импульс |
f j (z) = (-5z 3 + 10z 2 - 6z + 1) 840z |
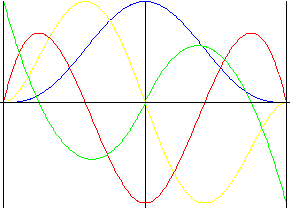
Незеркально отраженное полиноминальное пятой степени
Аналогично полиноминальному 5-й степени, но с принудительным движением вниз.
|
|
Подъем |
|
|
Скорость |
|
|
Ускорение |
|
|
Импульс |
|
Деталь 1 |
||
|
Подъем |
f y (z) = 1 - (8 (1 - z) 3 - 15 (1 - z) 2 + 10) (1 - z) 2 / 3 |
|
|
Скорость |
f v (z) = (2 (1 - z) 3 - 3 (1 - z) 2 + 1) (1 - z) 20 / 3 |
|
|
Ускорение |
f a (z) = -(8 (1 - z) 3 - 9 (1 - z) 2 + 1) 20 / 3 |
|
|
Импульс |
f j (z) = (4 (1 - z) 2 - 3 (1 - z)) 40 |
|
|
Часть 2 |
||
|
Подъем |
f y (z) = (8z 3 - 15z 2 + 10) z 2 / 3 |
|
|
Скорость |
f v (z) = (2z 3 - 3z 2 + 1) z 20/3 |
|
|
Ускорение |
f a (z) = (8z 3 - 9z 2 + 1) 20/3 |
|
|
Импульс |
f j (z) = (4z 2 - 3z) 40 |
|
Двойной гармоничный
Гладкость во всех формулах, включающих импульс с принудительным движением вниз.

|
Деталь 1 |
||
|
Подъем |
f y (z) = cos(0,5π (1 - z)) 4 |
|
|
Скорость |
f v (z) = π (0,5 sin(πz) - 0,25 sin(2πz)) |
|
|
Ускорение |
f a (z) = 0,5 π 2 (cos(πz) - cos(2πz)) |
|
|
Импульс |
f j (z) = π 3 (-0,5 sin(πz) + sin(2πz)) |
|
|
Часть 2 |
||
|
Подъем |
f y (z) = 1 - cos(0,5π z) 4 |
|
|
Скорость |
f v (z) = π (0,5 sin(πz) + 0,25 sin(2πz)) |
|
|
Ускорение |
f a (z) = 0,5 π 2 (cos(πz) + cos(2πz)) |
|
|
Импульс |
f j (z) = -π 3 (0,5 sin(πz) + sin(2πz)) |
|
Сравнение максимальных относительных значений
|
Движение |
Скорость |
Ускорение |
Импульс |
|
Циклоидный (расширенный синусоидальный) |
2 |
6.28 |
39.5 |
|
гармоническое (синусоидальные колебания) |
1.57 |
4.93 |
15.5 |
|
Единицы |
1 |
∞ |
∞ |
|
Параболическое (полиноминальное 2-й степени) |
2 |
4 |
∞ |
|
Полиноминальное 3-й степени |
1.5 |
6 |
12 |
|
Полиноминальное 4-й степени |
2 |
6 |
48 |
|
Полиномиальное 5-й степени |
1.88 |
5.77 |
60 |
|
Полиномиальное 7-й степени |
2.19 |
7.51 |
52.5 |
|
Незеркально отраженное полиноминальное 5-й степени |
1.73 |
6.67 |
40 |
|
Двойной гармоничный |
2.04 |
9.87 |
42.4 |
Другие зависимости
Усилие на ролике
|
F i = F + m a i + c y i [Н, фунт] |
Нормальная сила
|
Fn i = F i / cos (γ i ) [Н, фунт] |
Момент
|
T i = F i r i tan (γ i ) [Нмм, фунт дюйм] |
Удельное давление (Герц)
|
|
|
|
b = min (b v, b k ) |