Расчетная прочность на изгиб полностью составного сечения определяется в соответствии с разделом I3.2 норм ANSI/AISC 360-10. В процессе проектирования предполагается, что номинальный момент сопротивления сечения может быть рассчитан на основе распределения пластического напряжения на составном сечении для предельного состояния текучести (пластический момент). Это допущение применимо для всех стандартных W-форм в руководстве AISC, где F y < 50 кфунт/кв. дюйм.
При распределении пластического напряжения предполагается, что сталь является пластически деформируемой (при сжатии или растяжении), а напряжения в бетоне могут быть выражены эквивалентным блоком напряжения со значением интенсивности нагрузки 0,85f c
Обычно есть две категории решений: когда пластическая нейтральная ось (P.N.A.) проходит через бетонную плиту и через стальное сечение.
Пластическая нейтральная ось проходит через бетонную плиту
Определение положения оси P.N.A. начинается с предположения, что она проходит через бетонную плиту, и попытки рассчитать глубину эквивалентного блока напряжения при сжатии. Если ось P.N.A. находится в пределах плиты, деформация приходится в первую очередь на все стальное сечение, следовательно, сжимающая сила в блоке напряжения в бетоне может быть равна общему растяжению в стали:
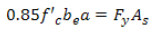
где b e — расчетная ширина бетонной полки, A s — площадь поперечного сечения стальной конструкции, а — глубина блока напряжения при сжатии. Расчет переменной a позволяет определить местоположение оси P.N.A (если a £ t s ) или же понять, что ось P.N.A. проходит через стальное сечение (если a > ts ); недопустимое условие, поскольку для балансировки полного натяжения в стали потребуется больше бетона.
Если ось P.N.A. достоверно проходит через бетонную плиту, номинальный момент нагрузки составного сечения можно найти, добавив момент блока напряжения при сжатии бетона и площадь стали под растяжением. То есть:
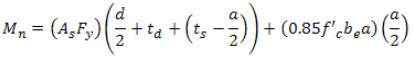
Или еще проще:
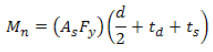
Пластическая нейтральная ось проходит через стальное сечение
Если глубина блока напряжения при сжатии a, необходимого для балансировки полного растяжения стали, превышает толщину перекрытия ts , это указывает на то, что данного объема бетона недостаточно для обеспечения прочности стали на растяжение, а ось P.N.A. проходит через стальное сечение.
Поскольку весь бетон в точке разрушения находится в состоянии сжатия, расположение линии
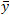оси P.N.A. (как расстояние от низа стального сечения) можно найти, уравновесив суммарные напряжения при сжатии и растяжении:
C c + C s = T s
Геометрия областей напряжения при сжатии и растяжении в стали зависит от места расположения в сечении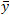 : в верхней полке стальной конструкции, в области сопряжения между верхней полкой и стенкой или в стенке. Но всегда существует уникальное решение для
.
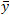Можно проверить, находится ли ось P.N.A. в верхней полке стального сечения. Используйте метод, аналогичный тому, который использовался выше для определения положения оси P.N.A. в бетонной плите. Он заключается в определении прямоугольного блока напряжения при сжатии в стали и балансировке напряжений при сжатии и растяжении. Например, предполагается, что ось P.N.A расположена в нижней части полки. Проверка равновесия усилий на растяжение и сжатие в сечении позволяет определить, где проходит ось P.N.A.: в верхней полке или ниже. Определение положения оси P.N.A. в стенке выполняется аналогично.
Если ось P.N.A. находится в области сопряжения стального сечения, необходимо выполнить аппроксимацию вычисления частичной площади сопряжения. Точное значение площади сопряжения можно найти путем вычитания площади двух полок и стенки из всего поперечного сечения стальной конструкции. Геометрия сопряжения может быть приближена к треугольнику. После определения упрощенной геометрии сопряжения можно рассчитать положение оси P.N.A. в пределах области сопряжения путем расчета частичной площади сопряжения.
Приближение к треугольнику выполняется таким образом, что площадь сопряжения (которая может быть определена размерами сечения в табличной форме) и глубина сопряжения не меняют указанных значений. Ширина сопряжения k w для треугольника определяется на основе этих двух постоянных.
Если
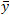находится в пределах сопряжения (т. е. t
f <
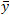< k), площадь стали при сжатии может быть найдена по формуле:
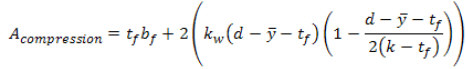
а значит:
A растяжение = A s – A сжатие.
Перестановки и замены позволяют найти уникальное решение для
.
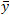После определения общей площади и распределения напряжений можно определить предельный момент путем суммирования результата и длины плеча каждого блока напряжения. Однако определение центра тяжести блоков напряжений в стальном сечении значительно упрощается, если предположить, что вся балка находится в состоянии чистого растяжения или изгиба (для несоставных балок), и добавить блоки растяжения или сжатия для исключения разницы.