关于连续性
连续性是对两个曲线或曲面相互“衔接”的情况的度量。
在“Curves”工具箱中,选择“Blend Curve Toolbox” 。
。
为什么要设置连续性和曲线阶数
- 若要使相交处看起来更加平滑,可以提高连续性级别。
- 若要提高可以实现高级别连续性的灵活度,可以增大曲线阶数。
连续性类型
连续性是两个曲线或曲面之间的过渡的平滑度的数学表示。
下表列出了 Alias 工具可能包含的五种连续性类型:G0 到 G4。注意,G3 和 G4 连续性只适用于过渡曲线。
位置连续性 (G0)
两条曲线的端点必须完全重合。请注意,在任意角度重合的两条曲线仍然具有位置连续性。
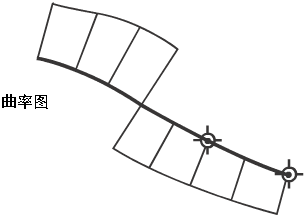

切线连续性 (G1)
在保持位置连续性的同时,在公共端点处的端点切线也要相同。在接合处,两条曲线看起来是沿着相同的方向行进,但却可能有着截然不同的“速度”(改变方向的速率,也称为曲率)。
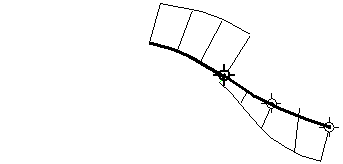
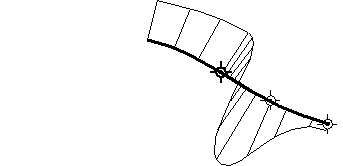
例如,在下图中,两条曲线在接合处(点)有相同的切线(双箭头线)。但是,接合处左侧的曲线在接合处的曲率较慢(低),而接合处右侧的曲线在接合处的曲率较快(高)。

曲率连续性 (G2)
在保持切线连续性的同时,在公共端点处两条曲线的曲率也要相同。两条曲线在接合处似乎具有相同的“速度”。
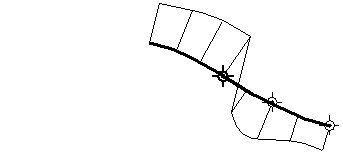
曲率变化率连续性 (G3)。
在保持曲率连续性 (G2) 的同时,曲线之间的曲率变化率也要相同。
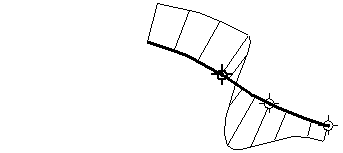
曲率变化率的变化率连续性 (G4)
在保持 G3 连续性的同时,曲线之间曲率变化率的变化率也要相同。这是最平滑的接合类型。
“变化率的变化率”这一概念可能很难概念化。注意下列函数图像:
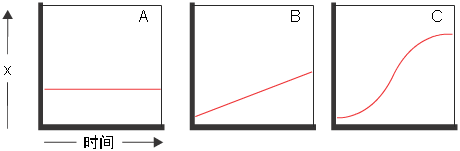
- 在左侧的函数图像 A 中,x 的值不变,所以 x 的变化率是 0。
- 在中间的函数图像 B 中,x 具有恒定的变化率,我们可以据此计算出直线的斜度。
- 在右侧的函数图像 C 中,变化率不是恒定的:最初比较慢,逐渐加快,然后再变慢。变化率本身的变化率就是“变化率的变化率”。