参数是点在曲线或曲面上的唯一数值（类似于坐标）。可以将曲线视为由无数个点组成。形成曲线的每个点具有一个数字，称为点的参数。参数越高，点在曲线上距离起始点越远。

就像空间中的点有三个维（称为 X、Y 和 Z）一样，点的参数沿着曲线的一个内部维（长度）进行测量。我们将此维称为 U。

因为曲面有两个内部维（长度和宽度），所以，我们需要另一个参数（除了 U 之外）才能指定曲面上的点。我们将此参数称为 V。

就像曲线长度方向上的每个点都具有 U 参数一样，曲面上的每个点都具有一对 U 和 V 参数。

什么是参数化？

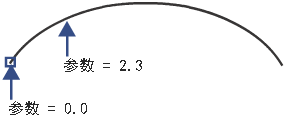
Alias 用于沿曲线计算点数的方法称为曲线的参数化。Alias 有两种参数化方法：统一均分和弦长。

根据曲线的使用方式，这两种方法各有优缺点。可以在创建曲线时选择要使用的参数化方法，也可以重建现有曲线来使用特定的参数化方法。

统一均分参数化

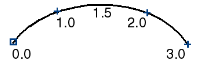
统一均分参数化方法为编辑点指定整数参数值，并使参数在编辑点之间的跨距上均匀分布。所以，第一个编辑点始终是参数 0.0，第二个编辑点始终是 1.0，第三个编辑点始终是 2.0，依此类推。

统一均分参数化有一个可利用的特点：最后一个编辑点的参数值也就是曲线中的跨距数。但是，与弦长参数化方法不同，统一均分曲线的参数不影响曲线的实际长度。

Chord-length Parameterization

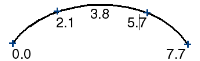
弦长参数化方法为曲线的起点指定参数 0.0，然后根据相邻编辑点之间的弦长（即最短直线距离）按等比增大该参数值。

与统一均分参数化方法不同，弦长曲线的参数在编辑点之间的间距是不均匀的，编辑点没有整数参数。

比较

根据曲线或曲面的使用方式，每种参数化方法各有优缺点。

类型	优点	缺点
弦长	参数值在某种程度上指出了点在曲线上的相对位置。使纹理的拉伸和压缩最小化。	参数不直观。通过弦长曲线构建的曲面由于插入了交叉节点，可能会更加复杂。
统一均分	参数易于估计（例如，1.5 大约是编辑点 1.0 和 2.0 的中点）。	在许多情况下，编辑点之间的插值不是很好，会导致在渲染期间出现无法预测的纹理拉伸。

就像阶数一样，曲面对 U 维和 V 维可以采用不同的参数化方法。例如，曲面的 U 等参线的阶数可以是 3 并采用统一均分参数化方法，而 V 等参线的阶数是 1 并采用弦长参数化方法。