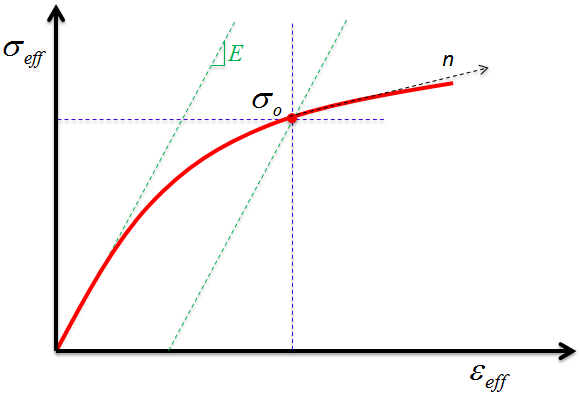
基体成分材料的响应由 Ramberg-Osgood 塑性模型 [13] 提供，该模型已得到增强以允许预测的塑性响应表现出对相对于纤维方向的载荷方向的敏感性。基体成分材料的有效硬化屈服强度可以表示为

其中，σ0 和 n 是标准（各向同性）Ramberg-Osgood 塑性模型所用的典型材料参数，而 εp,eff 则是基体成分材料中的有效塑性应变。当基体成分中的有效应力与硬化屈服强度相匹配时，屈服函数会得到满足。

对于各向同性材料，有效（标量）应力通常是由 von Mises 应力表示。

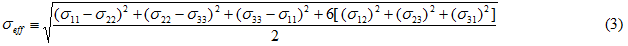
不用说，应力组件表示基体成分材料中的平均应力。类似于有效硬化屈服强度，有效应力也是有效塑性应变 εp,eff 的函数，因为基体成分材料的瞬时切线模量 Etan 要用于计算应力分量，而 Etan 依赖于有效塑性应变 εp,eff，如以下方程中所示。

在方程4 中，H 是基体成分材料的塑性模量，并且以 εp,eff 表示，如下所示。

因此，在施加的总应变增量期间确定塑性演变会降低为查找允许材料状态保留在扩展屈服表面的 εp,eff 值；即我们会反复求解方程 2 以查找 εp,eff。

Ramberg-Osgood 模型（方程 1-5）可以预测各向同性的塑性响应。但是，对于具有高度纤维对齐的短纤维填充塑料，塑性在最终断裂前显示的程度将大大取决于相对于强化纤维的平均方向的载荷方向。Ramberg-Osgood 模型可以轻松增强以适应方向依存关系。为此，我们只需修改有效应力的形式（方程3）。在当前模型中，修改的有效应力表示为

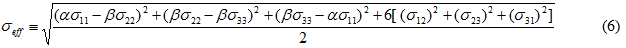
其中 α 和 β 为用于区分与垂直于平均纤维方向的应力组件相比较的平均纤维方向中应力组件的影响。在此与方向相关的公式中，定义材料响应的塑性参数为 σ0、n、α 和 β。

对于拉伸主导的应力状态下的塑性响应增量，我们使用塑性参数的拉伸版本：σ0+、n+、α+ 和 β+。对于压缩主导的应力状态下的塑性响应增量，我们使用塑性参数的压缩版本：σ0-、n-、α- 和 β-*。对于每个规定的应变增量，执行相同的计算，以确定 *εp,eff 的演变，而不管应力状态是拉伸还是压缩。

应该强调的是，当纤维对齐度相对较高时，材料仅显示强方向相关性。当纤维随机定向时，塑性响应必须还原为各向异性响应。若要适应这些特性，方向相关的权重系数 (α、β) 不能是常量。相反，它们必须是纤维对齐度的函数。在当前模型中，假定 α 和 β 是纤维对齐度的线性函数，该函数由纤维取向张量的最大特征值 λI 进行量化。

在方程7 和 8 中，αm 和 βm 分别是 α 和 β 的值，这些值已经过优化以适应具有最大纤维取向特征值 λm,I 的强对齐材料的响应特征。θ 是当纤维方向为随机时，α 和 β 应该实现的值。请注意，λI 的范围从 1.0（适用于完全对齐的材料）到 1/3（适用于在全部三个方向上都使用完全随机的纤维取向的材料，即完全各向同性条件）。

但是，薄的注射成型零件不可能发生真正三维随机分布纤维的条件。更可能的情况是，薄的注射成型零件可能包含一些在注射成型零件的平面中显示随机纤维取向而非零件的厚度方向上的位置（即 λI = 1/2）。为了适应各向同性的更常见形式，方程7 和 8 包含确保当 λI = 1/2 时，α 和 β 各自实现 θ 的相同值的系数 (λI - 1/2)，因此材料成为各向同性材料。