通用计算公式
弹簧外径
D 1 = D + d [in]
其中:
|
D |
弹簧中径 [in] |
|
|
d |
钢丝直径 [in] |
弹簧内径
D 2 = D - d [in]
其中:
|
D |
弹簧中径 [in] |
|
|
d |
钢丝直径 [in] |
预载时的弹簧扭矩
![]()
其中:
|
F 1 |
预承载时弹簧的工作扭矩 [lb] |
|
|
R 1 |
作用力臂 [in] |
满载时的弹簧扭矩
![]()
其中:
|
F 8 |
工作扭矩(弹簧满载时)[lb] |
|
|
R 1 |
作用力臂 [in] |
弹簧指数
i = D/d [-]
其中:
|
D |
弹簧中径 [in] |
|
|
d |
钢丝直径 [in] |
工作行程角
ϕ h = ϕ 8 - ϕ 1 [°]
其中:
|
ϕ 8 |
满载时弹簧的工作臂偏转角 [°] |
|
|
ϕ 1 |
预载时弹簧的工作臂偏转角 [°] |
最小工作臂偏转角
![]()
其中:
|
M 1 |
预承载时弹簧的扭矩 [lb ft] |
|
|
k |
扭簧比 [lb ft/°] |
|
|
ϕ h |
工作行程角 [°] |
|
|
M 8 |
满载时的弹簧扭矩 [lb ft] |
最大工作臂偏转角
![]()
其中:
|
M 1 |
预承载时弹簧的扭矩 [lb ft] |
|
|
k |
扭簧比 [lb ft/°] |
|
|
ϕ h |
工作行程角 [°] |
|
|
M 8 |
满载时的弹簧扭矩 [lb ft] |
应力集中系数
![]()
其中:
|
i |
弹簧指数 [-] |
|
|
i = D/d [-] |
用于计算有效螺旋中的弯曲应力 |
|
|
|
用于计算力臂的弯曲应力 |
|
|
r |
力臂(内部)的弯曲半径 [in] |
|
|
d |
钢丝直径 [in] |
通常情况下弹簧材料的应力
![]()
其中:
|
M |
通常情况下弹簧的扭矩 [Nm] |
|
|
K f |
应力集中系数 [-] |
|
|
d |
钢丝直径 [in] |
弹簧的有效簧圈数
![]()
其中:
| ϕ |
通常情况下的工作臂偏转角 [°] |
|
|
E |
弹性模量 [psi] |
|
|
d |
钢丝直径 [in] |
|
|
M |
通常情况下弹簧的扭矩 [lb ft] |
|
|
R 1 |
作用力臂 [in] |
|
|
R 2 |
支承力臂 [in] |
|
|
D |
弹簧中径 [in] |
弹簧设计计算
在设计弹簧时,钢丝直径、圈数及弯钩臂的弯曲直径的设计都必须符合特定的载荷、材料和装配尺寸。设计的弹簧应符合建议的丝径。对于簧圈之间有间隙的弹簧,自由状态下弹簧螺距之间的节距 t 必须保持在 0.3 D ≤ t ≤ 0.5 D [in] 的范围内。
根据某些弹簧几何尺寸的 (σ 8 ≤ u s sA) 和 (σ 8r ≤ u s σ A ) 强度条件和建议范围进行弹簧设计。
L Z ≤ 10 D 和 L Z ≤ 31.5 in 和 4 ≤ D/d ≤ X 和 n≥ 1.5 和 1.2 d ≤ t < D 和 r ≥ d。
其中:
- 线圈密绕的弹簧 X = 16
- 线圈疏绕的弹簧 X = 10
根据指定的力臂形状和力臂长度,弹簧尺寸应符合可行的几何解决方案。如果按照规范设置,尺寸就一定符合安装尺寸的限制,即许用的最大弹簧外壳直径及长度,或许用的最大杆直径。
指定的最大载荷、材料和弹簧装配尺寸
首先,校核用于计算的输入值并对其进行计算。
然后,根据指定的最大载荷和装配尺寸,来计算最小载荷。
![]()
其中:
|
M 1 |
预承载时弹簧的扭矩 [lb ft] |
|
|
M 8 |
满载时的弹簧扭矩 [lb ft] |
|
|
ϕ 1 |
预载时弹簧的工作臂偏转角 [°] |
|
|
ϕ 8 |
满载时弹簧的工作臂偏转角 [°] |
设计钢丝直径和簧圈数,以便在计算出弹簧直径后,能够满足上述强度和几何条件。如果规范中限定了弹簧的直径值,则弹簧设计必须符合此条件。否则,弹簧直径的限制将由最小和最大许用钢丝直径的几何条件确定。
对于有钩臂的弹簧,需设计出适当的力臂弯曲半径。
按照钢丝直径从小到大的顺序,计算符合指定强度和几何条件的所有弹簧钢丝直径。然后,测试适当的线圈数所需的所有条件是否都符合。如果所有条件都符合,则使用选定的值(不管其是否符合弹簧钢丝直径)完成设计,同时采用最小的可行钢丝直径、最少圈数以及最低弹簧直径来设计弹簧。
指定的载荷、材料和工作变形角
首先,校核用于计算的输入值。
接下来,针对指定的载荷和工作扭转角,计算工作扭矩扭转角。
最小工作臂变形
![]()
最大工作臂变形
![]()
其中:
|
M 1 |
预承载时弹簧的扭矩 [lb ft] |
|
|
M 8 |
满载时的弹簧扭矩 [lb ft] |
|
|
ϕ 1 |
预载时弹簧的工作臂偏转角 [°] |
|
|
ϕ 8 |
满载时弹簧的工作臂偏转角 [°] |
|
|
ϕ h |
工作行程角 [°] |
然后,设计钢丝直径和簧圈数,以便在计算出弹簧直径后,能够满足上述强度和几何条件。如果规范中限定了弹簧的直径值,则弹簧设计必须符合此条件。否则,弹簧直径的限制将由最小和最大许用钢丝直径的几何条件确定。
对于有钩臂的弹簧,需设计出适当的力臂弯曲半径。
按照钢丝直径从小到大的顺序,考虑符合指定强度和几何条件的所有弹簧钢丝直径。然后,测试适当的圈数所需的条件是否符合。如果所有条件都符合,则使用选定的值(不管其是否符合弹簧钢丝直径)完成设计,同时采用最小的可行钢丝直径、最少圈数以及最低弹簧直径来设计弹簧。
指定的最大载荷、材料和弹簧直径
首先,校核用于计算的输入值。
然后,设计钢丝直径、簧圈数和装配尺寸,以满足上述强度和几何条件。如果规范中限定了工作扭转角的值,则弹簧设计必须符合此条件。否则,装配尺寸的限制将由指定的弹簧直径和最小或最大许用钢丝直径的几何条件确定。
对于有钩臂的弹簧,需计算出适当的力臂弯曲半径。
考虑所有具有指定强度和几何条件的弹簧钢丝直径,并按钢丝直径从小到大的递增顺序计算出相应的设计。然后,测试圈数所需的所有条件是否都符合。如果所有条件都符合,则使用选定的值(不管其是否符合弹簧钢丝直径)完成设计,同时采用最小的可行钢丝直径、最少圈数以及最低弹簧直径来设计弹簧。
指定的最大载荷、材料、弹簧直径和工作变形角
首先,校核用于计算的输入值。
然后,优化钢丝直径、簧圈数和工作臂的偏转角,以满足上述强度和几何条件。该程序寻求最大工作臂偏转角中的最小值 ϕ 8 ,其中会考虑最小工作臂偏转角 ϕ 1 约等于 2°的要求。
对于有钩臂的弹簧,需计算出适当的力臂弯曲半径。
最后,针对指定的最大载荷和设计出的工作扭矩扭转角,计算最小弹簧载荷。
![]()
其中:
|
M 1 |
预承载时弹簧的扭矩 [lb ft] |
|
|
M 8 |
满载时的弹簧扭矩 [lb ft] |
|
|
ϕ 1 |
预载时弹簧的工作臂偏转角 [°] |
|
|
ϕ 8 |
满载时弹簧的工作臂偏转角 [°] |
弹簧校验计算
针对指定的载荷、材料和弹簧尺寸,计算对应的装配尺寸值。首先,校核并计算输入数据,然后使用以下公式计算装配尺寸。
最小工作臂偏转角
![]()
其中:
|
M 1 |
预承载时弹簧的扭矩 [lb ft] |
|
|
D |
弹簧中径 [in] |
|
|
n |
有效簧圈数 [-] |
|
|
R 1 |
作用力臂 [in] |
|
|
R 2 |
支承力臂 [in] |
|
|
E |
弹性模量 [psi] |
|
|
d |
钢丝直径 [in] |
最大工作臂偏转角
![]()
其中:
|
M 1 |
预承载时弹簧的扭矩 [lb ft] |
|
|
D |
弹簧中径 [in] |
|
|
n |
有效簧圈数 [-] |
|
|
R 1 |
作用力臂 [in] |
|
|
R 2 |
支承力臂 [in] |
|
|
E |
弹性模量 [psi] |
|
|
d |
钢丝直径 [in] |
工作行程角
ϕ h = ϕ 8 - ϕ 1 [°]
其中:
|
M 8 |
满载时的弹簧扭矩 [lb ft] |
|
|
ϕ 8 |
满载时弹簧的工作臂偏转角 [°] |
作用力计算
针对指定的材料、装配尺寸和弹簧尺寸,计算处于其工作状态下的弹簧产生的相应载荷。校核和计算输入数据,然后使用以下公式计算工作扭矩。
最小工作载荷
![]()
![]()
其中:
|
M 1 |
预承载时弹簧的扭矩 [lb ft] |
|
|
ϕ 1 |
预载时弹簧的工作臂偏转角 [°] |
|
|
D |
弹簧中径 [in] |
|
|
n |
有效簧圈数 [-] |
|
|
R 1 |
作用力臂 [in] |
|
|
R 2 |
支承力臂 [in] |
|
|
E |
弹性模量 [psi] |
|
|
d |
钢丝直径 [in] |
最大工作载荷
![]()
![]()
其中:
|
M 8 |
满载时弹簧的扭矩 [Nm] |
|
|
ϕ 8 |
满载时弹簧的工作臂偏转角 [°] |
|
|
D |
弹簧中径 [in] |
|
|
n |
有效簧圈数 [-] |
|
|
R 1 |
作用力臂 [in] |
|
|
R 2 |
支承力臂 [in] |
|
|
E |
弹性模量 [psi] |
|
|
d |
钢丝直径 [in] |
弹簧输出参数计算
可用于所有类型的弹簧计算,计算时按照以下顺序进行。
扭簧比
![]()
自由弹簧簧圈之间的间距
a = t - d [mm]
自由弹簧螺旋部分的长度
|
对于紧密缠绕的弹簧 |
|
|
L 0 = (1.05 n + 1) d [in] |
|
|
对于松散缠绕的弹簧 |
|
|
L 0 = t n + d [in] |
|
最小工作载荷下有效簧圈中弹簧材料的弯曲应力
![]()
其中,应力集中系数 K f 在 i = D/d 时进行计算
最小工作载荷下力臂弯曲处弹簧材料的弯曲应力
![]()
其中,应力集中系数 K f 在 i = 2r/d + 1 时进行计算
满载状态下有效簧圈中弹簧材料的弯曲应力
![]()
其中,应力集中系数 K f 在 i = D/d 时进行计算
满载状态下力臂弯曲处弹簧材料的弯曲应力
![]()
其中,应力集中系数 K f 在 i = 2r/d + 1 时进行计算
紧密缠绕的弹簧在满载状态下弹簧螺旋部分的长度与载荷盘绕弹簧
![]()
满载状态下的弹簧外径与载荷盘绕弹簧

满载状态下的弹簧内径与载荷盘绕弹簧
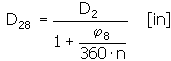
工作臂的极限测试角偏差
![]()
弹簧变形能
![]()
钢丝长度
|
l = 3.2 D n + l R [in] |
||||
|
其中,l R 为臂长,而: |
||||
|
其中,l R 为臂长,而: |
||||
|
直扭臂的长度 |
||||
|
|
||||
|
钩臂长度 |
||||
|
|
||||
弹簧质量
![]()
弹簧载荷的校核
(σ 8 ≤ u s σ A ) 和 (σ 8r ≤ u s σ A )
所用变量的含义:
|
a |
自由状态下有效螺旋的间距 [in] |
|
d |
钢丝直径 [in] |
|
D |
弹簧中径 [in] |
|
D 1 |
弹簧外径 [in] |
|
D 2 |
弹簧内径 [in] |
|
E |
弹性模量 [psi] |
|
F |
弹簧承受的作用力(通常情况下,是作用力的 R 1 臂上承受的力 [lb] |
|
i |
弹簧指数 [-] |
|
K F |
应力集中系数 [-] |
|
kϕ |
扭簧比 [lb ft/°] |
|
r 1 |
工作扭矩的弯曲半径 [in] |
|
r 2 |
支承力臂的弯曲半径 [in] |
|
R 1 |
作用力臂 [in] |
|
R 2 1 |
支承力臂 [in] |
|
l |
弹簧展开长度 [in] |
|
L 0 |
通常情况下处于松弛状态的自由长度 [in] |
|
m |
弹簧质量 [lb] |
|
M |
通常情况下弹簧的扭矩 [lb ft] |
|
n |
有效簧圈数 [-] |
|
t |
松弛状态下螺旋的节距 [in] |
|
u s |
|
| ρ |
弹簧材料的密度 [lb/ft3] |
| ϕ |
通常情况下的工作臂偏转角 [°] |
| σ |
通常情况下弹簧材料的弯曲应力 [psi] |
|
σ A |
弹簧材料的许用弯曲应力 [psi] |
|
M 1 |
预承载时弹簧的扭矩 [lb ft] |
|
M 8 |
满载时的弹簧扭矩 [lb ft] |
|
ϕ 8 |
满载时弹簧的工作臂偏转角 [°] |
|
ϕ 1 |
预载时弹簧的工作臂偏转角 [°] |
|
ϕ 8 |
满载时弹簧的工作臂偏转角 [°] |
|
ϕ h |
满载时弹簧的工作臂偏转角 [°] |