检查压缩弹簧的疲劳载荷

对于承受动态载荷的弹簧（即，承受循环载荷变化并且要求的寿命大于 10 ⁵ 个工作行程的弹簧），根据 τ ₈ ≤ u _s τ _A 公式进行的常规静态应力检查是不够的。必须对此类弹簧进行弹簧材料的疲劳载荷校核。

如果要使此类弹簧满足预期动态载荷，则除了上述的静态检查外，τ ₈ ≤τ _e /k _f 公式中的条件还必须为真。可以根据特定的钢丝直径、材料、寿命要求和弹簧载荷在相应的“史密斯疲劳曲线”中获得 te 疲劳极限。

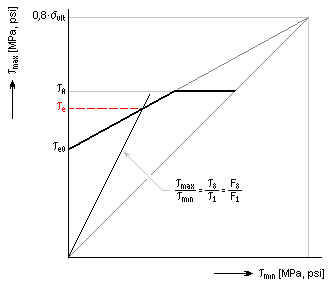
其中：

F 1	最小工作扭矩 [N, lb]
F 8	最大工作扭矩 [N, lb]
k f	疲劳极限时的安全系数 [-]
N	弹簧大量变形量时的寿命 [-]
σ ult	弹簧材料的极限拉伸应力 [MPa, psi]
τ 1	预承载时弹簧材料的扭应力 [MPa, psi]
τ 8	完全承载时弹簧材料的扭应力 [MPa, psi]
τ e	承受疲劳载荷弹簧的剪切疲劳极限 [MPa, psi]
τ e0	零平均应力剪切时的基本疲劳极限 [MPa, psi]
τ A	弹簧材料许用扭应力 [MPa, psi]

零平均应力时的材料基本疲劳极限 τ _e0 的数据显示在试验数据图（参见下图）中。这些数据的有效性由特定材料、表面光洁度和弹簧寿命确定。

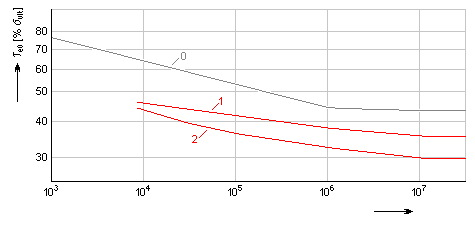
其中：

	曲线 0	用于符合所需寿命的钢弹簧的基本疲劳极限 te0 的理论计算曲线
	曲线 1	用于喷丸强化处理的基本疲劳极限的最大建议值
	曲线 8	用于未喷丸强化处理的基本疲劳极限的最大建议值