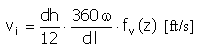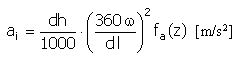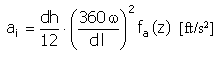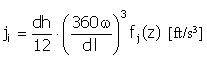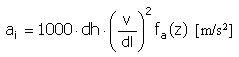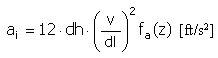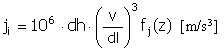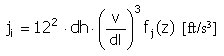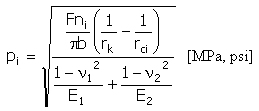凸輪計算方程式

輸入資料：

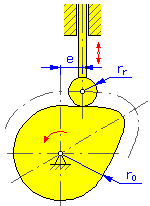
• 基準半徑 r ₀ (圓盤和圓柱凸輪)
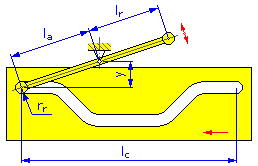
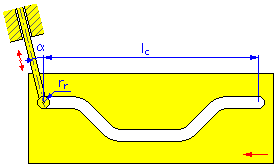
• 運動長度 l _c (線性凸輪)
• 凸輪寬度 b _c
• 滾子半徑 r _r
• 滾子寬度 b _r (用於從動輪造型圓柱)
• 離心率 e (用於轉換從動輪的圓盤凸輪)
• 離心角 α (用於轉換從動輪的線性和圓柱凸輪)
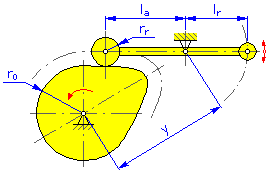
• 軸心距離 y (用於擺動臂的圓盤和線性凸輪)
• 臂長 l _a (用於擺動臂的圓盤和線性凸輪)
• 反作用力臂 l _r (用於擺動臂的圓盤和線性凸輪)
• 速度 ω (圓盤和圓柱凸輪)
• 速度 v (線性凸輪)
• 滾子上的力 F
• 加速權值 m
• 彈簧額定值 c
• 允許的壓力 p _A1
• 凸輪材料的彈性係數 E ₁
• 凸輪材料的蒲松氏比 μ ₁
• 允許的壓力 p _A2
• 從動輪材料的彈性係數 E ₂
• 從動輪材料的蒲松氏比 μ ₂

圓盤形凸輪
線性凸輪
圓柱凸輪
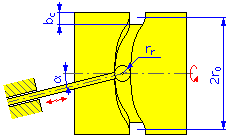外徑 = 2r 0 + b c
內徑 = 2r 0 - b c

凸輪段

• 運動功能 f _y (z) [ul]
• 反轉比率 k _r (僅用於線性部分的拋物線運動)
• 線性部分 k _l (僅用於線性部分的拋物線運動)
• 運動起始位置 l ₀ [°; mm, in]
• 運動終止位置 l [°; mm, in]
• 段運動長度 dl = l - l ₀ [°; mm, in]
• 起始位置升程 h ₀ [mm, in]
• 末端升程 h _max [mm, in]
• 段升程 d _h = h _max - h ₀ [mm, in]

升程相依性

圓盤和圓柱凸輪

凸輪旋轉角度 ϕ _i [°]

在段中的實際相對位置：z _i = (ϕ _i - l ₀ ) / dl (range 0 - 1)

升程	y i = dh f y (z) [mm, in]
速度
加速度
脈衝

線性凸輪

凸輪運動位置 l _i [mm, in]

在段中的實際相對位置：z _i = (l _i - l ₀ ) / dl (範圍 0～1)

升程	y i = dh f y (z) [mm, in]
速度
加速度
脈衝

運動功能

擺線 (延伸的正弦曲線)

此運動具有極好的加速度特性。由於其可產生低噪音、低震動和低磨損的結果，因此常用於高速凸輪。

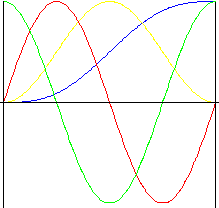
	升程
	速度
	加速度
	脈衝

升程	f y (z) = z - 0.5/π sin(2πz)
速度	f v (z) = 1 - cos (2πz)
加速度	f a (z) = 2π sin(2πz)
脈衝	f j (z) = 4π 2 cos(2πz)

調和 (正弦)

行程期間速度和加速度的平穩性是此曲線的固有優點。但是，在運動起始和終止時的瞬時變更容易產生震動、噪音和磨損。

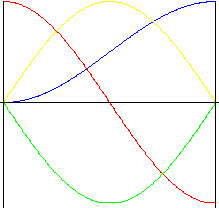
	升程
	速度
	加速度
	脈衝

升程	f y (z) = 0.5 (1 - cos πz))
速度	f v (z) = 0.5 π sin (πz)
加速度	f a (z) = 0.5 π 2 cos(πz)
脈衝	f j (z) = -0.5π 3 sin(πz)

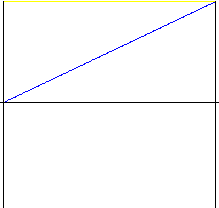
線性

在運動起始和終止時會產生巨大衝擊的簡單運動。除非常簡單的裝置以外，很少使用。建議使用已對運動起始和終止時狀態進行過修改的運動 – 具有線性部分的拋物線。

	升程
	速度

升程	f y (z) = z
速度	f v (z) = 1
加速度	f a (z) = 0
	註: z = 0 和 z = 1 時，正確的值應該是無限值，但計算時不能使用無限值，因此要使用零值。
脈衝	f j (z) = 0
	註: z = 0 和 z = 1 時，正確的值應該是無限值，但計算時不能使用無限值，因此要使用零值。

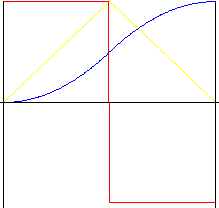
拋物線 (2 階 多項式)

具有最小可能加速度的運動。但是，由於在運動起始和終止以及中期中加速度會突然發生變更，因此會產生衝擊。反轉比率允許運動中期「拉伸」，以允許加速度和減速度比率發生變更。

對稱 (反轉比率 k _r = 0.5)

	升程
	速度
	加速度

	z = 0 到 0.5 之間時：
		升程	fy(z) = 2z 2
		速度	fv(z) = 4z
		加速度	fa (z) = 4
		脈衝	fa(z) = 0
	z = 0.5 - 1 時：
		升程	fy(z) = 1 - 2(1 - z) 2
		速度	fv(z) = 4 (1 - z)
		加速度	fa (z) = -4
		脈衝	fj(z) = 0
			註: z = 0 和 z = 1 時，正確的值應該是無限值，但計算時不能使用無限值，因此要使用零值。

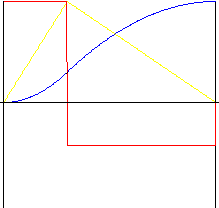
非對稱

k _r - 反轉比率 (範圍在 0.01 到 0.99 之間)

	升程
	速度
	加速度

	z = 0 到 k r 之間時：
		升程	f y (z) = z 2 / k r
		速度	f v (z) = 2z / k r
		加速度	f a (z) = 2 / k r
		脈衝	f j (z) = 0
	z = k r 到 1 之間時：
		升程	f y (z) = 1 – (1 – z) 2 / (1 – k r )
		速度	f v (z) = 2 (1 – z) / (1 – k r )
		加速度	f a (z) = -2 / (1 - k r )
		脈衝	f j (z) = 0
			註: z = 0 和 z = 1 時，正確的值應該是無限值，但計算時不能使用無限值，因此要使用零值。

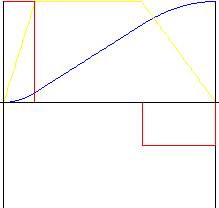
具有線性部分的拋物線

與線性運動相比，可提供更令人滿意的加速度和減速度。反轉比率允許運動中期「拉伸」，以允許加速度和減速度比率發生變更。線性部分比率允許設定線性運動部分的相對大小。

	速度
	加速度
	脈衝

k _r - 反轉比率 (範圍在 0.01 到 0.99 之間)

k _l - 線性部分比率 (範圍在 0 到 0.99 之間)

k _z = 1 + k _l / (1 - k _l )

k _h = (1 - k _l ) / (1 + k _l )

	z = 0 到 k r / k z 之間時：
		升程	f y (z) = k h z 2 k z 2 / k r
		速度	f v (z) = 2 k h z k z 2 / k r
		加速度	f a (z) = 2 k h k z 2 / k r
		脈衝	f j (z) = 0
	z = k r / k z 到 r / k z + k l 之間時：
		升程	f y (z) = (z - 0.5 k r / k z ) 2 / (1 + k l )
		速度	f v (z) = 2 / (1 + k l )
		加速度	f a (z) = 0
		脈衝	f j (z) = 0
	z = k r / k z + k l 到 1 之間時：
		升程	f y (z) = 1 - k h (1 - z) 2 k z 2 / (1 - k r )
		速度	f v (z) = 2 k h (1 - z) k z 2 / (1 - k r )
		加速度	f a (z) = -2 k h k z 2 / (1 - k r )
		脈衝	f j (z) = 0

3 階 多項式 (立方拋物線)

比拋物線運動產生更小衝擊的運動。

	升程
	速度
	加速度
	脈衝

升程	f y (z) = (3 -2z) z 2
速度	f v (z) = (6 - 6z) z
加速度	f a (z) = 6 - 12z
脈衝	f j (z) = -12

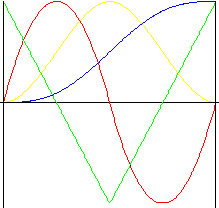
4 階 多項式

比 3 階多項式運動產生更小衝擊的運動。

	升程
	速度
	加速度
	脈衝

z = 0 - 0.5 時
	升程	f y (z) = (1 - z) 8z 3
	速度	f v (z) = (24 - 32z) z 2
	加速度	f a (z) = (48 - 96z) z
	脈衝	f j (z) = 48 - 192z
z = 0.5 到 1 之間時，
	升程	f y (z) = 1 - 8z (1 - z) 3
	速度	f v (z) = (32z - 8) (1 - z) 2
	加速度	f a (z) = (48 - 96z) (1 - z)
	脈衝	f j (z) = 194z - 144

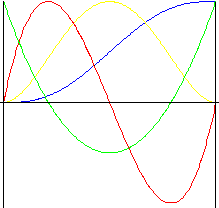
5 階 多項式

比 3 階多項式運動產生更小衝擊的運動。

	升程
	速度
	加速度
	脈衝

升程	f y (z) = (6z 2 - 15z + 10) z 3
速度	f v (z) = (z 2 - 2z + 1) 30z 2
加速度	f a (z) = (2z 2 - 3z + 1) 60z
脈衝	f j (z) = (6z 2 - 6z + 1) 60

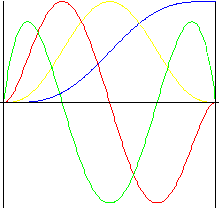
7 階 多項式

在所有公式 (包括脈衝) 中的平穩性。

	升程
	速度
	加速度
	脈衝

升程	f y (z) = (-20z 3 + 70z 2 - 84z + 35) z 4
速度	f v (z) = (-z 3 + 3z 2 - 3z + 1) 140z 3
加速度	f a (z) = (-2z 3 + 5z 2 - 4z + 1) 420z 2
脈衝	f j (z) = (-5z 3 + 10z 2 - 6z + 1) 840z

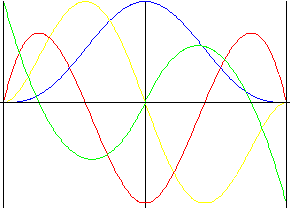
非對稱 5 階 多項式

與 5 階多項式類似，但是具有強迫式升程反轉。

註: 需要結合第 1 部分和第 2 部分。

	升程
	速度
	加速度
	脈衝

第 1 部分
	升程	f y (z) = 1 - (8 (1 - z) 3 - 15 (1 - z) 2 + 10) (1 - z) 2 / 3
	速度	f v (z) = (2 (1 - z) 3 - 3 (1 - z) 2 + 1) (1 - z) 20 / 3
	加速度	f a (z) = -(8 (1 - z) 3 - 9 (1 - z) 2 + 1) 20 / 3
	脈衝	f j (z) = (4 (1 - z) 2 - 3 (1 - z)) 40

第 2 部分
	升程	f y (z) = (8z 3 - 15z 2 + 10) z 2 / 3
	速度	f v (z) = (2z 3 - 3z 2 + 1) z 20/3
	加速度	f a (z) = (8z 3 - 9z 2 + 1) 20/3
	脈衝	f j (z) = (4z 2 - 3z) 40

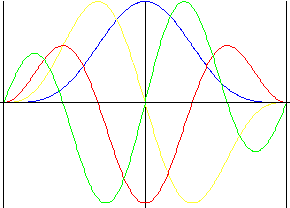
雙調和

在所有公式 (包括具有強迫式升程反轉的脈衝) 中的平穩性。

註: 需要結合第 1 部分和第 2 部分。

第 1 部分
	升程	f y (z) = cos(0.5π (1 - z)) 4
	速度	f v (z) = π (0.5 sin(πz) - 0.25 sin(2πz))
	加速度	f a (z) = 0.5 π 2 (cos(πz) - cos(2πz))
	脈衝	f j (z) = π 3 (-0.5 sin(πz) + sin(2πz))

第 2 部分
	升程	f y (z) = 1 - cos(0.5π z) 4
	速度	f v (z) = π (0.5 sin(πz) + 0.25 sin(2πz))
	加速度	f a (z) = 0.5 π 2 (cos(πz) + cos(2πz))
	脈衝	f j (z) = -π 3 (0.5 sin(πz) + sin(2πz))

最大相對值的比較

運動	速度	加速度	脈衝
擺線 (延長正弦曲線)	2	6.28	39.5
諧波 (正弦)	1.57	4.93	15.5
「線性」	1	∞	∞
拋物線 (2 階多項式)	2	4	∞
3 階多項式	1.5	6	12
4 階多項式	2	6	48
5 階多項式	1.88	5.77	60
7 階多項式	2.19	7.51	52.5
非對稱 5 階多項式	1.73	6.67	40
雙諧	2.04	9.87	42.4

其他相依性

作用於滾子上的力

F i = F + m a i + c y i [N, lb]

正垂力

Fn i = F i / cos (γ i ) [N, lb]

力矩

T i = F i r i tan (γ i ) [Nmm, lb in]

特定 (赫茲) 壓力

	b = min (b v, b k )