Mathematische Konzepte
Die folgenden Abschnitte enthalten Definitionen von einigen der mathematischen Terme, die mit der Lösung von CFD-Gleichungen in Verbindung stehen.
Linear - Nicht linear
Die zugrunde liegenden Gleichungen finden Sie im nächsten Abschnitt. Diese Gleichungen können zwei Arten von Nicht-Linearitäten enthalten. Der erste Typ Nicht-Linearität wird durch die Advektionsterme veranschaulicht. Beispiel: In der Gleichung zur Geschwindigkeit u wird ein Term angezeigt:
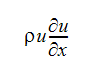
In den folgenden Termen hängt also u vom Produkt aus u und seiner Ableitung ab. Die zweite Art Nicht-Linearität, die in der zugrunde liegenden Gleichung auftritt, ist, dass die Eigenschaften oder Faktoren der Terme von der abhängigen Variablen abhängen. Die Dichte in der Energiegleichung hängt beispielsweise von der Temperatur ab, für die die Gleichung gelöst wird. Die Wirbelviskosität für turbulente Strömungen für die Diffusionsterme in den Geschwindigkeitsgleichungen ist auch in hohem Maße abhängig von den Geschwindigkeiten. Diese beiden Typen von Nicht-Linearitäten stellen bei weitem die vorherrschenden Einflüsse auf die numerische Lösung dar. Aus diesem Grund müssen die Gleichungen auf iterative Weise gelöst werden.
Explizit - Implizit
Wenn ein Term implizit behandelt wird, wird er Teil der Koeffizientenmatrix und damit Teil der Lösung. Wenn er explizit behandelt wird, werden Werte aus vorherigen Iterationen anstelle der aktuellsten Informationen verwendet. Diese Terme sind gewöhnlich Teil des Quellterms oder des Lastvektors. Sie werden nach der Lösung der aktuellen Iteration festgelegt. Für die numerische Stabilität ist es am besten, so viele Terme wie möglich implizit zu behandeln.
Für transiente Analysen wird eine implizite Diskretisierungsmethode verwendet. Dies schließt ein, dass der Wert zur aktuellen Zeit von den benachbarten Werten zur aktuellen Zeit abhängt. Eine explizite Diskretisierungsmethode setzt voraus, dass der Wert zur aktuellen von den benachbarten Werten aus der vorherigen Zeit abhängt. Eine implizite Formulierung ist numerisch uneingeschränkt stabil. Sie liefert ungeachtet der Größe des Zeitschritts eine Lösung. Es ist jedoch eine iterative Lösung in jedem Zeitschritt erforderlich. Eine explizite Formulierung ist nur numerisch bedingt stabil. Sie ist sehr stark abhängig und häufig in hohem Maße restriktiv, was die Zeitschrittgröße angeht. Nicht selten werden Zeitschritte von 1.E-10 Sekunden für explizite Formulierungen verwendet. Sie müssen jedoch nicht die Lösung in jedem Zeitschritt wiederholen.
Symmetrisch - Nicht symmetrisch
Die zugrunde liegenden partiellen Differenzialgleichungen im nächsten Abschnitt sind unter Verwendung von finiten Elementen in einen Satz algebraischer Gleichungen diskretisiert, wobei die Unbekannten Knotenwerte der Lösungsvariablen sind. Diese algebraischen Gleichungen können auf folgende Weise in Matrix-Form geschrieben werden:
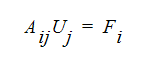
wobei F*i* der Lastvektor, *Uj* der unbekannte Vektor und *Aij*** die Koeffizientenmatrix ist. Für ein symmetrisches System aus Gleichungen sind die oberen Diagonalen von A ein Spiegelbild der unteren Diagonalen, d. h.
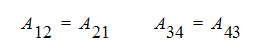
Bei nicht symmetrischen Systemen ist dies nicht der Fall. Im Allgemeinen erzeugen Ableitungsterme zweiter Ordnung (z. B. Diffusionsparameter) symmetrische Matrizen und Ableitungen erster Ordnung (Advektionsparameter) nicht symmetrische Matrizen.