After the completing the Least Squares adjustment, the covariance matrix is used to calculate the positional standard deviations ![]() and
and ![]() .
.
The following illustration shows that standard deviations represent half-dimensions of the standard 68% probability error rectangle around each point:
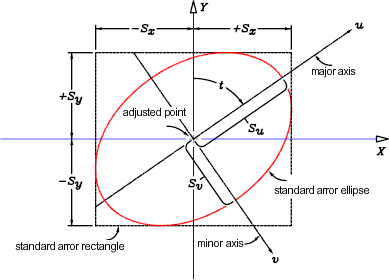
Where:
- t = the orientation of the error ellipse, the direction of the semi-major axis
- u = semi-major axis of the error ellipse
- v = the semi-minor axis error ellipse
- x = half-width dimension of the error rectangle
- y = half-height dimension of the error rectangle
- S = Positional standard deviation of a point