For dynamically loaded springs, that is, springs exposed to cyclic load changes and with the required life of more than 10 5 working strokes, the general static stress check according to the τ 8 ≤ u s τ A formula is not enough. Such spring must be checked for fatigue load of the spring material.
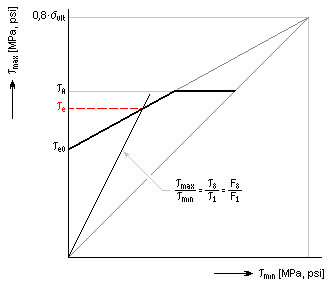
If such spring with expected dynamic load is to be satisfactory, the condition in the τ 8 ≤τ e /k f formula must be true in addition to the previously mentioned static check. The endurance te limit can be found in the respective "Smith's fatigue graph" according to the specific wire diameter, material, life requirements, and spring load.
where:
|
F 1 |
minimum working force [N, lb] |
|
F 8 |
maximum working force [N, lb] |
|
k f |
safety factor at the fatigue limit [-] |
|
N |
spring life in thousands of deflections [-] |
|
σ ult |
ultimate tensile stress of spring material [MPa, psi] |
|
τ 1 |
torsional stress of spring material in the preloaded state [MPa, psi] |
|
τ 8 |
torsional stress of spring material in the fully loaded state [MPa, psi] |
|
τ e |
endurance limit in shear of fatigue loaded spring [MPa, psi] |
|
τ e0 |
basic endurance limit in shear for zero mean stress [MPa, psi] |
|
τ A |
allowable torsion stress of spring material [MPa, psi] |
Data on basic endurance limit of materials for zero mean stress τ e0 are displayed in the experimental data diagram (see the following picture). Validity of these data is given by the specific material, surface finish, and spring life.

where:
|
curve 0 |
theoretically calculated curve of basic endurance limit te0 for steel springs with respect to required life |
|
|
curve 1 |
maximum recommended values of basic endurance limit for shot-peened springs |
|
|
curve 8 |
maximum recommended values of basic endurance limit for non shot-peened springs |