Roller chain can vibrate noticeably when the frequency of an exciting source is close to one of the natural frequencies of the chain. Under certain conditions, the vibration may be so severe that it can damage or destroy the chain or the drive. The major sources of excitement are large cyclic loads, chordal action, and roller-tooth impact.
The natural chain frequencies are computed and transformed to the driver sprocket speeds for better understanding. These speeds are named as critical speeds. If the driver sprocket speed is close to one of the critical speeds the vibrations may occur. The critical interval of driver sprocket speed is determined as follows:
![]()
where:
|
n C |
Critical speed of driver sprocket [rpm] |
|
|
n |
Actual speed of driver sprocket [rpm] |
|
|
Δ n |
Limit of critical speed [-] |
Lateral vibration
In lateral vibration, the chain vibrates up and down (in a horizontal drive) about the chain's axis like a plucked string. It is the most visible, and may be the most common, type of vibration. The natural frequency for lateral vibration is low. The excitation from polygonal effect and large cyclic load may be enough to cause damaging vibration at resonance. The lateral vibration is computed for every span in the chain drive and compared with the current driver sprocket speed.
The critical driver sprocket speed for lateral vibration at each span of the chain drive is given by following equation:
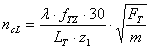
where:
|
n cL |
Critical driver sprocket speed from natural frequency of lateral vibration [rpm] |
|
| λ |
An integer represent the harmonic of the vibration [-] |
|
|
L T |
Length of the chain span [m] |
|
|
F T |
Tension in the chain span [N] |
|
|
f TZ |
Teeth factor [-] (f TZ = 1.2 for z 1 < 18 otherwise f TZ = 1.1) |
|
|
z 1 |
Number of driver sprocket teeth [-] |
|
|
m |
Specific chain mass [kg/m] |
Wave-type vibration
In wave-type vibration, the chain vibrates axially like an elastic bar that is excited at its ends. Wave-type vibration usually cannot be seen. Wave vibration can increase chain tension quite a lot and cause early chain failure. Damaging wave-type vibration can also occur when the tooth contact frequency matches the second harmonic of the natural frequency of the chain.
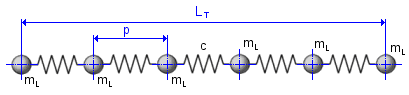
The critical driver sprocket speed for wave-type vibration at each span of the chain drive is given by following equation:
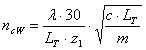
where:
|
n cW |
Critical driver sprocket speed from natural frequency of wave-type vibration [rpm] |
|
| λ |
An integer represent the harmonic of the vibration [-] |
|
|
L T |
Length of the chain span [m] |
|
|
z 1 |
Number of driver sprocket teeth [-] |
|
|
c |
Chain stiffness [N/m] |
|
|
m |
Specific chain mass [kg/m] |
|
Axial, or spring-type, vibration
In the axial vibration, the chain acts like a spring connected between to rotors. This type of vibration is not readily seen, but at resonance it may be identified by increased noise. The impulse from a large cyclic load may be enough to cause damaging vibration at resonance.
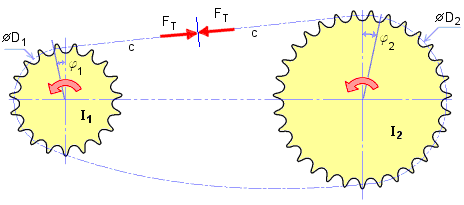
Critical driver sprocket speed from polygonal effect
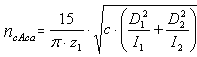
Critical driver sprocket speed from circumferential run-out
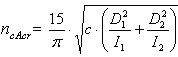
Critical driver sprocket speed from inaccuracy of chain link pitches
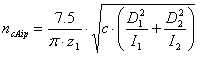
where:
|
n cAca |
Critical driver sprocket speed from polygonal effect [rpm] |
|
|
n cAcr |
Critical driver sprocket speed from circumferential run-out [rpm] |
|
|
n cAip |
Critical driver sprocket speed from inaccuracy of chain link pitches [rpm] |
|
|
z 1 |
Number of driver sprocket teeth [-] |
|
|
c |
Chain stiffness [N/m] |
|
|
D 1 |
Pitch diameter of input sprocket [-] |
|
|
D 2 |
Pitch diameter of output sprocket [-] |
|
|
I 1 |
Rotating moment of inertia related to the input sprocket [kg m 2 ] |
|
|
I 2 |
Rotating moment of inertia related to the input sprocket [kg m 2 ] |