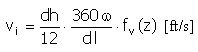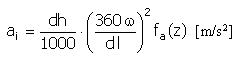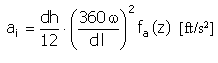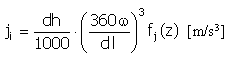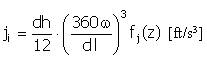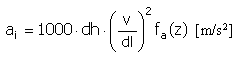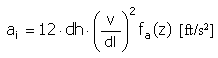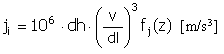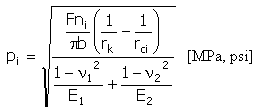Cam Calculation Equations

Input data:

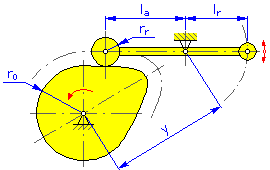
• Basic Radius r ₀ (Disc and Cylindrical Cams)
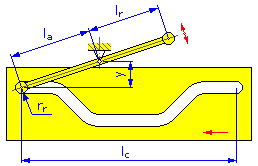
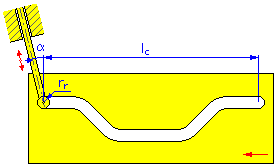
• Motion Length l _c (Linear Cams)
• Cam Width b _c
• Roller Radius r _r
• Roller Width b _r (for Follower Shape Cylinder)
• Eccentricity e (Disc Cams for Translating Follower)
• Eccentricity angle α (Linear and Cylindrical Cams for Translating Follower)
• Pivot Distance y (Disc and Linear Cams for Swinging Arm)
• Arm Length l _a (Disc and Linear Cams for Swinging Arm)
• Reaction Arm l _r (Disc and Linear Cams for Swinging Arm)
• Speed ω (Disc and Cylindrical Cams)
• Velocity v (Linear Cams)
• Force on Roller F
• Accelerated Weight m
• Spring Rating c
• Allowable Pressure p _A1
• Modulus of Elasticity of Cam Material E ₁
• Poisson's Ratio of Cam Material μ ₁
• Allowable Pressure p _A2
• Modulus of Elasticity of Follower Material E ₂
• Poisson's Ratio of Follower Material μ ₂

Disc Cam
Linear Cam
Cylindrical Cam
Outside diameter = 2r 0 + b c
Inside diameter = 2r 0 - b c

Cam Segments

• Motion Function f _y (z) [ul]
• Reverse Ratio k _r (only for motion Parabolic and Parabolic with linear part)
• Linear Part k _l (only for motion Parabolic with linear part)
• Motion Start Position l ₀ [°; mm, in]
• Motion End Position l [°; mm, in]
• Segment Motion Length dl = l - l ₀ [°; mm, in]
• Lift at Start h ₀ [mm, in]
• Lift at End h _max [mm, in]
• Segment Lift d _h = h _max - h ₀ [mm, in]

Lift dependencies

Disc and Cylindrical Cam

Cam rotation angle ϕ _i [°]

Actual relative position in segment: z _i = (ϕ _i - l ₀ ) / dl (range 0 - 1)

Lift	y i = dh f y (z) [mm, in]
Speed
Acceleration
Pulse

Linear Cam

Cam motion position l _i [mm, in]

Actual relative position in segment: z _i = (l _i - l ₀ ) / dl (range 0 - 1)

Lift	y i = dh f y (z) [mm, in]
Speed
Acceleration
Pulse

Motion functions

Cycloidal (extended sinusoidal)

This motion has excellent acceleration characteristics. It is used often for high-speed cams because it results in low levels of noise, vibration, and wear.

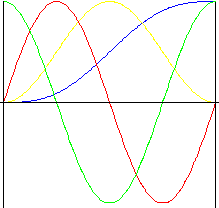
	Lift
	Speed
	Acceleration
	Pulse

Lift	f y (z) = z - 0.5/π sin(2πz)
Speed	f v (z) = 1 - cos (2πz)
Acceleration	f a (z) = 2π sin(2πz)
Pulse	f j (z) = 4π 2 cos(2πz)

Harmonic (sinusoidal)

Smoothness in velocity and acceleration during the stroke is the advantage inherent in this curve. However, the instantaneous changes in acceleration at the beginning and end of the motion tend to cause vibration, noise and wear.

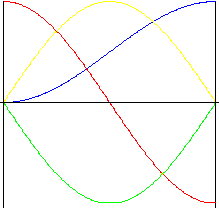
	Lift
	Speed
	Acceleration
	Pulse

Lift	f y (z) = 0.5 (1 - cos πz))
Speed	f v (z) = 0.5 π sin (πz)
Acceleration	f a (z) = 0.5 π 2 cos(πz)
Pulse	f j (z) = -0.5π 3 sin(πz)

Linear

Simple motion with huge shock at start and at end of motion. Rarely used except in very crude devices. We recommend that you use motion with modified start and end of motion – Parabolic with linear part.

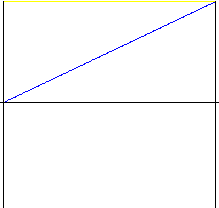
	Lift
	Speed

Lift	f y (z) = z
Speed	f v (z) = 1
Acceleration	f a (z) = 0
	Note: For z = 0 and z = 1 the proper value should be an infinite value, but the calculation cannot work with an infinite value and uses a zero value.
Pulse	f j (z) = 0
	Note: For z = 0 and z = 1 the proper value should be an infinite value but the calculation cannot work with an infinite value and uses a zero value.

Parabolic (Polynomial of 2 ^nd degree)

Motion with smallest possible acceleration. However, because of the sudden changes in acceleration at the start, middle, and end of the motion, shocks are produced. Revese ratio allows “stretch” of middle of motion to allow change in acceleration and deceleration ratio.

symmetrical (reverse ratio k _r = 0.5)

	Lift
	Speed
	Acceleration

	for z = 0 to 0.5:
		Lift	fy(z) = 2z 2
		Speed	fv(z) = 4z
		Acceleration	fa (z) = 4
		Pulse	fa(z) = 0
	for z = 0.5 - 1:
		Lift	fy(z) = 1 - 2(1 - z) 2
		Speed	fv(z) = 4 (1 - z)
		Acceleration	fa (z) = -4
		Pulse	fj(z) = 0
			Note: For z = 0 and z = 1 the proper value should be an infinite value but the calculation cannot work with an infinite value and uses a zero value.

nonsymmetrical

k _r - reverse ratio (in range 0.01 to 0.99)

	Lift
	Speed
	Acceleration

	for z = 0 to k r :
		Lift	f y (z) = z 2 / k r
		Speed	f v (z) = 2z / k r
		Acceleration	f a (z) = 2 / k r
		Pulse	f j (z) = 0
	for z = k r to 1:
		Lift	f y (z) = 1 – (1 – z) 2 / (1 – k r )
		Speed	f v (z) = 2 (1 – z) / (1 – k r )
		Acceleration	f a (z) = -2 / (1 - k r )
		Pulse	f j (z) = 0
			Note: For z = 0 and z = 1 the proper value should be an infinite value but the calculation cannot work with an infinite value and uses a zero value.

Parabolic with linear part

Provide more acceptable acceleration and deceleration than linear motion. Revese ratio allows “stretch” of middle of motion to allow change in acceleration and deceleration ratio. Linear part ratio allows set relative size of linear motion part.

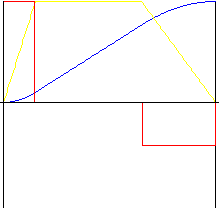
	Speed
	Acceleration
	Pulse

k _r - reverse ratio (in range 0.01 to 0.99)

k _l - linear part ratio (in range 0 to 0.99)

k _z = 1 + k _l / (1 - k _l )

k _h = (1 - k _l ) / (1 + k _l )

	for z = 0 to k r / k z :
		Lift	f y (z) = k h z 2 k z 2 / k r
		Speed	f v (z) = 2 k h z k z 2 / k r
		Acceleration	f a (z) = 2 k h k z 2 / k r
		Pulse	f j (z) = 0
	for z = k r / k z to r / k z + k l :
		Lift	f y (z) = (z - 0.5 k r / k z ) 2 / (1 + k l )
		Speed	f v (z) = 2 / (1 + k l )
		Acceleration	f a (z) = 0
		Pulse	f j (z) = 0
	for z = k r / k z + k l to 1:
		Lift	f y (z) = 1 - k h (1 - z) 2 k z 2 / (1 - k r )
		Speed	f v (z) = 2 k h (1 - z) k z 2 / (1 - k r )
		Acceleration	f a (z) = -2 k h k z 2 / (1 - k r )
		Pulse	f j (z) = 0

Polynomial of 3 ^rd degree (cubic parabola)

Motion with smaller shocks than parabolic motion.

	Lift
	Speed
	Acceleration
	Pulse

Lift	f y (z) = (3 -2z) z 2
Speed	f v (z) = (6 - 6z) z
Acceleration	f a (z) = 6 - 12z
Pulse	f j (z) = -12

Polynomial of 4 ^th degree

Motion with smaller shocks than Polynomial of 3 ^rd degree motion.

	Lift
	Speed
	Acceleration
	Pulse

for z = 0 - 0.5
	Lift	f y (z) = (1 - z) 8z 3
	Speed	f v (z) = (24 - 32z) z 2
	Acceleration	f a (z) = (48 - 96z) z
	Pulse	f j (z) = 48 - 192z
for z = 0.5 - 1
	Lift	f y (z) = 1 - 8z (1 - z) 3
	Speed	f v (z) = (32z - 8) (1 - z) 2
	Acceleration	f a (z) = (48 - 96z) (1 - z)
	Pulse	f j (z) = 194z - 144

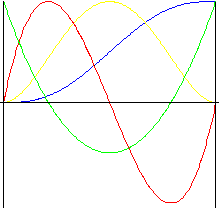
Polynomial of 5 ^th degree

Motion with smaller shocks than Polynomial of 3 ^rd degree motion.

	Lift
	Speed
	Acceleration
	Pulse

Lift	f y (z) = (6z 2 - 15z + 10) z 3
Speed	f v (z) = (z 2 - 2z + 1) 30z 2
Acceleration	f a (z) = (2z 2 - 3z + 1) 60z
Pulse	f j (z) = (6z 2 - 6z + 1) 60

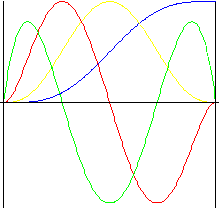
Polynomial of 7 ^th degree

Smoothness in all formulas including pulse.

	Lift
	Speed
	Acceleration
	Pulse

Lift	f y (z) = (-20z 3 + 70z 2 - 84z + 35) z 4
Speed	f v (z) = (-z 3 + 3z 2 - 3z + 1) 140z 3
Acceleration	f a (z) = (-2z 3 + 5z 2 - 4z + 1) 420z 2
Pulse	f j (z) = (-5z 3 + 10z 2 - 6z + 1) 840z

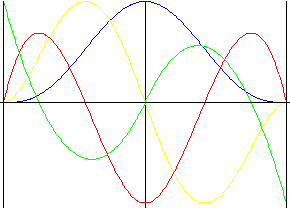
Nonsymmetric Polynomial of 5 ^th degree

Similar like Polynomial of 5th degree but with forced lift reversion.

Note: Require combination of part 1 and part 2.

	Lift
	Speed
	Acceleration
	Pulse

Part 1
	Lift	f y (z) = 1 - (8 (1 - z) 3 - 15 (1 - z) 2 + 10) (1 - z) 2 / 3
	Speed	f v (z) = (2 (1 - z) 3 - 3 (1 - z) 2 + 1) (1 - z) 20 / 3
	Acceleration	f a (z) = -(8 (1 - z) 3 - 9 (1 - z) 2 + 1) 20 / 3
	Pulse	f j (z) = (4 (1 - z) 2 - 3 (1 - z)) 40

Part 2
	Lift	f y (z) = (8z 3 - 15z 2 + 10) z 2 / 3
	Speed	f v (z) = (2z 3 - 3z 2 + 1) z 20/3
	Acceleration	f a (z) = (8z 3 - 9z 2 + 1) 20/3
	Pulse	f j (z) = (4z 2 - 3z) 40

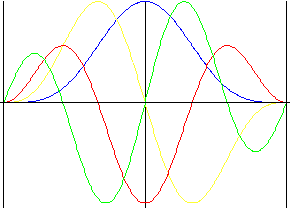
Double Harmonic

Smoothness in all formulas including pulse with forced lift reversion..

Note: Require combination of part 1 and part 2.

Part 1
	Lift	f y (z) = cos(0.5π (1 - z)) 4
	Speed	f v (z) = π (0.5 sin(πz) - 0.25 sin(2πz))
	Acceleration	f a (z) = 0.5 π 2 (cos(πz) - cos(2πz))
	Pulse	f j (z) = π 3 (-0.5 sin(πz) + sin(2πz))

Part 2
	Lift	f y (z) = 1 - cos(0.5π z) 4
	Speed	f v (z) = π (0.5 sin(πz) + 0.25 sin(2πz))
	Acceleration	f a (z) = 0.5 π 2 (cos(πz) + cos(2πz))
	Pulse	f j (z) = -π 3 (0.5 sin(πz) + sin(2πz))

Comparison of maximal relative values

Motion	Speed	Acceleration	Pulse
Cycloidal (extended sinusoidal)	2	6.28	39.5
Harmonic (sinusoidal)	1.57	4.93	15.5
Linear	1	∞	∞
Parabolic (Polynomial of 2 nd degree)	2	4	∞
Polynomial of 3 rd degree	1.5	6	12
Polynomial of 4 th degree	2	6	48
Polynomial of 5 th degree	1.88	5.77	60
Polynomial of 7 th degree	2.19	7.51	52.5
Nonsymmetric Polynomial of 5 th degree	1.73	6.67	40
Double Harmonic	2.04	9.87	42.4

Other dependencies

Force on roller

F i = F + m a i + c y i [N, lb]

Normal Force

Fn i = F i / cos (γ i ) [N, lb]

Moment

T i = F i r i tan (γ i ) [Nmm, lb in]

Specific (Hertz) Pressure

	b = min (b v, b k )