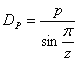The chain length is given by number of chain links and the chain pitch. The chain drive trajectory is based on individual sprocket position and desired direction of motion.
The algorithm to compute chain length uses sprockets pitch diameters. The pitch diameter for each roller chain drive sprocket or idler is obtained from equations below.
The sliding sprocket position is adjusted accordingly to accomplish desired chain length. The calculation uses linear algebra and iteration solution to find appropriate sliding sprocket position.
When the chain length is computed it is taken onto account that the trajectory is composed from linear segments at chain pitch length and arcs are replaced with actual polygons.
Pitch diameters
 |
|
|
|
where: |
||
|
D P |
Pitch diameter |
|
|
p |
chain pitch |
|
|
z |
number of sprocket teeth |
|
|
|
D p = D + D r |
|
|
where: |
||
|
D P |
Pitch diameter |
|
|
D |
Nominal idler diameter |
|
|
D r |
maximum chain roller diameter |
|
Example of chain drive with two sprockets
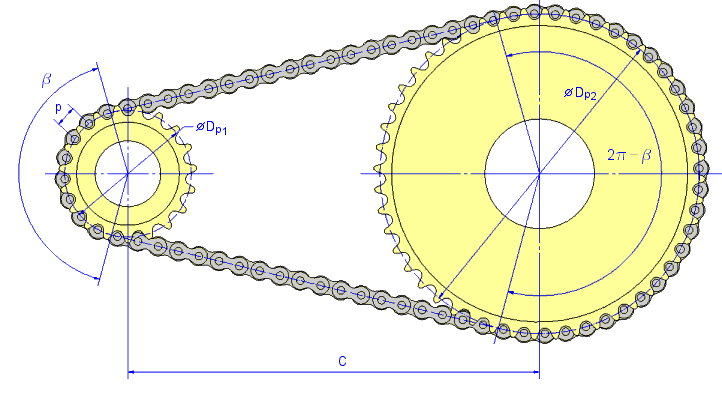
Required number of chain links for desired center distance
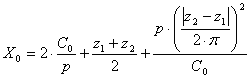
The required number of chain links is rounded to closest even or odd number and then the actual center distance is then determined as
C = F p [ 2 X - (z 1 + z 2 )]
where:
|
|
|
|
|
Contact angle is determined as
|
|
Number of teeth in contact of the small sprocket
|
|
Meaning of used variables:
|
C 0 |
Desired center distance [m] |
|
C |
Actual center distance [m] |
|
p |
Chain pitch [m] |
|
z 1 |
Number of teeth of the driver sprocket [-] |
|
z 2 |
Number of teeth of the driven sprocket [-] |
|
D P1 |
Pitch diameter of the driver sprocket [m] |
|
D P2 |
Pitch diameter of the driven sprocket [m] |
|
X 0 |
Required number of chain links [-] |
| β |
Contact angle [deg] |