General Calculation Formulas
Utilization factor of material
Safety factor at the fatigue limit
Outside spring diameter
D 1 = D + d [in]
where:
|
D |
mean spring diameter [in] |
|
|
d |
wire diameter [in] |
Inside spring diameter
D 2 = D - d [in]
where:
|
D |
mean spring diameter [in] |
|
|
d |
wire diameter [in] |
Working deflection
H = L 1 - L 8 = s 8 - s 1 [in]
where:
|
L 8 |
length of fully loaded spring [in] |
|
|
L 1 |
length of pre loaded spring [in] |
|
|
s 8 |
deflection of fully loaded spring [in] |
|
|
s 1 |
deflection of pre loaded spring [in] |
Spring index
c = D/d [-]
where:
|
D |
mean spring diameter [in] |
|
|
d |
wire diameter [in] |
Wahl correction factor
![]()
where:
|
c |
spring index [-] |
General force exerted by the spring
![]()
where:
|
d |
wire diameter [in] |
|
| τ |
torsional stress of spring material in general [psi] |
|
|
D |
mean spring diameter [mm] |
|
|
K w |
Wahl correction factor [-] |
|
|
G |
modulus of elasticity of spring material [psi] |
|
|
s |
spring deflection in general [in] |
|
|
n |
number of active coils [-] |
|
|
F 0 |
spring initial tension [N] |
Spring constant
![]()
where:
|
d |
wire diameter [in] |
|
|
D |
mean spring diameter [mm] |
|
|
G |
modulus of elasticity of spring material [psi] |
|
|
n |
number of active coils [-] |
|
|
F 8 |
working force in fully loaded spring [psi] |
|
|
F 1 |
working force in minimum loaded spring [psi] |
|
|
H |
working deflection [in] |
Mean spring diameter
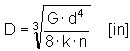
where:
|
G |
modulus of elasticity of spring material [psi] |
|
|
d |
wire diameter [mm] |
|
|
k |
spring constant [lb/in] |
|
|
n |
number of active coils [-] |
Spring deflection in general
s = F / k [in]
where:
|
F |
General force exerted by the spring [lb] |
|
|
k |
spring constant [lb/in] |
Loose spring length
L 0 = L 1 + s 1 = L 8 + s 8 [in]
where:
|
L 8 |
length of fully loaded spring [in] |
|
|
L 1 |
length of pre loaded spring [in] |
|
|
s 8 |
deflection of fully loaded spring [in] |
|
|
s 1 |
deflection of pre loaded spring [in] |
Spring Design Calculation
Design the wire diameter, number of coils and spring free length L 0 for a specific load, material, and assembly dimensions or spring diameter. With the recommended wire diameters, the t pitch between spring threads in free state is within the 0.3 D ≤ t ≤ 0.6 D [in] range.
Base the spring on the τ 8 ≤ u s τ A strength condition and the recommended ranges of some spring geometric dimensions:
L 8 ≥ L minF and D ≤ L 0 ≤ 10 D and L 0 ≤ 31.5 in and 4 ≤ D/d ≤ 16 and n≥ 2 and 12 d ≤ t < D
where:
|
D |
mean spring diameter [in] |
|
|
d |
wire diameter [in] |
|
| τ |
pitch of active coils in free state [in] |
|
|
τ 8 |
torsional stress of spring material in the fully loaded stress [psi] |
|
|
τ A |
allowable torsion stress of spring material [psi] |
|
|
u s |
utilization factor of material [-] |
|
|
L 8 |
length of fully loaded spring [in] |
|
|
L minF |
limit test length of spring [in] |
|
|
n |
number of active coils [-] |
Comply with the safety conditions for buckling, and check the specification for conditions for fatigue loading.
Design Procedures
1. Specified load, material, and spring assembly dimensions
First check and calculate the input values.
Design the wire diameter and number of coils in accordance with the strength and geometric requirements listed previously, or use spring diameter values in the specification.
During the design the program calculates, step by step from the smallest to the biggest, all the spring wire diameters that conform to the strength and geometric conditions. If all conditions are fulfilled, the design is finished with selected values, irrespective of other conforming spring wire diameters. This means that the program tries to design a spring with the least wire diameter and the least number of coils.
2. Spring design for a specified load, material, and spring diameter
First, check the input values for the calculation.
Design the wire diameter, number of coils, spring free length, and assembly dimensions in accordance with the strength and geometric conditions previously listed, or with any assembly dimension L 1 or L 8 stated in the specification, or any working spring deflection value that is limited.
Use the following formula to design the spring for the specified wire diameter.

where:
|
τ 8 = 0.85 τ A |
||
|
F 8 |
working force in fully loaded spring [psi] |
|
|
D |
mean spring diameter [in] |
|
|
K w |
Wahl correction factor [-] |
|
|
τ 8 |
torsional stress of spring material in the fully loaded stress [psi] |
|
|
τ A |
allowable torsion stress of spring material [psi] |
|
If no suitable combination of spring dimensions can be designed for this wire diameter, all the spring wire diameters that conform to the strength and geometric conditions are tested, starting with the smallest, going up to the biggest. The suitable coil numbers are tested, whether the spring design conforms with the conditions. In this case the design is finished with the selected values, irrespective of other suitable spring wire diameters, and the spring is designed with the least wire diameter and the least number of coils.
3. Spring design for the specified maximum working force, determined material, assembly dimensions, and spring diameter
First, check the input values for the calculation.
Then the wire diameter, number of coils, spring free length, and the F 1 minimum working force are designed in accordance with the strength and geometric conditions listed previously.
Use the following formula to design the spring for the specified wire diameter.

where:
|
τ 8 = 0.85 τ A |
||
|
F 8 |
working force in fully loaded spring [psi] |
|
|
D |
mean spring diameter [in] |
|
|
K w |
Wahl correction factor [-] |
|
|
τ 8 |
torsional stress of spring material in the fully loaded stress [psi] |
|
|
τ A |
allowable torsion stress of spring material [psi] |
|
If no suitable combination of spring dimensions can be designed for this wire diameter, all the spring wire diameters that conform to the strength and geometric conditions are tested, starting with the smallest, going up to the biggest. The suitable coil numbers are tested, whether the spring design conforms with the conditions. In this case the design is finished with the selected values, irrespective of other suitable spring wire diameters, and the spring is designed with the least wire diameter and the least number of coils.
Spring Check Calculation
Calculates corresponding values of assembly dimensions and working deflection for the specified load, material, and spring dimensions.
First, the input values for the calculation are checked. Then the assembly dimensions are calculated using the following formulas.
Length of preloaded spring
![]()
Length of fully loaded spring
![]()
where:
|
L 0 |
length of free spring [in] |
|
|
F 1 |
working force in minimum loaded spring [in] |
|
|
n |
number of active coils [-] |
|
|
D |
mean spring diameter [in] |
|
|
G |
modulus of elasticity of spring material [psi] |
|
|
d |
wire diameter [in] |
|
|
F 8 |
working force in fully loaded spring [psi] |
Working deflection
H = L 1 - L 8 [in]
Calculation of Working Forces
Calculates corresponding forces produced by springs in their working states for the specified material, assembly dimensions, and spring dimensions. First the input data is checked and calculated, and then the working forces are calculated using to the following formulas.
Minimum working force
![]()
Maximum working force
![]()
Calculation of spring output parameters
Common for all types of spring calculation, and calculated in the following order.
Spring constant
![]()
Theoretic limit length of spring
L 9 = (n + n z + 1 - z 0 ) d [in]
Limit test length of spring
L minF = L 9max + S amin [in]
where the upper limit spring length in the limit state L 9max :
|
for non ground ends |
|
|
L 9max = 1.03 L 9 [in] |
|
|
for ground ends and (n + nz) <= 10.5 |
|
|
L 9max = (n + n z ) d [in] |
|
|
for ground ends and (n + nz) > 10.5 |
|
|
L 9max = 1.05 L 9 [in] |
|
Sum of the least allowable space between spring active coils in the fully loaded state
![]()
while the c = 5 value is used for the c < 5 spring index values
Spring deflection in limit state
s 9 = L 0 - L 9 [in]
Limit spring force
F 9 = k S 9 [lb]
Space between coils
![]()
Pitch of active coils
t = a + d [in]
Pre loaded spring deflection
s 1 = L 0 - L 1 [in]
Total spring deflection
s 8 = L 0 - L 8 [in]
Torsional stress of spring material in the pre loaded state
![]()
Torsional stress of spring material in the fully loaded stress
![]()
Solid length stress
![]()
Developed wire length
l = 3.2 D (n + n z ) [in]
Spring mass
![]()
Spring deformation energy
![]()
Natural frequency of spring surge
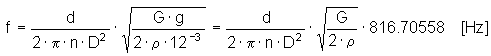
Critical (limit) spring speed concerning the arousal of mutual coil impacts from inertia
![]()
Check of spring load
τ 8 ≤ u s τ A and L minF ≤ L 8
Meaning of used variables:
|
a |
space between active coils in the free state [in] |
|
k |
spring constant [lb/ft] |
|
d |
wire diameter [in] |
|
D |
mean spring diameter [in] |
|
D 1 |
spring outside diameter [in] |
|
D 2 |
spring inside diameter [in] |
|
F |
general force exerted by the spring [lb] |
|
G |
shear modulus of elasticity of spring material [psi] |
|
c |
spring index [-] |
|
H |
working deflection [in] |
|
K w |
Wahl correction factor [-] |
|
k f |
safety factor at the fatigue limit [-] |
|
l |
developed wire length [in] |
|
L |
spring length in general [in] |
|
L 9max |
upper limit length of spring in the limit state [in] |
|
L minF |
limit test length of spring [in] |
|
m |
spring mass [lb] |
|
N |
life of fatigue loaded spring in thousands of deflections [-] |
|
n |
number of active coils [-] |
|
n z |
number of end coils [in] |
|
t |
pitch of active coils in free state [in] |
|
s |
spring deflection (elongation) in general [in] |
|
s amin |
sum of the least allowable space between spring active coils [in] |
|
u s |
utilization factor of material [-] |
|
z 0 |
number of ground coils [-] |
| ρ |
density of spring material [lb/ft 3 ] |
|
σ ult |
ultimate tensile stress of spring material [psi] |
| τ |
torsional stress of spring material in general [psi] |
|
τ e |
endurance limit in shear of fatigue loaded spring [psi] |
|
τ A8 |
allowable torsion stress of spring material [psi] |