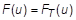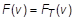Rod Type Spring and Damper Property
Description: Defines linear and nonlinear properties of a one-dimensional spring and damper element (CBUSH1D entry).
Format:

Example:

| Field | Definition | Type | Default |
|---|---|---|---|
| PID | Property identification number. | Integer > 0 | Required |
| K | Stiffness. See Remark 1. | Real | |
| C | Viscous damping. See Remarks 1 and 2. | Real | |
| M | Total element mass. | Real | |
| SA | Stress recovery coefficient. | Real | 1.0 |
| SE | Strain recovery coefficient. | Real | 1.0 |
| SPRING | Character string specifying that the TID in field 4 defines a nonlinear elastic spring element in terms of a force versus displacement relationship.
|
Character | |
| DAMPER | Character string specifying that the TID in field 4 defines a nonlinear viscous element in terms of a force versus velocity relationship.
|
Character | |
| TID | Identification number of a TABLEDi entry for tension and compression. | Integer > 0 | Required for SPRING or DAMPER |
Remarks:
- Either the stiffness K or the damping C must be specified.
- The damping C and mass M are ignored in static solution sequences.
- The parameters defined on the continuation entries are used in nonlinear solution sequences only.
- The linear parameters K and C are used in all solution sequences unless parameters on continuation entries are defined and a nonlinear solution sequence is used. Then, the parameters K and C are used for initial values in the first iteration of the first load step and the parameters from continuation entries overwrite the linear parameters thereafter. When SPRING is specified, K is overwritten. When DAMPER is specified, C is overwritten. K and/or C should be non-zero if SPRING and/or DAMPER is specified otherwise the respective table will be ignored.
- Values on the TABLEDi entry are for tension and compression. If table values
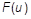 are provided only for positive values
u > 0, then it is assumed that
are provided only for positive values
u > 0, then it is assumed that
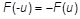 .
.
- The element stresses are computed by multiplying the stress coefficient with the recovered element force.
- The element strains are computed by multiplying the strain coefficient with the recovered element displacement.
- The SPRING and DAMPER may be specified in any order.