Select from the following types of slab geometry and parameters:
|
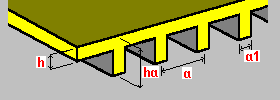
One-sided unidirectional ribs: h - plate thickness ha - rib height a - rib spacing a1 - rib width |

|
Double-sided unidirectional ribs: h - plate thickness ha - rib height a - rib spacing a1 - rib width |
|
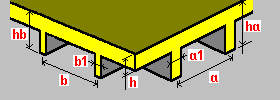
One-sided bi-directional ribs: h - plate thickness ha - rib height hb - rib height a - rib spacing a1 - rib width b - rib spacing b1 - rib width |
|
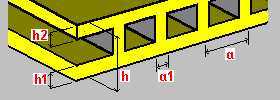
Unidirectional box floor: h - floor thickness h1 - lower plate thickness h2 - upper plate thickness a - rib spacing a1 - rib width |

|
Bi-directional box floor: h - floor thickness h1 - lower plate thickness h2 - upper plate thickness a - rib spacing a1 - rib width b - rib spacing b1 - rib width |

|
Grillage: h - rib height a - rib spacing a1 - rib width b - rib spacing b1 - rib width |
|
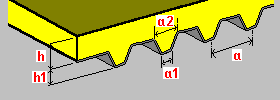
Slab on trapezoidal plate: h - plate thickness h1 - steel plate height a - steel plate rib spacing a1 - bottom rib width a2 - top rib width |
|
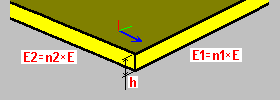
Material orthotropy: h - plate thickness n1 - stiffness coefficient n2 - stiffness coefficient |
|
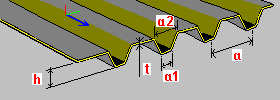
Trapezoidal plate: h - plate height t - plate thickness a, a1, a2 - dimensions of a single plate segment (spacing, width values) |
|
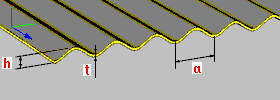
Corrugated plate: h - plate height t - plate thickness a - dimension of a single plate segment (spacing) |
|
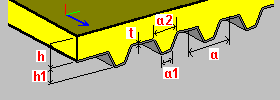
Slab composed with a trapezoidal plate h - slab thickness h1 - plate height t - plate thickness a, a1, a2 - dimensions of a single plate segment (spacing, widths) Es - Young's modulus (trapezoid steel) vs - Poisson's ratio (trapezoid steel) Eb - Young's modulus (concrete; a value adopted based on a selected material) vb - Posson's ratio (concrete; a value adopted based on a selected material) |

|
Constant thickness with reduced stiffness: h - slab thickness coefficients of reduction of the matrix elements: membrane stiffness D, flexure stiffness K and shear stiffness H; additionally, it is possible to define a coefficient of weight reduction taken into account during generation of a self-weight load; values of these coefficients are defined in the Coefficients of Stiffness, Weight, Mass dialog that opens after clicking Coefficients. |
|
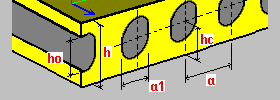
Hollow slab (with circular or oval openings) h - slab thickness a - stiffener spacing, opening spacing a1 - opening width / circle diameter ho - opening height (slab with oval openings) hc - distance between the opening center and the slab edge h1 - lower flange height of the slab h2 - upper flange height of the slab (h2 = h - hc - c/2 - a1/2) c = ho - a1 (slab with oval openings) The Disregard transversal bending stiffness option allows to omit or consider bending stiffness K_YYYY in calculations. Disregarding bending stiffness (Y direction) aims at better modeling of the precast hollow slabs. |
The material orthotropy introduces diversified plate stiffness resulting from different physical properties in perpendicular directions. A stiffness difference is determined by means of the modified Young's moduli E1, E2, respectively, in the selected orthotropy direction x, y. The moduli E1, E2 are a product of a selected material and the user-defined coefficients n1, n2. For both directions, constant Poisson's ratio is adopted. This type of orthotropy can be used to create a model of RC slabs with bi-directional reinforcement.
The stiffness coefficient for RC slabs with bi-directional reinforcement can be defined on the basis of the following formula. Assuming that the slab material is linearly elastic, the stiffness coefficient for the direction parallel to the reinforcement direction equals:
n = 1+ 12/(h*h) * e*e * m * u / (1+ m*u)
where:
h is the height of a slab section.
m = Ez/Eb is the ratio of steel and concrete Young's modulus.
e is the distance between reinforcement gravity center and the middle plane of a slab.
u is the reinforcement ratio, expressed as a decimal fraction (a section area of reinforcement bars referred to a unit area of a slab section).
See also: