Parámetros del análisis sísmico (norma australiana AS 1170-4:2007)

Los parámetros del análisis sísmico simplificado según el método del esfuerzo lateral equivalente dependen de la norma sísmica y el modo de definir los valores de los periodos fundamentales seleccionados en el cuadro de diálogo Análisis sísmico.

Método aproximado

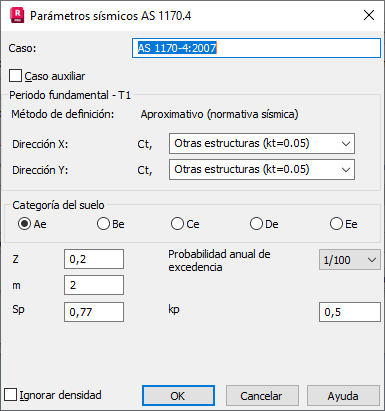
El período fundamental T1 se calcula según la ecuación 6.2(7):

T₁ = 1.25 * k_t * h_n ^0.75

donde:

k_t es el coeficiente para determinar el periodo de construcción (proporcionado por la norma).

h es la altura de la estructura (m), definida por la diferencia entre el rango de la estructura y el nivel de referencia.

Método definido por el usuario

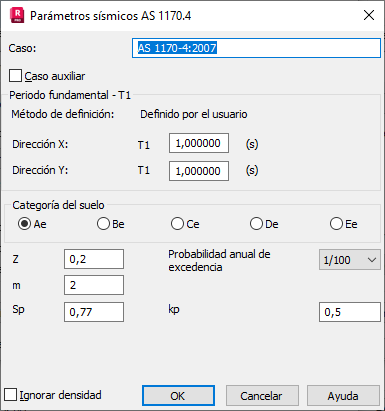
Solo se debe definir T1 en ambas direcciones.

Método exacto

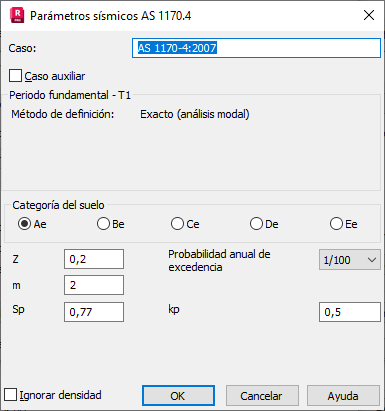
Según este método, se puede calcular el valor exacto de las direcciones X e Y. Si la opción Periodos con participación de masas máxima está desactivada en el cuadro de diálogo Análisis sísmico, estará activo el primero modo en la dirección en la que haya más masas. Si esta opción está activada, uno de los modos, que cumplen las limitaciones y la mayoría de las masas, estará activo en la dirección.

Parámetros normativos

• Categoría del suelo según se define en las cláusulas 4.1.
• Valores de los coeficientes: Z (coeficiente de riesgo), tabla 3.2, (coeficiente de ductilidad estructural) y S_p (coeficiente de rendimiento estructural), como se indica en la cláusula 6.5.
• Probabilidad anual de excedencia y coeficiente kp (coeficiente de probabilidad), tabla 3.1.

Cortante básico

El esfuerzo cortante básico se calcula según la siguiente fórmula:

V = [k_p*Z*C_h(T₁)*S_p/μ]/W _t (eq. 6.2(3))

Donde:

K_p es un coeficiente de probabilidad (tabla 3.1) que depende de la probabilidad anual de excedencia (P).

Z es un coeficiente de riesgo y se obtiene de la tabla 3.2.

C_h (T1) se calcula sobre la base de la tabla 6.4.

μ y S_p son los valores de la tabla 6.5.

W_t es el peso de la estructura.

La distribución del esfuerzo cortante básico se realiza según la siguiente fórmula:

F_x = V * W_i * h^k _i / (Σ W_i * h^k _i) (eq. 6.3(2))

i=1..storeysCount

W_i y W_j hacen referencia al peso del suelo.

h es la altura desde el nivel base hasta el nivel de suelo adecuado.

V es el esfuerzo cortante básico.

k es un exponente que depende del valor de periodo, como se muestra a continuación:

Periodo (T1)	k
< 0,5 s	1
0,5 - 2,5 s	Interpolación lineal
> 2,5 s	2