La ecuación del flujo de calor dentro del contorno que se muestra más abajo puede presentarse como se indica a continuación.
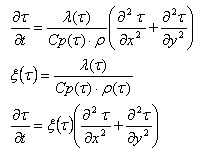
donde:
Cp : calor específico (J/kg*K)
λ: conductividad térmica (W/m*K)
ρ: peso unitario (kg/m3)
En la notación diferencial, las ecuaciones de flujo de calor se pueden escribir como se indica a continuación:
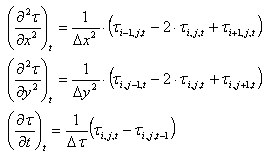 .
.
Estas ecuaciones producen lo siguiente:
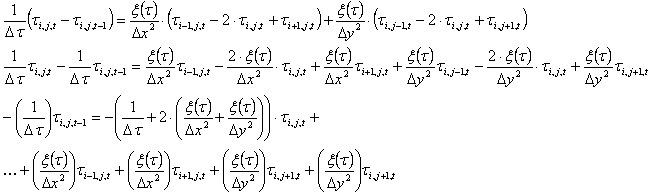 .
.
Por lo tanto, para los nudos K, se resolverá el sistema de ecuaciones M[KxK] x τ[K] = B[K].
Aproximaciones adoptadas
Cuando se necesita conocer la temperatura actual para determinar los coeficientes no descritos por las ecuaciones, se aplica la aproximación de los pasos del tiempo anteriores (diferencia de avance).
Para el paso del tiempo constante Δτ, se obtiene lo siguiente:
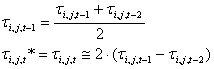
que permite determinar lo siguiente:
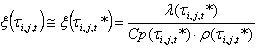
para el paso i = 1 t i,j,1 * = t i,j,o.
Condiciones de contorno
Para la formulación general del problema, se añaden condiciones de contorno de tercer tipo que son responsables de lo siguiente:
- Convección
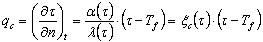
donde:
n: normal al borde
Tf: temperatura en el entorno exterior del contorno identificada con la temperatura de incendio.
Suponiendo que el coeficiente de convección a sea independiente de la temperatura y adopte las aproximaciones antes mencionadas, se obtiene lo siguiente:
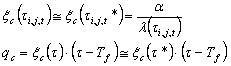 .
. - Radiación
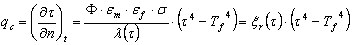
donde:
n: normal al borde
Tf: temperatura en el entorno exterior del contorno identificada con la temperatura de incendio
Φ: coeficiente de configuración
εm: coeficiente de emisión del elemento
εf: coeficiente de emisión del fuego
σ: constante de Boltzman 5.65*10 8 (W/m 2 *K 4 )
Adoptando las aproximaciones mencionadas anteriormente, se obtiene lo siguiente:
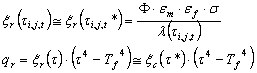 .
.
Hipótesis utilizada para la norma DTU P 92-701
- Desarrollo de fuego en el tiempo
El fuego se describe en forma discreta (tabular) en función de la siguiente fórmula:
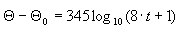 (sección 4 DTU P 92-701, figura 11)
(sección 4 DTU P 92-701, figura 11) El fuego se describe en forma discreta (tabular) en función de la siguiente fórmula:
donde t se expresa en [min]
que permite describir la temperatura del fuego como se indica a continuación:
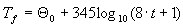
Los valores discretos se seleccionan de forma que no se produce ningún aumento de temperatura superior al 30 % en ningún incremento de tiempo. La interpolación lineal se realiza entre estos valores.
En el archivo Fire_DTU.t se incluye una descripción del desarrollo del fuego en el tiempo.
- Conductividad térmica del hormigón
La dependencia de la conductividad térmica se presenta en forma tabular (sección 3,15 DTU P 92-701).
En el archivo Lambda_DTU.la, se proporciona una descripción del comportamiento de conductividad térmica en función de la temperatura.
- Peso unitario del hormigón
Es independiente de la temperatura y es igual a 2400 [kg/m3].
En el archivo Ro_DTU.cp, se proporciona una descripción del comportamiento del peso unitario en función de la temperatura.
- Calor específico del hormigón
Es independiente de la temperatura y es igual a 921.096 [J/kg *K], es decir, 0.22 [kcal/kg * OC] (sección 3.16 DTU P 92-701).
En el archivo Cp_DTU.cp, se proporciona una descripción del comportamiento de calor específico en función de la temperatura.
- Coeficiente de reducción de la capacidad de hormigón
El coeficiente de reducción de la capacidad de hormigón se presenta en forma tabular (sección 3.13 DTU P 92-701).
En el archivo fic_DTU.cfc, se proporciona una descripción del comportamiento de la reducción de la capacidad de hormigón en función de la temperatura.
- Coeficiente de reducción de la capacidad de acero
El coeficiente de reducción de la capacidad de acero se presenta en forma tabular (sección 3.13 DTU P 92-701).
En el archivo fiy_DTU_1_2.cfy, se proporciona una descripción del comportamiento de la reducción de la capacidad de acero en función de la temperatura.
En el caso de que se utilicen los tipos de acero 3 y 4, establezca el archivo fiy_DTU_3_4.cfy en lugar de uno por defecto.
- Parámetros de cálculo
Coeficientes de radiación:
Φ*εm*εf = 0.85 de forma análoga al coeficiente (sección 4 DTU P 92-701)
Los coeficientes anteriores deben entenderse de la siguiente forma:
Φ: coeficiente de configuración
εm: coeficiente de emisión del elemento
εf: coeficiente de emisión del fuego
Coeficiente de convección:
α = 6.9 [W/m2*K] = 6.0 [kcal/m2*h*oC] (sección 4 DTU P 92-701)
Hipótesis utilizada para la norma EN 1992-1-2
- La evolución del fuego según la norma EN 1991-1-2
El fuego se describe en forma tabular discreta según la siguiente fórmula:
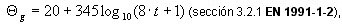
donde:
t expresado en [min]
presuponiendo la temperatura inicial 20 [0C],
que permite describir la temperatura del fuego como se indica a continuación:
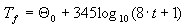 .
. Los valores discretos se seleccionan para que no se produzca ningún aumento de temperatura superior al 30 % en ningún incremento de tiempo. La interpolación lineal se realiza entre estos valores.
En el archivo Fire_EC2_N.t., se incluye una descripción del desarrollo del fuego en el tiempo.
En el caso de que se utilicen otros tipos de fuego, en lugar de un archivo por defecto, establezca lo siguiente:
Fuego externo (sección 3.2.2 EN 1991-1-2): Fire_EC2_E.t
Fuego de hidrocarburos (sección 3.2.3 EN 1991-1-2): Fire_EC2_H.t
- Conductividad térmica del hormigón
La dependencia de la conductividad térmica se presenta en forma tabular (sección 3.4 EN 1992-1-2), sobre la base del valor inferior de conductividad térmica. La interpolación lineal se realiza entre estos valores.
En el archivo Lambda_EC2_L.la, se incluye una descripción del comportamiento de conductividad térmica en función de la temperatura.
En el caso de que se utilice el valor superior, en lugar de un archivo por defecto, el usuario debe establecer lo siguiente:
Lambda_EC2_U.la
- Peso unitario del hormigón
La dependencia del peso unitario se presenta en forma tabular, sección 3.3.2(3) EN 1992-1-2. La interpolación lineal se realiza entre estos valores.
En el archivo Ro_EC2.cp, se incluye una descripción del comportamiento del peso unitario en función de la temperatura.
- Calor específico del hormigón
La dependencia de calor específico se presenta en forma tabular, sección 3.3.2(1) y 3.3.2(2) EN 1992-1-2, sobre la base de los valores de humedad del 1.5 %. La interpolación lineal se realiza entre estos valores.
En el archivo Cp_EC2_m015.cp, se incluye una descripción del comportamiento de calor específico en función de la temperatura.
En el caso de que se utilicen otros valores de humedad del hormigón, en lugar de un archivo por defecto, establezca lo siguiente:
0 % de humedad: Cp_EC2_m000.cp
3 % de humedad: Cp_EC2_m030.cp
- Coeficiente de reducción de la capacidad de hormigón
La dependencia del coeficiente de reducción de la capacidad de hormigón se presenta en forma tabular (sección 4.2.4.2 EN 1992-1-2) sobre la base de los valores para el hormigón con agregado de silicato. La interpolación lineal se realiza entre estos valores.
En el archivo fic_EC2_Si.cfc, se incluye una descripción del comportamiento de la reducción de la capacidad de hormigón en función de la temperatura.
En el caso de que se utilice hormigón con agregado de caliza, en lugar de un archivo por defecto, establezca lo siguiente: fic_EC2_Ca.cfc.
- Coeficiente de reducción de la capacidad de acero
La dependencia del coeficiente de reducción de la capacidad de acero se presenta en forma tabular (sección 3.2.3 EN 1992-1-2) en función de los valores para acero de clase N laminado en caliente. La interpolación lineal se realiza entre estos valores.
En el archivo fiy_EC2_Nhr.cfy, se incluye una descripción del comportamiento de la reducción de la capacidad de acero en función de la temperatura.
En el caso de que se utilicen otros tipos, en lugar de un archivo por defecto, establezca lo siguiente:
Acero de clase N laminado en frío: fiy_EC2_Ncw.cfy.
Acero de clase X: fiy_EC2_X.cfy.
- Parámetros de cálculo
Coeficientes de radiación:
Φ = 1.0: coeficiente de configuración (sección 3.1(6) EN 1991-1-2)
εm = 0.8: coeficiente de emisión del elemento (sección 3.1(6) EN 1991-1-2)
εf = 1.0: coeficiente de emisión del fuego (sección 3.1(6) EN 1991-1-2)
Coeficiente de convección:
αce = 25 [W/m2*K] en el lado expuesto al fuego (sección 3.2.1 EN 1991-1-2)
αcu = 9.0 [kcal/m2*h*oC] en el lado no expuesto al fuego (sección 3.1(5) EN 1991-1-2)
Cálculo de capacidad para la norma BAEL: columnas comprimidas axialmente
Datos necesarios para los cálculos:
fcj: la resistencia del hormigón se transfiere automáticamente desde el módulo de pilares de hormigón armado de Robot.
Φb: coeficiente para el hormigón según la temperatura Φ b (τ), en este caso, τ es una temperatura media dentro de la sección.
f e: la resistencia del acero se transfiere automáticamente desde el módulo de pilares de hormigón armado de Robot.
φsi: coeficiente de acero según la temperatura φ s (τ), en este caso, τ es una temperatura en la barra en la posición i.
l: altura de pilar
N: carga máxima aplicada al pilar
α: coeficiente transferido automáticamente desde el módulo de pilares de hormigón armado

B r = A c - 0.01*u c
Br: área de sección reducida
Ac: área de sección
u c : perímetro de sección
γb: coeficiente de hormigón 1.3
γs: coeficiente de acero 1.0
A i : área de la barra de armadura en la posición i
Capacidad del pilar:
N/NQ > 1.0