Voici la procédure de calcul du coefficient K.
- Le sol sous la semelle est divisée en bandes de 0,2 m d'épaisseur. Si l'épaisseur des couches est inférieure à 0,2 m, les calculs sont effectués pour la couche entière.
- Chaque couche n est analysée sur la base des valeurs calculées à la profondeur étant le centre de la couche Zn
- Pour la profondeur Zn, la contrainte moyenne causée par des charges externes par le poids d'une semelle et la terre sus-jacente ((σ(z)) sous la semelle est déterminée à partir de la formule présentée ci-dessous.
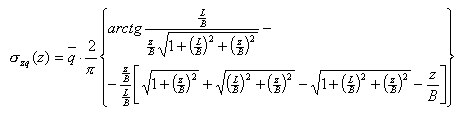
où :
B – Dimension transversale d'un rectangle (semelle)
L – Dimension longitudinale d'un rectangle (semelle)
La formule ci-dessus décrit la valeur moyenne des contraintes en dessous d'une zone rectangulaire. Elle provient de la formule de Boussinesque qui décrit la répartition des contraintes dans le demi-espace élastique dues à la charge par force concentrée.
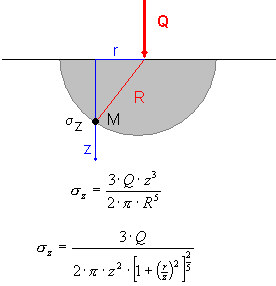
En vous servant du principe de superposition, vous pouvez calculer la contrainte au point P(0,0,z) due à une couche quelconque sollicitée par une charge uniforme, conformément au principe suivant.
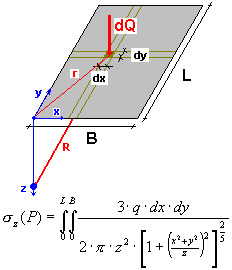
Les solutions de l’équation ci-dessus pour les points de coin de la zone rectangulaire, au-dessous du centre de la surface rectangulaire et la valeur moyenne au-dessous de la zone rectangulaire sont données dans la littérature. Pour obtenir une valeur des contraintes moyennes sous la zone rectangulaire, utilisez la formule suivante. Après l'intégration, il prend la forme appliqué dans l'algorithme de calcul.
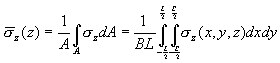
- Pour la profondeur Zn, on définit une contrainte primaire provenant des terres situées sous la couche analysée.
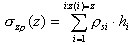Remarque : En cas de présence d'eaux phréatiques, la poussée d’Archimède de l’eau et son poids sont pris en compte dans les calculs. - Des contraintes supplémentaires dans le sol, prise en compte dans les calculs de tassement, sont les contraintes dues à la charge externe.
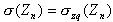
- A partir de la caractéristique du sol, on calcule le tassement moyen de la couche n.
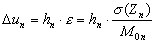
où :
M0n – Il s'agit du module primaire (sans prise en compte des effets de détente), endométrique (obtenu dans l’appareil d'effort triaxial) de compressibilité du sol dans la n-ième couche. Une relation entre le module Young et le module de compressibilité endométrique est exprimée par la formule suivante.
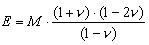Remarque : Si la valeur du module de Poisson est absente pour le type de sol donné, les bases de sols pour un pays donné peuvent contenir les valeurs E = M, ce qui correspond au matériau à compressibilité idéale (n = 0.0). Les valeurs typiques du module de Poisson sont égales à 0.2÷0.3 pour les sols incohérents (la valeur 0.2 concerne les sols à gros grain, comme les graviers, alors que 0.3 concerne les sols à grain fin, comme des poudres) et 0.25÷0.37 pour les sols cohérents (la valeur 0.25 concerne les sols consolidés, alors que 0.37 concerne les sols limoneux).La compression totale du sol est la somme des compressions des couches successives.
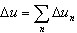
Les calculs sont effectués jusqu'à atteindre le niveau Zn :
- Qui n'est pas inférieur à 1 (m).
- Pour ces contraintes dues à un compte de charge estimée pour moins de 25 % de contraintes causées par le poids du sol.
- Pour cet incrément de tassement de couche, ∆un dans la couche suivante est inférieur à 0,1 % du tassement total
- Qui n'est pas supérieur à 10 (m).
Le coefficient de rigidité calculée s'élève à K = 1 / ∆u. Le coefficient de rigidité K correspond à la charge de l'unité de surface.