Calculs de la qualité des triangles en tant qu’éléments du maillage
Lors de la génération du maillage triangulaire, il faut essayer d’atteindre un tel maillage dont les éléments soient les triangles équilatéraux. Chaque autre triangle, et en particulier le triangle obtusangle, est un maillage "mauvais" du point de vue de la méthode EF.
En admettant que le coefficient de qualité du maillage triangulaire est compris entre <0,1>, le coefficient α égale 1 pour le triangle équilatéral.
Le coefficient α du triangle ayant les sommets ABC est calculé d'après la formule suivante :
L’algorithme est basé sur le calcul du produit vectoriel de deux vecteurs dans l’espace.
Calculs de la qualité des quadrangles en tant qu’éléments du maillage
Le procédé est similaire, en prenant en considération le fait que le quadrangle idéal est le rectangle. Une méthode de calcul des coefficients de triangle est utilisée pour calculer le coefficient α.
Toute forme quadrangulaire ABCD est divisée en quatre triangles superposés (ABC, ACD, ABD et BCD). Le calcul des coefficients α est effectuée pour les triangles particuliers : { α1, a2, α3, α4} = { α (ABC), α (ACD), α (ABD), α (BCD)}. Une fois ces coefficients calculés, nous procédons à calculer le coefficient de qualité pour le quadrangle:
temp1 = α1 * α3;
temp2 = α2 * α4;
if( temp1 * temp2 != 0 )
α= ( temp1 > temp2 ) ? temp2 / temp1 : temp1 / temp2;
α_rect = 0,86602540000000;
α_avg = (α_rect - fabs((α1 + α2 + α3 + α4) / 4. - α_rect))/ α_rect;
if (α_avg < α) α= α_avg;
Calculs du coefficient de qualité global du maillage
Il existe deux manières de calculer le coefficient global:
- on détermine la moyenne de toutes les mailles (triangles, quadrangles) :
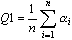
Où n - nombre d'éléments du maillage
- On détermine la qualité moyenne "pondérée" de tous les éléments du maillage (triangles, quadrangles), le critère de poids est la surface d'un élément du maillage:
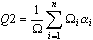
où n - nombre d'éléments du maillage, Ω - surface