Principes théoriques des méthodes utilisées lors de l’analyse dynamique de la structure

Introduction

Ce document décrit les méthodes d'analyse dynamique appliquées dans Robot. On trouvera les modalités théoriques et plusieurs exemples dans les annexes. Cette rubrique n'a aucune prétention éducative et n'entend pas expliciter l'interface de Robot. Elle énumère les principes sur lesquels reposent ce programme.

La plupart des méthodes dynamique de Robot reposent les résultats d'analyses modales. Il faut bien comprendre que les méthodes d'analyse modale dépendent du type de solveur retenu. Pour le solveur Skyline, on dispose des méthodes suivantes : Itération dans le sous-espace par blocs (BLSI), Itération sur sous-espace (SI), Lanczos et Réduction de base. Pour le solveur direct, on dispose des méthodes suivantes : Itération dans le sous-espace par blocs (BLSI), Lanczos et Réduction de base. Pour le solveur itératif, les méthodes suivantes sont disponibles : Lanczos modifiée (mode Pseudo - voir 3.5 et annexes 3A et 3B), gradient de Ritz (PCG_Ritz) et le gradient conjugué préconditionné (PCG).

Le solveur direct (SPDS) constitue l'une des variantes de l'élimination de Gauss. Ce solveur est vivement indiqué pour l'analyse de problèmes moyens à grands (de 10 000 à 200 000 équations) et constitue une alternative valable au solveur itératif.

3.1. Les Méthodes d'analyses modales

L'analyse modale se compose de deux approches de base. L'analyse de problème à valeurs propres

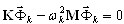k = 1,2,…,N (3.1)

est obtenue par la définition de valeurs propres wk et de vecteurs propres 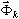. C'est la première approche bien connue des ingénieurs. La seconde approximation repose sur la génération des vecteurs de base

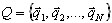(3.2)

et sur la recherche des approximations de Ritz , (k=1,2,..., N). Elle repose sur la méthode des vecteurs de Ritz, proposée par E.L. Wilson [1, 3] et appliquée à SAP2000. Cette approche s'applique pour l'analyse sismique et constitue une méthode puissante en cas de difficulté majeure à obtenir des pourcentages de masse suffisants (voir 3.5).

On utilise les méthodes Itération dans le sous-espace par blocs (BLSI), Itération sur sous-espace (SI), Lanczos à orthogonalisation sélective et Réduction de base (voir Annexe 3A) en cas de sélection de solveurs directs (Skyline ou SPDS). La méthode d'itération sur sous-espace est généralement lente. On recommande donc les méthodes BLSI ou Lanczos pour l'analyse de problèmes moyens et surtout très grands, si de très nombreuses valeurs propres sont concernées. La Réduction de base, utilisée par un ingénieur expérimenté, donnera de bons résultats. Elle requiert des informations supplémentaires sur les noeuds et les directions de base.

Gradient conjugué préconditionné (PCG)

Cette méthode est utilisée en première approche, si le solveur itératif a été retenu. Elle donne de bons résultats si très peu de modes propres sont extraites (jusqu'à 5). On l'utilise plus souvent pour l'analyse du vent que pour l'analyse sismique. On utilise la PCG pour l'estimation du mode propre le plus bas sur les systèmes importants.

Pour une présentation de la deuxième méthode (obtenue par analyse pseudo-mode), voir 3.5.

Itération en blocs (BLSI)

Cette méthode [1,3] est plus générale que la Méthode Lanczos, car elle accepte tous les types de matrices de masses (voir 3.2) et peut analyser des structures de façon individuelle. Les itérations dans un bloc de taille constante avec exclusion immédiate de vecteurs convergents et addition de nouveaux vecteurs initiaux permet d'accélérer les calculs par rapport à la méthode d'itération dans le sous-espace habituelle [1 à 3]. La méthode BLSI, comme la Lanczos, peut s'appliquer pour extraire un grand nombre de valeurs propres (jusqu'à 100 ou 200).

Itération dans le sous-espace (SI)

On peut utiliser cette méthode pour analyser tous les types de matrices de masse [4] ou de structures séparées. Cela dit, si de nombreux modes sont requis (plus de 10), cette méthode reste très lente, surtout appliquée à des systèmes très importants.

La puissance de la méthode Lanczos [12,16,17] permet d'obtenir un grand nombre de couples propres (de 20 à 500, voire plus). Bien qu'on l'appliquera de préférence à des systèmes importants, elle induit certaines restrictions :

• Il est impossible d'analyser des structures séparées.
• Les matrices de masses sont intégrées aux rotations ou de types homogènes
• Il est impossible d'ignorer la densité de la matière (il suffit alors d'affecter une faible densité fictive pour contourner ces limites).

Réduction de base

Cette méthode [5] est connue sous le nom de méthode évoluée de Rayleigh-Ritz [4] ou de Bubnov-Galerkin pour systèmes discrets. Cet algorithme permet d'obtenir des valeurs approximatives des premiers couples propres, si toutefois certains paramètres les concernant sont connus. La méthode demande la définition des degrés de liberté de type "maître" (MDOF - master degree of freedom) afin d’obtenir un système réduit. La procédure de création du modèle réduit peut donc être contrôlée. Il s'agit d'un outil puissant destiné aux ingénieurs expérimentés dans l'analyse dynamique de structures et habitués à certains types de structures au comportement connu. Cette méthode permet d'exclure les degrés de liberté (DOF) indésirables du modèle en réduction, et ramène le problème complexe initial (aux degrés de liberté nombreux) à une forme réduite. Ceci est possible avec beaucoup moins de degrés de liberté (DOF). L'expérience en matière d'analyse structurelle dynamique montre que les utilisateurs rencontrent certains problèmes quand les méthodes de réduction automatique (BLSI, SI et Lanczos) génèrent des calculs très complexes. Par exemple, les vibrations de barres isolées peuvent provoquer de sérieux problèmes, la recherche de couples propres se faisant automatiquement sans sélection préalable. Ceci s'applique à la majorité des cas de structures réelles. Dans le cas contraire, ces vibrations localisées seront contrariées par certaines contraintes non prises en compte dans l'analyse des éléments finis, ou leur participation sera insignifiante dans le déplacement global du système. En général, pour ces vibrations localisées, le pourcentage des masses participantes est très faible. Utiliser des méthodes exactes pour ce cas risque d'engendre les difficultés expliquées plus haut. La mise en oeuvre de la méthode approximative de réduction de base peut simplifier les calculs.

Gradient conjugué préconditionné (PCG)

Cette méthode [9-13] est disponible pour les solveurs itératifs. Cette méthode est recommandée pour l'extraction d'un petit nombre de couples propres sur des systèmes importants. Le Pseudo-mode (voir 3.5) et les méthodes Lanczos ou PCG_Ritz sont conseillés s'il faut déterminer un grand nombre de modes pendant l'exécution de l'analyse sismique ou spectracle et qu'un solveur itératif a été retenu.

Réduction de Ritz (PCG_Ritz)

Cette méthode [8] est disponible pour les solveurs itératifs en pseudo-mode. Elle permet d'obtenir une résolution approximative des termes des vecteurs de Ritz. Cette méthode permet des analyses sismiques et spectrales très rapide sur les systèmes de taille moyenne (de 10 000 à 100 000 équations).

Méthode de Lanczos modifiée

Cette méthode complète la méthode de Lanczos en cas d'application d'un solveur itératif. Son fonctionnement s'apparente à la méthode Lanczos en pseudo-mode. Différente de la méthode Lanczos pour solveurs directs, elle ne requiert aucune factorisation de matrice de rigidité. Ce sont alors les principes de la méthode de gradient préconditionné qui s'appliquent. De toutes les méthodes dynamiques associées aux solveurs itératifs, cette méthode est la plus fiable, bien qu'elle ne soit pas la plus rapide.

Les détails de toutes les méthodes dynamiques sont présentés dans l'annexe 3A.

3.2. Types de matrices des masses

Une structure peut recevoir des matrices simplifiées sans rotations, simplifiées avec rotations ou homogènes.

Les matrices simplifiées sans rotations et avec rotations sont les matrices de masses diagonales. Ces types de matrices de masses exigent très peu de calculs.

La matrice de masses homogènes s'affiche si le système étudié possède des paramètres répartis. Selon une idée très répandue, une matrice de masses homogène décrit plus fidèlement les propriétés d'inertie d'une structure qu'une matrice simplifiée. Or il s'avère que bien souvent, une matrice de masses simplifiée offre une approximation satisfaisante, les paramètres d'inertie étant évidemment établis avec moins de précision que les paramètres de rigidité. L'énergie cinétique est en fait intégrée aux déplacements structurels, tandis que l'énergie potentielle est exprimée par la dérivée spatiale des déplacements. On sait bien que l'erreur d'approximation augmente considérablement à chaque différenciation [4]. Pour les objets continus (solides, coques, dalles), il est donc possible d'établir une approximation des paramètres de masse moins précise que les paramètres de rigidité pour un même maillage.

Généralement, on retient les polynômes d'Hermite en tant que fonctions de forme des barres. Il s'agit d'une solution précise pour la plupart des problèmes statiques et des problèmes dynamiques, si la matrice des masses est de type simplifiée. Toutefois, des solutions exactes pour les problèmes dynamiques liés à une barre aux masses réparties appartiennent à la classe des fonctions de Krylov (combinaison spécifique de fonctions hyperboliques et trigonométriques). Elle permet de présenter les paramètres de rigidité en approximation quand les polynômes d'Hermite sont utilisés parallèlement à une matrice de masses homogènes. Elle n'a pas été conçue pour la mise en oeuvre d'un autre type de fonction de forme pour les problèmes statiques et dynamiques. Dans la plupart des cas, il n'est donc pas forcément avantageux de compliquer le modèle dynamique en faisant intervenir des paramètres de masse, la solution d'approximation avec des masses homogènes étant choisie à la place de la solution exacte pour un modèle approximatif (masses simples).

De plus, les masses d'éléments structurels (longerons, poteaux, etc.) sont généralement négligeables par rapport aux masses des voiles et des toit (charge permanente), qui sont prises en compte au moment de la conversion des charges permanentes en masses. Ces masses non structurelles réduisent généralement les effets de la répartition des masses des éléments.

Dans la plupart des cas pratiques, la matrice des masses simplifiée offre un degré d'approximation satisfaisant pour les propriétés d'inertie de la structure. Il convient de noter qu'une matrice de masses homogène requiert des calculs importants si l'analyse porte sur un problème de taille importante. Il faudra justifier de l'implémentation d'une matrice de masses homogènes avant de choisir un tel type de matrice en vue de l'analyse.

On part du principe que la matrice des masses est Homogène si les liaisons rigides font partie du modèle de calcul.

En cas d'application d'un solveur direct ou itératif, le calcul du produit matrice-vecteur s'effectue selon la technique "élément par élément" (EPE) est utilisée pour le calcul du produit matrice-vecteur. La matrice des masses homogènes ne pouvant pas être constituée, toutes les opérations se déroulent uniquement au niveau élémentaire. Dans le cas du solveur Skyline, une matrice des masses homogène est constituée et sauvegardée de la même façon qu'une matrice de rigidité. Pour les systèmes de petite taille (3 000 équations et moins), la technique Skyline est plus rapide, bien que sensiblement plus longue quand le système s'étoffe.

Il est possible d'utiliser des masses ajoutées et de convertir des charges statiques en masses.

Si les méthodes Lanczos, PCG_Ritz ou Lanczos modifiée (solveur itératif) sont sélectionnées, seules les matrices Simplifiée avec rotation et Homogène sont disponibles.

3.3. Limites hautes

Il est possible de calculer toutes les valeurs propres et les modes propres inférieurs à une valeur définie par l'utilisateur. Cette valeur est alors considérée comme la "limite haute". Quand cette option est activée, Robot recherche ω₁, ω₂, …, ω_n ≤ ω^*, où ω^* est la limite haute. L'algorithme fonctionne en deux étapes. La première comprend un contrôle de séquence selon Sturm, débouchant sur la définition du nombre de valeurs propres (n), par nature inférieure à la limite haute. La seconde voit la génération de n couples propres, chacun d'entre eux étant inférieur à la limite haute.

Les méthodes Lanczos et BLSI sont recommandées pour les types d'analyse utilisant les limites hautes, puisqu'il est nécessaire d'obtenir un nombre important de couples propres.

Le critère de masse participante (voir 3.4) est ignoré quand la limite haute intervient.

Par exemple, des problèmes peuvent survenir avec la norme sismique française PS-92, car elle impose que toutes les fréquences inférieures à 33 Hz soient prises en compte.

3.4. Masses participantes

Les masses participantes pour chaque mode (k=1,2,..., n) est défini comme

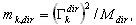
où , 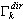est le coefficient de masse participante pour le mode propre K, I_dir est le vecteur de translation unitaire selon la direction (dir = X, Y, Z), est la masse totale selon la direction dir, 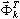est le k-ième mode propre, .

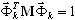Le pourcentage des masses participantes pour la direction dir est égale à M%dir 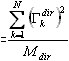. Il définit la contribution de tous les modes impliqués dans le mouvement d'une structure dans la direction étudiée.

Si vous avez choisi l'Analyse modale et que les masses participantes pour un nombre maximal de noeuds (défini) sont inférieures à la valeur requise, un message vous indique que le pourcentage de masses participantes ne convient pas, et ce sans incidence ni correction sur les calculs.

Il convient de choisir l'analyse sismique ou le pseudo-mode pour procéder à la recherche automatique du pourcentage de masses participantes requis. Pour des explications détaillées, voir 3.5.

3.5. Les modes d'analyse

Cette section présente les modes d'analyse suivants : Modale, Sismique et Pseudo-dynamique.

Certaines normes sismiques (UBC-97 ou la norme française PS-92) imposent que la somme des masses de chaque direction (ou seulement pour les directions horizontales) soit supérieure à 90 %. Des problèmes risquent de survenir au moment où la somme des masses requise est obtenue. Le résultat peut s'expliquer par un très grande nombre de faibles contributions provenant des modes les plus bas. Ceci s'explique généralement par le caractère local des modes les plus bas. Les modes Sismique et Pseudo-mode sont présentés pour tenter de régler de tels problèmes complexes. L'efficacité de ces approximations sera présentée dans l'Annexe 3C. La méthode Lanczos pour solveurs directs est disponible pour ces deux modes. Les méthodes Lanczos modifiée et PCG_Ritz sont disponibles pour le pseudo-mode quand le solveur itératif a été choisi.

Modale

Il s'agit d'une approximation bien connue qui figurait déjà dans les précédentes versions de Robot.

Les méthodes BLSI, SI, Lanczos et Réduction de base pour les solveurs directs et la méthode PCG pour solveur itératif sont disponibles.

Voici les critères de convergence des solveurs directs. L'itération s'arrête quand 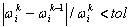, où i = 1, 2,..., N; k - étant le nombre d'itérations, N - le nombre de modes (choix de l'utilisateur). La méthode de réduction de base ne fait l'objet d'aucun contrôle de convergence. Bien que proche de la méthode de Ritz, il ne s'agit pas d'une approximation itérative. Il faut augmenter le nombre de degrés de liberté "maîtres" pour améliorer la précision des résultats.

Voici quelques critères de convergence pour la méthode PCG (solveur itératif) :

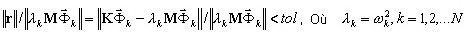
Voir Annexe 3A pour des explications détaillées.

La valeur Limites hautes est la valeur minimale de période, de fréquence et de pulsation. Si ce paramètre est différent de 0, tous les couples propres compris entre 0 et la limite haute seront calculés les uns après les autres.

Mass% est le pourcentage des masses participantes (somme des masses pour tous les modes calculés et pour chaque direction).

Le contrôle Sturm est une vérification des couples propres ignorés compris entre 0 et le paramètre de basculement . Il compte les éléments négatifs présents sur la diagonale de la matrice décomposée .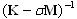

Cette procédure est très coûteuse sur les problèmes de grande taille. Notons que les analyses sismique et spectrale admettent des spectres de valeurs propres discontinus. La continuité du spectre ne sert qu'à valider un pourcentage des masses correct dans chaque direction. Si cette condition est remplie, l'intégrité de la base est garantie. L'implémentation de la méthode BLSI permet de procéder à la vérification partielle de la continuité du spectre des valeurs propres, sans qu'une vérification de Sturm soit nécessaire. Pour en savoir plus, voir la description de la méthode BLSI..

Nombre de modes	Limites hautes	% Masses	Comportement du programme
N	0 (inactif)	0 (inactif)	La vérification de Sturm est cochée. Les fréquences ignorées pour les N premiers modes sont manquantes. Le mode est disponible pour les solveurs directs quand les méthodes BLSI, SI ou Lanczos sont appliquées. Il n'est pas disponible pour la méthode de réduction de base et pour toutes les méthodes à solveurs itératifs. Définition des N premiers modes propres séquentiels. Exécution de la vérification de Sturm. Si des fréquences ignorées sont détectées, un message vous indique le nombre de fréquences ignorées. Plusieurs choix possibles : Oui - Le processus d'itération se poursuit, le nombre de couples propres ignorés est déterminé. Une nouvelle vérification de Sturm s'éxécute. Non - Les couples propres convergents sont enregistrés en tant que résultat final. Les calculs passent au cas suivant. Annuler - Les itérations se poursuivent. Toutes les fréquences ignorées sont établies. L'avertissement est ignoré. La vérification de Sturm n'est pas cochée. La vérification de Sturm n'est pas exécutée.
N	ω *	Inactif (car Limite haute active)	Le mode est disponible uniquement pour les solveurs directs et les méthodes BLSI, SI et Lanczos. Il n'est pas disponible pour la méthode de réduction de base et pour toutes les méthodes à solveurs itératifs. La vérification de Sturm est exécutée au début des calculs. On obtient le nombre de fréquences N1 compris entre zéro et la limite haute : 0 < ω1 < ω2 < … < ωN1 < ω* Si (N1 > N), vous recevez un message relatif au nombre de fréquences N1. Plusieurs choix possibles : Oui : Calcul de 0 < ω1 < ω2 < … < ωN1 < ω* Non : Fin des calculs. Si (N1 < = N) : Calcul de 0 < ω1 < ω2 < … < ωN1 < ω* sans le moindre avertissement. Dans les deux cas, il est possible de dériver un nombre de couples propres supérieur à N1, mais ceux-ci seront enregistrés sous forme de résultats seulement si : 0 < ω1 < ω2 < … < ωN1 < ω*. Tous les couples propres convergents supérieurs à ω* seront perdus.
N	Inactif (% Masses étant actif)	Actives : 0 < % Masses < = 100%	Disponibles pour toutes les méthodes de solveurs directs. Le mode n'est pas disponible pour le solveur itératif. Si la valeur % Masses n'est pas satisfaisante, l'utilisateur reçoit un message. Aucune correction n'est opérée. Dans le cas contraire, les calculs s'effectuent, similaires au premier cas.

Mode sismique

Ce mode est réservé aux solveurs Skyline ou directs.

En analyse sismique et spectrale, l'utilisation de couples propres en ordre séquentiel n'a aucune importance. En effet, seules les couples propres ayant un rôle considérable dans la réponse sismique doivent être pris en compte (leur coefficient de masse participante étant important). La vérification de Sturm n'est donc pas effectuée.

La méthode de Lanczos garantit généralement la convergence d'un nombre de couples propres très supérieur à N, dans l'ordre séquentiel croissant. Quand les valeurs propres ignorées doivent être rétablies, il est nécessaire que le nombre de fréquences convergentes soit très supérieur aux N premières fréquences souhaitées. Par exemple, bien souvent, la méthode Lanczos donne les fréquences convergentes suivantes.

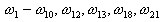
Quand l'utilisateur demande les couples propres en ordre séquentiel, il n'obtient que les 10 premiers. Les 4 derniers couples propres sont tout simplement "jetés", tout comme les contributions respectives des masses. Ce qui distingue le mode Sismique proposé, c'est qu'il prend en compte tous les couples propres convergents, et pas seulement les premiers. Il garantit des sommes des masses plus importantes que le mode Modal.

Méthodes d’analyse disponibles : Méthode Lanczos.

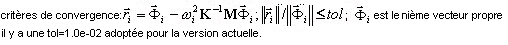
Les limites hautes sont ignorées.

Le calcul des masses participantes est la moyenne de M%x, M%y, M%z pour les systèmes 3D, et une valeur minimale de M%x, M%z pour les systèmes 2D (M%x, M%y, M%z représentent -respectivement- la somme des masses pour les directions x, y et z). Cette stratégie s'explique par le fait qu'il est souvent bien difficile de garantir un niveau de masses participantes suffisant pour la direction verticale. Vous pouvez vérifier le pourcentage de masses participantes pour chaque direction dans le résultat final.

Nombre de modes	Limites hautes	% Masses	Comportement du programme
N	Inactives	Inactives (0)	Calculer les N couples propres non-séquentiels. La vérification de Sturm n'est pas exécutée. Le nombre de couples propres convergents est égal à N.
N	Inactives	Actives : 0 < % Masses < = 100%	N est ignoré. Les calculs se poursuivent jusqu'à ce que le pourcentage de masses soit au moins égal au pourcentage souhaité, jusqu'à ce que le logiciel propose à l'utilisateur d'arrêter les calculs, ou jusqu'à ce que le nombre de couples propres convergents atteigne la valeur maximale possible. Cette valeur est définie en interne. Elle est fixée à 100 dans la version actuelle. Tous les 20 pas (Lanczos), le nombre de couples propres convergents et le pourcentage de masses participantes sont mis à jour. Un message vous indique le pourcentage de masses obtenu. Plusieurs choix possibles : Oui : Vous lancez le calcul de 20 pas Lanczos supplémentaires avant de revoir ce même message, si le pourcentage de masse n'est pas atteint (le nombre de couples propres convergents ne dépasse pas la valeur maximale possible). Non : Les couples propres convergents sont enregistrés comme résultats finaux et sont transmis au cas suivant. Annuler : Ignorer tous les prochains messages et poursuivre les calculs.

Pseudo-mode

Ce mode est disponible pour les solveurs directs et itératifs. Il est recommandé seulement en analyse sismique et spectrale quand les modes Modal et Sismique s'avèrent trop lents. Les modes Modal et Sismique utilisent des modes propres comme vecteurs de base pour présenter la réponse sismique. On peut requérir un très grande nombre de modes propres pour garantit une somme de masses suffisante pour certains systèmes délicats. Le pseudo-mode rejette cette idée et génère les approximations de Ritz correspondantes aux couples propres inférieurs, au moyen de vecteurs de Lanczos (pour les solveurs directs) ou de la Réduction de Ritz [8] et de la méthode de Lanczos modifiée pour les solveurs itératifs. Ce mode opératoire est plus efficace dans la plupart des cas, car le nombre de vecteurs de base nécessaires est moins important qu'en mode Modal. Ceci a été démontré par E.L.Wilson [1-3]. Le pseudo-mode est identique aux vecteurs de Ritz proposés en [1 à 3] et appliqués dans SAP2000. Précisons que la norme française PS-92 admet l'application d'approximations de caractère scientifique pour l'addition de systèmes de vecteurs de base aux modes propres existants, ce afin d'augmenter la somme des masses. Pour une présentation détaillée du pseudo-mode et de son efficacité, voir les Annexes 3B et 3C.

Les limites hautes sont ignorées.

Le calcul des masses participantes est définie comme la moyenne de M%x, M%y, M%z pour les systèmes 3D, et comme valeur minimale de M%x, M%z pour les systèmes 2D (M%x, M%y, M%z représentent -respectivement- la somme des masses les directions x, y et z). Cette stratégie s'explique par le fait qu'il est souvent bien difficile de garantir un niveau de masses participantes suffisant pour la direction verticale. Vous pouvez vérifier le pourcentage de masses participantes pour chaque direction dans le résultat final.

Nombre de modes	Limites hautes	% Masses	Comportement du programme
N	Inactives	Inactives (0)	Disponible pour les solveurs directs et itératifs. Génère N vecteurs de base pour définir le sous-espace de travail. Enregistre N vecteurs de base pour utilisation en analyse sismique et spectrale. Ce choix est particulièrement indiqué.
N	Inactives	Actives : 0 < % Masses < = 100%	Disponible uniquement pour les solveurs directs Génère N vecteurs de base pour définir le sous-espace de travail. Enregistre ces vecteurs de base, suffisants pour obtenir le pourcentage de masses indiqué. Le nombre de vecteurs de base enregistrés est inférieur à N, si % Masses < 100 %

3.6. Analyse spectrale

On applique la méthode Spectre de réponse en analyse sismique et spectrale. Elle consiste à décomposer une structure de plusieurs degrés de liberté (MDOF) pour en faire un système d'oscillateurs à un seul degré de liberté (SDOF). La réponse pour chacun de ces oscillateurs et la sommation statistique des réponses extrêmes pour chaque oscillateur se calculent au moyen des méthodes SRSS, CQC, 10 % et de la double somme [3, 21].

Ce système d'oscillateurs SDOF est défini par les modes propres (en mode Sismique ou Modal). Ce système d'oscillateurs SDOF est défini par les vecteurs de base de pseudo-mode (en Pseudo-mode, voir 3.5).

L'introduction du pseudo-mode requiert une nouvelle approximation de l'évaluation de la réponse pour chaque mode. Voici l'approximation classique :

( 3.1.1 )

où K, M - rigidité et matrices des masses, Γ - coefficient de masse participante, S_a - accélération spectrale, T - période, i - nombre de mode, k - échelle du spectre, dir - indice de direction du mouvement sismique (dir = X, Y, Z), x - vecteur de déplacement pour la réaction maximale du mode-i.

Posons maintenant ceci (voir Annexe B) :

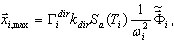( 3.1.2 )

où indique un vecteur de base (il n'est pas nécessaire que soit une approximation exacte de - le vecteur propre exact de ω_i - l'approximation de la valeur propre exacte Ωi. Il est possible de démontrer que (3.1.1) propose la même solution que (3.1.2), si (ωi = Ωi). Toutefois, (3.1.2) ne s'applique pas seulement pour les solveurs directs, mais aussi pour les solveurs itératifs. La procédure de résolution correspondant à la matrice de rigidité (K) n'est pas obligatoire. Cette méthode est plus rapide que (3.1.1) et offre plus de sûreté dans le contrôle des résultats (somme des forces - somme des réactions).

La formule ci-dessous découle de (3.1.1)

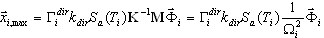( 3.1.3 )

Le vecteur de réponse modale décrit la réponse extrême de la correspondance de l'oscillateur SDOF. Il faut consacrer l'étape suivante à la définition de la réponse finale de la structure MDOF au moyen de moyennes statistiques entre les modes et entre les directions sismiques.

Les précédentes versions de Robot permettent d'affecter plusieurs directions sismiques statistiquement indépendantes, avec leurs propres coefficients d'homothétie dans un cas de charge. On obtient la moyenne statistique des directions par le calcul de la somme des valeurs absolues et de la racine carrée de la somme des combinaisons carrés à l'intérieur de chaque mode. Les options correspondantes figurent dans Préférences du projet.

L'option "Somme des valeurs absolues" propose :

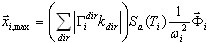( 3.1.4 )

L'option "Racine carrée de la somme des carrés" calcule la moyenne du des directions sismiques comme .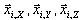

( 3.1.5 )

Il est possible de montrer que chaque composant de est la combinaison SRSS des composants correspondants de ,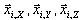

où i =1,2,...,N indique le numéro du mode ou du pseudo-mode.

On applique la combinaison CQC ou SRSS entre les modes (ou pseudo-modes) pour obtenir la réponse finale de la structure MDOF étudiée, après obtention des vecteurs de réponse modale moyens , où i =1,2,..., N.

Les vecteurs de réponse modale moyens , où i =1,2,...,N sont les mêmes pour "Somme des valeurs absolues" et pour "Racine carré de la somme des carrés", si la direction sismique individuelle a été définie pour le cas de charge étudié (par exemple, Kx=Kz=0, Ky=1).

A partir de la version 12.2, Robot enregistre la procédure de calcul de la moyenne entre les directions sismiques, bien qu'il permette dans l'absolu d'exécuter l'approximation la plus efficace. Il est recommandé de définir une seule direction sismique pour chaque cas de charge, puis d'appliquer soit la combinaison SRSS entre les directions (conformément à la norme américaine) ou les combinaisons dites de "Newmark" (conformément à la norme sismique française PS-92 et à la norme Eurocode-8).

Étudions maintenant les nouvelles possibilités à l'aide d'un exemple typique.

Dans cet exemple (un mouvement sismique simple par cas de charge), on a, pour les valeurs typiques des coefficients d'homothétie :

Kx=1; Ky=Kz=0 pour dir = X (cas de charge S_X)

Kx=0; Ky=1; Kz=0 pour dir = Y (cas de charge S_Y)

Kx=Ky=0; Kz=0.7 pour dir = Z (cas de charge S_Z - on pose une intensité de mouvement vertical équivalente à 2/3 de l'intensité du mouvement horizontal)

Trois cas de charges sont définis pour chaque mouvement sismique statistiquement indépendant. La réponse modale pour chaque cas sera identique à (3.1.2) (I = 1,2,..., n; dir = X, Y, Z).

Il faut ensuite définir le facteur moyen de tous les modes, pour chaque sens de mouvement sismique :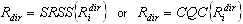

où 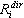- est l'un des facteurs (déplacement, force, contrainte, etc...), pour le i-ème mode dû au mouvement sismique dans la direction dir, qui correspond à la réponse modale (obtenues à partir de (3.1.2)).

Rdir est le résultat de la combinaison SRSS ou CQC sur tous les modes (pseudo-modes) étudiés

On procède ensuite à la moyenne des sens sismiques actifs, selon l'option choisie.

Soit par combinaison SRSS :

Les options d'analyse spectrale admettent la définition d'un spectre arbitraire de sens sismique.

3.7. Analyse sismique

On applique la méthode Spectre de réponse en analyse sismique et spectrale. L'analyse sismique est exécutée sur la base de l'analyse spectrale (voir 3.6). Cependant, les accélérations spectrales Sa = Sa(Ti) sont générées pour correspondre à une norme sismique sélectionnée, au lieu d'être affectées par l'utilisateur (comme c'est le cas pour l'analyse spectrale).

La norme sismique UBC-97 est disponible dans Robot à partir de la version 12.0. L'analyse Spectre de réponse s'effectue conformément aux sections 1631.5.1 - 1631.5.3 de l'Uniform Buidling Code de 1997. Il est possible de respecter les dispositions de la section 1631.5.4 ("Elastic Response Parameters may be reduced …") au moyen des mécanismes combinatoires de Robot. Les termes de cisaillement Vx, Vy, Vz, les termes de moment de renversement Mx, My et Mz, le moment de torsion Mz (on suppose que l'axe OZ est vertical) figurent tous dans le tableau "Réactions" à la ligne "somme des forces", pour chaque réponse modale et pour les combinaisons SRSS et CQC entre les modes.

Les normes sismiques suivantes sont disponibles dans le programme :

• UBC97
• PS 69 R. 82
• AFPS
• PS 92
• RPA 88
• DM 16.1.96
• EC 8
• IBC 2000
• P100-92
• Norme turque
• Normes chinoises
• Norme argentine
• EAK 2000.

3.8. Filtres de sélection

Seuls les modes dotés d'un coefficient de masse participante relativement élevé contribuent de façon significative à la réponse sismique d'une structure. Il suffit donc de prendre en compte uniquement ces modes. Les autres modes, dotés d'un coefficient de masse participante peu élevé, peuvent être ignorés pendant l'analyse sismique. Le nombre de modes dérivée est souvent beaucoup plus élevé que le nombre obtenu par évaluation des masses participantes. Si seuls les modes dotés de coefficients de masse participante élevés sont retenus, il est possible d'économiser de l'espace sur le disque et du temps de calcul.

On peut utiliser deux méthodes (au choix).

• Créer une liste de modes acceptés pour chaque sens sismique (cas sismique) sur la base de résultats obtenus précédemment dans l'analyse modale
• Affecter une masse limite pour le pourcentage des masses - modal - (tous les modes dont le pourcentage de masses participantes est inférieur à cette limite ne seront pas pris en compte).

La première méthode est la plus efficace, bien qu'elle nécessite une analyse modale préalable. La seconde méthode permet d'appliquer des filtres en analyse spectrale et sismique. Attention, elle occupe plus d'espace sur le disque et sollicite davantage les ressources de l'ordinateur.

Voici un autre exemple. Voici, ci-dessous, les résultats de l'analyse modale, dans le tableau 3.1, dans lequel les cas sismiques sont définis comme suit : Dir_X (Kx=1; Ky=Kz=0), Dir_Y (Kx=0; Ky=1; Kz=0) et Dir_Z (Kx=Ky=0; Kz=1)

Tableau 1

N° mode	Masse particip. UX (%)	Masse particip. UY (%)	Masse particip. UZ (%)	Période
1	0.05	12.01	0.004	0.803
2	67.43	0.06	0.005	0.705
3	0.002	0.08	0.07	0.686
4	0.001	0.008	0.009	0.650
5	25.4	0.07	2.06	0.590
6	0.09	68.5	5.05	0.540
7	0.08	10.3	0.06	0.490
8	0.07	0.06	0.56	0.460
9	0.05	0.07	30.56	0.420
10	0.08	0.06	0.25	0.380
11	0.06	0.01	26.7	0.270

Supposons que nous prenions en compte tous les modes ayant un coefficient de masse participante supérieur à 1 %. Les valeurs de masse participante correspondantes sont données dans le tableau. On remarque que si les sens sismiques sont affectés en tant que (1 0 0) pour le cas Seism_X, les modes au coefficient de masse participante important pour les directions UY, UZ ne participent pas du tout à la réponse sismique (voir 3.6) :

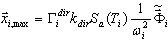
où dir = X, Y, Z - sens du mouvement sismique ; -réponse maximale pour le mode-i ; 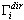- coefficient de masse participante ; Sa(Ti) - accélération spectrale ; - vecteur propre i ou vecteur de base (si pseudo-mode). Le multiplicateur scalaire sur le côté droit de la formule ci-dessous définit la contribution du mode-i dans la réponse sismique de la direction dir. Dans ce cas, où Ky = Kz = 0, la contribution des modes 2 et 5 est considérable. Les autres modes ne participent pas à la réponse sismique. Ceci s'explique par le multiplicateur Kdir (dir = Y, Z), égal à 0, et aux faibles valeurs de masse participante pour la direction dir=X. On peut montrer (de la même manière), que pour le cas Dir_Y, il suffit de prendre en compte les modes 1, 6 et 7, et les modes 5, 6, 9 et 11 pour Dir_Z.

Ainsi, en appliquant des filtres, le programme risque de ne prendre en compte que les modes appropriés - 2 pour Dir_X, 3 pour Dir_Y et 4 pour Dir_Z. Ceci se produit sans diminution notable des contributions des masses. Il convient de remarquer que sans les filtres, il faudrait appliquer les 11 pour chaque cas.

Cette approche permet de réduire le temps de calcul pour les problèmes dynamique de grande taille (ainsi que l'espace disque utilisé et la quantité de données à traiter), sans réduction notable de la précision du résultat par rapport à la méthode traditionnelle (quand les filtres de sélection ne sont pas utilisés).

Par exemple, le problème de grande taille PJG203 contient 34 266 équations (bande passante de 990 après optimisation). Le modèle d'éléments finis correspondant est présenté dans l'Annexe 3D - voir Fig. A1. Le calcul des 25 couples propres et de la matrice des masses homogène n'était pas encore effectué. Le temps de calcul est d'environ 50 heures sur un Pentium PRO (64 Mo de RAM, 200 MHz). L'espace disque requis dépasse 1 Go. Sans oublier un problème survenu au niveau du module de dimensionnement des aciers, provoqué par l'insuffisance de l'espace disque. (le calcul des combinaisons SRSS et CQC imposait le stockage des données de 25 modes, à multiplier par 3 cas sismiques comprenant de multiples degrés de liberté pour tous les facteurs - déplacements, forces internes, contraintes). L'application de filtres sélectifs permet au programme de résoudre ce problème.

3.9. Analyse harmonique

Soit la définition suivante de réaction constante d'une structure à l'action d'une charge simple / harmonique :

F(t) = F sin( ωt)

où w est la pulsation de la charge d'excitation. Soit le comportement d'une structure tel que :

(K - ω² M) X = F,

où X est l'amplitude du vecteur de déplacement.

3.10. Analyse temporelle

La méthode de décomposition modale (superposition) est prise en charge par Robot. Elle repose sur la représentation d'un mouvement de structure en tant que superposition du mouvement de modes non conjuguées. La méthode demande donc de déterminer les valeurs et les vecteurs propres. La méthode Lanczos est recommandée dans ce contexte. La méthode de décomposition modale utilise les équations réduites non conjuguées. Cette méthode est indiquée pour analyser la réponse dynamique de structures soumises à des charges dynamiques prolongées (par exemple, les charges non constantes provoquées par des engins de chantier ou des mouvemens sismiques). Pour des précisions mathématiques et les particularités de l'application, voir [3,4,6].

L'analyse temporelle (sans amortissement) peut être exprimée par la formule suivante :

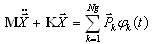(3.11.1)

où Ng - Nombre de "groupes de charges", φ_k(t) - données temporelles du k-ième groupe de charges.

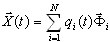(3.11.2)

où 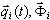- i-ème coordonnée normale correspondante et mode (vecteur propre ou vecteur Ritz). Le remplacement de (3.11.2) par (3.11.1) et l'ajout de termes d'amortissement entraîne les équations modales non-conjuguées suivantes [3,4,6] :

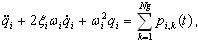(3.11.3)

où 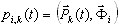, ξi - paramètre modal d'amortissement (généralement ξi = de 0,05 à 0,2 ; une valeur ξi = 1 indique un amortissement critique ; limite entre mouvement d'oscillation et mouvement apériodique), ωi - fréquence de vibration naturelle (pulsation), i=1,2,..., N

Chaque équation fait l'objet d'une résolution numérique. On applique la méthode de second ordre avec sélection automatique de l'étape d'intégration. Le vecteur de déplacement obtenu aux points temporels définis t = t1, t2, …, t5 est obtenu par substitution de qi (t5) dans (3.11.2).

La méthode de décomposition modale peut s'appliquer pour l'analyse de la réponse sismique. L'équation de mouvement devient alors,

(et les équations modales résultantes non conjuguées) :

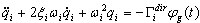(3.11.5)

où 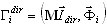est le coefficient de masse participante pour le i-ème mode et le sens du mouvement sismique dir. Chaque mode doit être normalisé comme suit : 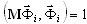. Enfin, tous les résultats (déplacements, vitesses, accélérations, forces internes, réactions, etc.) sont enregistrés uniquement pour les points temporels définis t = t1, t2, …, t5. Les performances du post-processeur permettent d'analyser les résultats de l'analyse temporelle dans des diagrammes ou dans des tableaux. Le mode diagramme affiche les facteurs sélectionnés (déplacement, accélération, vitesse, réactions, efforts tranchants, moments de flexion et autres) pour les degrés de liberté (DOF) choisis et présente la déformation de la structure au point temporel sélectionné. Le mode tableau permet non seulement de voir les correspondances de valeurs, mais aussi de rechercher automatiquement les valeurs maximale et minimale dans les facteurs de réponse sur tous les points temporels stockés.

3.11. Analyse modale tenant compte des forces statiques

On tient compte des petites vibrations linéaires par rapport à l'état d'équilibre statique induit par une charge statique donnée. Les forces statiques sont réputées pour leur influence sur les fréquences de vibrations naturelles. Normalement, l'analyse modale ne tient pas compte de cette influence. Mais la prise en compte des forces statiques dans l'analyse modale est bien possible.

Des équations complètes non-linéaires décrivent le mouvement de l'état d'équilibre relativement statique d'un système, induit par les charges statiques données.

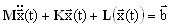(3.12.1)

où M, K - les matrices de masse et de rigidité, L(x(t)) - opérateur non-linéaire, x(t), b - vecteur de déplacement et vecteur de charge. La procédure de linéarisation se déroule comme suit :

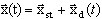(3.12.2)

où x_st est une partie de la solution commune décrivant l'état d'équilibre statique et x_d (t) est un vecteur de petits déplacements dynamiques. On peut assimiler l'opérateur non-linéaire à une décomposition de Taylor

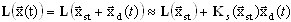(3.12.3)

où 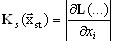est la matrice de contrainte-rigidité, une matrice jacobienne tenant compte de l'action des forces statiques. On a donc :

La première expression est issu de la linéarisation de petits déplacements dynamiques (remarque : 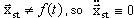). La seconde décrit l'état d'équilibre statique non-linéaire. On peut donc présenter un léger mouvement dynamique par rapport à l'état d'équilibre statique comme suit :

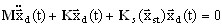(3.12.5)

Remplaçons x_d (t) = Φ e^{i ω t}. (3.12.5) provoque un problème de valeur propre

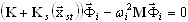(3.12.6)

où ω_i - valeur propre; Φ_i - vecteur propre.

Les calculs se font en deux étapes :

1. Analyse linéaire (3.12.7) ou non-linéaire (3.12.8) de l'état contraint statique provoqué par une charge statique déterminée

   K x_st = b (3.12.7)

   K x_st + L(x_st ) = b, (3.11.8)

   où x_st - vecteur inconnu d'état statique, b - vecteur de forces statiques déterminées (vecteur de charge statique), K - matrice de rigidité, L (x_st, b) - opérateur non-linéaire. Le vecteur de charge statique b peut résulter de la combinaison de plusieurs charges statiques. Notons ici que l'approche linéaire ne respecte pas complètement l'équation d'équilibre non-linéaire (3.11.8). Le vecteur x_st de l'état d'équilibre statique est donc le résultat d'une solution approximative, et la matrice contrainte-rigidité K_s(x_st) contient une erreur. Si la structure étudiée est suffisamment rigide et qu'elle laisse apparaître des effets non-linéaires faibles, cette approximation semble alors correcte. Dans le cas contraire, il est nécessaire de résoudre le problème statique non-linéaire (3.11.8) (cette technique ne figure pas dans le manuel). Naturellement, l'approche linéaire (3.2.17) est plus rapide que la non-linéaire (3.11.8). Pour l'approche linéaire, on a : K_s(x_st ) = G (x_st )= G, où G est une matrice de rigidité géométrique.

2. Analyse de valeurs propres (3.12.6)

   On sait que les valeurs positives de ωi (ωi > 0) représentent les états d'équilibre stable, et les valeurs négatives (ωi < 0), les états d'équilibre instable. Une valeur égale à zéro (ωi =0) correspond à l'absence de stabilité (flambement).

   La perte du caractère définitif de la matrice K + K_s(x_st) signifie que la charge statique dépasse sa valeur critique (flambement). Un message s'affiche alors. La convergence sera perdue pendant l'exécution du problème statique non-linéaire (3.11.8). Il est conseillé d'interrompre les calculs tant qu'on doute de leur pertinence.

   Seule l'approche non-linéaire est disponible pour les structures contenant un câble et des éléments en tension-compression.

Voyons l'exemple de la figure suivante.

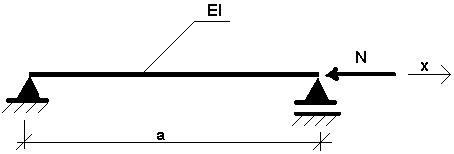
Fig. 3.11.1

Soit N - charge statique. L'expression suivante décrit le comportement d'un tel système :

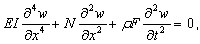( 3.11.9 )

où : w - déplacement de courbure, ρ - densité du matériau, F - aire de section transversale.

On détermine la solution comme suit :

( 3.11.10 )

Après remplacement de (3.11.10) par (3.11.9), on obtient :

, ( 3.11.11 )

où 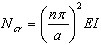- charge de flambement, ω₀ - valeur propre pour N = 0 (résultat de l'analyse modale classique). Enfin,

( 3.11.12 )

où ω - valeur propre pour le système soumis à une charge statique N. Ce résultat est visible en Fig. 3.11.2:

Fig. 3.11.2

La dépendance ω = ω (λ), où l est un paramètre de charge, pour une structure réelle apparaît souvent plus complexe que sous la forme (3.11.12) (voir [1,22]).

Annexe 3A

Méthodes de résolution de valeurs propres

Il convient d'avoir à l'esprit que la méthode universelle de résolution d'un problème propre n'existe pas.

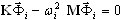, i=1,2,…,n ( A1 )

où K est la matrice de rigidité, M la matrice des masses, le mode propre et ω_i la pulsation. Pour la plupart des problèmes, une telle méthode est moins gourmande que d'autres en ressources (temps de calcul, stockage sur le disque dur). Cela dit, elle tient compte des différentes situations si d'autres tâches sont exécutées. Le choix d'une autre méthode est donc recommandé. La présente version de Robot couvre plusieurs méthodes de résolution de problème de valeurs propres généralisé (A1). Chacune a ses avantages et ses inconvénients. Voici, ci-dessous, quelques recommandations pour choisir la bonne méthode d'analyse. Nous espérons que, dans la majorité des cas, elles vous donneront les résultats escomptés.

La méthode d'Itération sur sous-espace (SI) étant expliquée dans [4], elle ne sera donc pas décrite ici.

Lanczos

La méthode Lanczos [12,16,17] est une approche puissante et fiable utilisée pour la résolution de problèmes de valeurs propres importants (A1). Elle est disponible quand les solveurs Skyline ou directs sont sélectionnés.

Cette approche trouve les N premières valeurs et premiers modes propres requis avec un maximum de précision. Plus on obtient de couples propres requis, plus la méthode Lanczos est avantageuse. L'approche implique toutefois quelques limites.

La matrice tri-diagonale T ne doit pas être décomposée. Il est impossible d'analyser une structure contenant plus de deux sous-structures non reliées. Pour ce genre de cas, chaque sous-structure est à étudier séparément, ou il faut faire appel à une autre approche (par exemple, une itération BLSI ou les méthodes de réduction de base).

La matrice des masses M sera Simplifiée avec rotations ou Homogène.

Une densité ne peut être nulle.

La méthode Lanczos utilise la réduction en matrice à trois diagonales T

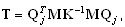, ( A2 )

où Q_j = {q1, q2, … , qj} est la matrice rectangulaire Neq x j, Neq est le nombre d’équations, j est le nombre de "pas" de Lanczos, et qj le j-ème vecteur de Lanczos. L'expression

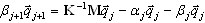( A3 )

génère le vecteur Lanczos suivant (qj + 1) et définit la ligne courante de la matrice T.

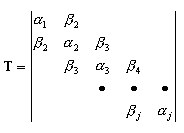
On obtient alors le problème de valeurs propres suivant :

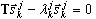, k=1,2,…,j ( A4 )

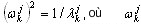est la j-ème approximation vers ω_k, k=1,2,…,n, n étant le nombre de couples propres requis. L'algorithme poursuit les calculs (pour augmenter j, le nombre de pas de Lanczos), jusqu'à ce que la précision souhaitée soit obtenue pour toutes les valeurs propres requises.

La procédure d'orthogonalisation sélective prend en charge le niveau d'orthogonalité requis entre les vecteurs Lanczos qj, ce qui garantit la fiabilité et la stabilité numérique des calculs. Nous emploierons des méthodes économiques pour fournir une orthogonalisation sélective et réduire le problème de valeurs propres réduit (A4) par des itérations QR doubles avec inversions.

Les vecteurs propres sources sont déterminés par la formule suivante

( A5 )

Les détails sont présentées dans [12,16,17].

Méthode de réduction de la base

Cette méthode [4, 5] est connue sous le nom de méthode de Rayleigh-Ritz améliorée [4]. Pour une telle méthode, on introduit une variante : la méthode de Bubnov-Galerkin. Cet algorithme permet d'obtenir des valeurs approximatives des premiers couples propres, si toutefois certains paramètres les concernant sont connus. La méthode demande la définition des degrés de liberté de type "maître" (MDOF - master degree of freedom) afin d’obtenir un système réduit. La procédure de création du modèle réduit peut donc être contrôlée. Il s'agit d'un outil puissant destiné aux ingénieurs expérimentés dans l'analyse dynamique de structures et habitués à certains types de structures au comportement connu. Cette méthode permet d'exclure les degrés de liberté (DOF) indésirables du modèle en réduction, et ramène le problème complexe initial (aux degrés de liberté nombreux) à une forme réduite. Ceci est possible avec beaucoup moins de degrés de liberté (DOF). L'expérience en matière d'analyse structurelle dynamique montre que les utilisateurs rencontrent certains problèmes quand les méthodes de réduction automatique (BLSI, SI et Lanczos) génèrent des calculs très complexes. Par exemple, les vibrations de barres isolées peuvent provoquer de sérieux problèmes, la recherche de couples propres se faisant automatiquement sans sélection préalable. Ceci s'applique à la majorité des cas de structures réelles. Dans le cas contraire, ces vibrations localisées seront contrariées par certaines contraintes non prises en compte dans l'analyse des éléments finis, ou leur participation sera insignifiante dans le déplacement global du système. En général, pour ces vibrations localisées, le pourcentage des masses participantes est très faible. Utiliser des méthodes exactes pour ce cas risque d'engendre les difficultés expliquées plus haut. La mise en oeuvre de la méthode approximative de réduction de base peut simplifier les calculs.

Cette méthode présente toutefois quelques inconvénients.

L'utilisateur doit affecter les MDOF : les noeuds "maîtres" et les directions principales. On admet que seuls les déplacements peuvent être pris comme degrés de liberté de type "maître" (ceci ne s'applique pas aux rotations).

L'algorithme s'applique à tout type de matrice des masses. On estime toutefois que le type de matrice des masses Simplifiée sans rotations est le plus bénéfique en termes de temps de calcul.

• La case Vérification de Sturm n'est pas disponible. Il n'existe qu'une seule façon de vérifier la convergence. Augmentez le nombre de MDOF (affectez d'autres noeuds "maîtres" et d'autres directions principales), procédez à une nouvelle résolution du problème, puis comparez les valeurs propres.

Une telle méthode transforme le problème source de valeurs propres pour modèle d'éléments finis

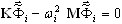(A6)

(A1) en problème de valeurs propres pour modèle en réduction

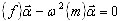(A7)

où {f} est la matrice d'influence, {m} est la matrice des masses générale pour un modèle en réduction,

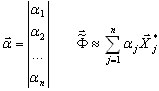(A8)

où n est le nombre de degrés de liberté d'un modèle en réduction. La base de telles transformations est une solution statique obtenue pour les états unitaires étudiés. Les forces nodales unitaires s'appliquent donc à chaque noeud "maître", dans la direction principale sélectionnée. Un problème statique de grande échelle est résolu pour n côtés droits :

i = 1, 2, …, n (A9)

où Ti est le vecteur de charge correspondant à i, la charge unitaire. L'utilisateur doit affecter les noeuds "maîtres" et les directions principales. Toutes les opérations demandées seront réalisées par le programme.

On résout le problème réduit de valeurs propres par la méthode de Jacobi, ce qui donne les fréquences approximatives ω_i, les modes , i=1,2,..., n. Cette approche est présentée en détail dans la partie [5].

Méthode d'itération dans le sous-espace par blocs

La méthode BLSI (itération dans le sous-espace par blocs) permet de résoudre un problème généralisé de valeurs propres (A1). Elle est disponible pour les solveurs Skyline et directs. Cette méthode est puissante et fiable. Elle est fortement conseillé en cas d'apparition d'un système à grande échelle, et quand il est nécessaire d'obtenir un grand nombre de couples propres (plus de 10). La méthode BLSI s'applique pour analyser des structures séparées. Tous les types de matrices des masses sont disponibles pendant l'analyse modale (Simplifiée sans rotations, Simplifiée avec rotations et Homogène). L'aire d'application de cette approche est limitée par le mode modal. Le mode Sismique et le Pseudo-mode restent disponibles si la méthode Lanczos a été choisie.

Le contrôle séquentiel de Sturm est opéré pour détecter les valeurs propres ignorées. BLSI contrôle la continuité des valeurs propres convergentes. Des valeurs propres convergentes discontinues indiquent la présence de valeurs propres ignorées. La continuité des valeurs propres convergentes ne signifie pas pour autant qu'il manque des valeurs propres. Les résultats des nombreux calculs indiquent toutefois que dans la plupart des cas, les vérifications de Sturm ne détectent pas les valeurs propres ignorées, alors que la méthode BLSI assure la continuité de la convergence. L'avantage de cette méthode est d'éviter la fastidieuse vérification de Sturm quand il n'est pas nécessaire de s'assurer de la présence des valeurs propres ignorées. Dès qu'une discontinuité de valeurs propres convergentes est détectée, le message suivant s'affiche (voir Fig. A1).

Le principal objectif de la méthode BLSI [1-3] est de réaliser plusieurs itérations vectorielles simultanées dans le sous-espace étudié. Chaque vecteur convergent est supprimé du sous-espace de travail (bloc) et remplacé par un nouveau vecteur initial. L'orthogonalité des vecteurs convergents est vérifiée à chaque pas d'itération.

On conseille l'application de la procédure d'accélération du décalage [1,4] pendant l'analyse modale si la convergence s'avère trop lente.

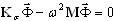, ( A10 )

où K_σ= K - σ M, σ - valeur de décalage. En début d'analyse, on pose σ = 0. La valeur de décalage est mise à jour automatiquement, si de nouvelles valeurs propres convergentes n'apparaissent pas du fait du nombre de pas d'itération. Prenons par exemple un nombre de pas de contrôle égal à 5. Après 4 itérations, 5 valeurs propres convergentes apparaissent. La valeur de décalage est toujours σ = 0. Au prochain pas d'itération, 3 valeurs propres convergent. La valeur de décalage est toujours σ = 0. Ensuite, au cours des 5 pas d'itération, aucune convergence de modes propres ne se réalise. L'algorithme détecte à nouveau la "convergence lente", pose σ = ω₈ ², met à jour K_σ = K - σ M et factorise la matrice décalée actualisée K_σ. Puis, après 2 pas d'itération, 2 modes propres convergent. La valeur de décalage reste ω₈ ². Puis, pendant les 5 pas d'itération suivants, aucune convergence de valeurs propres ne survient. L'algorithme détecte à nouveau la "convergence lente", pose ω₁₀ ² , met à jour K_σ = K - σ M et factorise la matrice décalée actualisée K_σ.

Fig. A1 La discontinuité de valeurs propres convergentes est détectée pendant l'exécution de la méthode BLSI.

Plusieurs choix possibles :

• Oui : Les calculs se poursuivent jusqu'à la prochaine valeur propre convergente. La vérification suivante est alors réalisée.
• Non : Les résultats sont enregistrés et les calculs passent au cas suivant.
• Annuler : Les calculs se poursuivent aussi longtemps que la continuité totale des valeurs propres convergentes est vérifiée. Le message est alors ignoré.

Ceci ne constitue pas l'ensemble des recommandations. Vous pouvez décider d'appliquer ou de ne pas appliquer les accélérations de décalage. Attention : l'application du décalage approprié est un puissant outil d'accélération de la convergence. Dans le cas contraire, chaque factorisation de la matrice actualisée K_σ peut s'avérer fastidieuse, surtout pour les systèmes à grande échelle. La décision finale en matière d'application du décalage repose sur l'expérience et l'intuition de l'utilisateur.

L'exemple qui suit illustre les avantages de l'application du décalage. Le modèle de calcul est indiqué en Fig. A2. On a 50 modes propres extraits par la méthode BLSI. Le solveur Skyline est sélectionné. Une tolérance de 1,0e-09 est retenue. On voit que la convergence à partir du mode 38 est si lente qu'aucun résultat n'a encore été obtenu au bout de 20 minutes de calculs. Après activation de l'accélération du décalage (l'actualisation du décalage a été accepté pour chacun des 5 pas d'itération - avant conversion) le temps de calcul est encore de 50 secondes. On pourrait ainsi multiplier les exemples de réduction du nombre d'itérations du fait de l'application du décalage, mais il faut retenir que ceci allonge les calculs. Nous recommandons d'activer l'accélération des décalages quand, les décalages étant désactivés, une approche classique provoque un grand nombre d'itérations pendant l'application de la méthode BLSI.

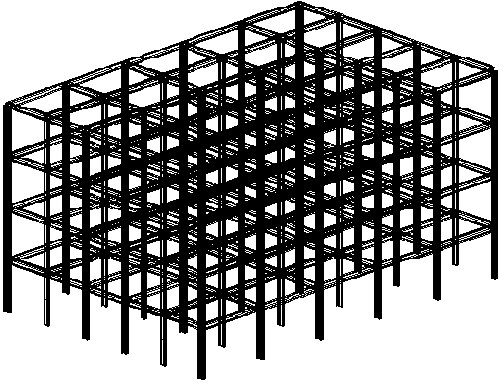
Fig.A2 Ossature spatiale

Méthode de Lanczos modifiée

Il s'agit d'une variante de la méthode Lanczos en pseudo-mode, à l'usage des solveurs itératifs. La méthode Lanczos classique impose la factorisation de la matrice de rigidité (voir A3). En présence d'un système à grande échelle, la factorisation de la matrice de rigidité reste très longue. Pour les systèmes importants (plus de 100 000 équations), la factorisation de la matrice de rigidité réclame non seulement beaucoup de calculs, mais la solution d'un système d'équations de matrices correctement factorisées s'avère également très coûteuse.

La méthode de Lanczos modifiée repose sur l'approche itérative. Elle évite le stockage, l'assemblage et la factorisation d'une matrice de rigidité très étendue. L'évaluation d'un seul vecteur de Lanczos nécessite à peu près autant de calculs que la résolution d'un problème statique comprenant un seul côté droit. Quant au pseudo-mode, la méthode réduit le nombre de vecteurs de Lanczos par rapport au mode Modal appliqué en cas d'exécution de la méthode de Lanczos modifiée.

On applique le solveur itératif AEBEIS (voir [7.8]) pour générer des vecteurs de Lanczos. La technique FIC (Factorisation incomplète de Cholesky) est conseillée pour les préconditionnements multi-niveaux [7,8,18-20] ou simple niveau. Elle garantit la rapidité des opérations pendant le calcul d'un produit matrice-vecteur et la résolution rapide de préconditionnements. Attention, la tolérance retenue pour le solveur itératif (Préférences du projet > Analyse de structure > Paramètres) détermine la précision de l'évaluation des vecteurs de Lanczos. En principe, une valeur de 1,0e-04 est suffisante. Plus le nombre de modes est important, plus les vecteurs de Ritz bas seront proches des modes propres correspondants, et plus la somme des masses modales sera complète.

Méthode du Gradient conjugué préconditionné (PCG)

On recommande la méthode PCG [9-13] pour définir un petit nombre de modes propres dans le mode Modal en cas d'application d'un solveur itératif. Elle peut servir à affecter une charge de vent ou pour vérifier quelques modes bas obtenus par la méthode PCG_Ritz. Tous les types de préconditionnement (Outils > Préférences > Itératif > Paramètres) définis pour l'analyse statique sont disponibles. Tous les types de matrice des masses (Homogène, Simplifiée avec rotations, Simplifiée sans rotations) sont disponibles.

La méthode du gradient conjugué préconditionné repose sur la minimisation directe du quotient de Rayleigh

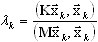(A11)

au moyen d'une approche du gradient où : K - numéro d'itération, λ_k - approximation correspondante d'une valeur propre. L'approche du gradient recherche la valeur du paramètre α_k qui extrait la valeur minimale de λk de (A11) :

(A12)

où p_k est un vecteur de direction conjugué. La recherche de la valeur de α_k [voir 9-13] donne :

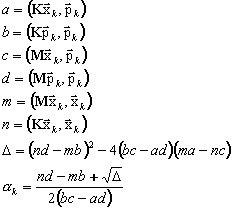
On applique le préconditionnement B pour accélérer la convergence

B z_k+1 = r_k+1 -> z_k+1 (A13)

La direction du gradient est définie comme suit :

(A14)

La nouvelle direction conjuguée est définie comme suit :

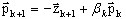(A15)

où

Les itérations continuent jusqu'à ce que

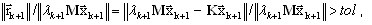(A16)

où tol est la tolérance désirée. En général, tol = 1,0e-02 assure une précision très satisfaisante à l'usage des ingénieurs. Il convient de garder à l'esprit que le rapport de convergence (A16) est calculé en norme très forte (voir rubrique couvrant la précision des calculs). La tolérance indiquée ci-dessus autorise une précision de valeurs propres d'au moins 1,0e-04.

En cas de convergence d'un premier couple propre, celui-ci est stocké en tant que résultat final. Les calculs des premières itérations visant à obtenir le couple propre suivant débutent alors. On utilise la procédure d'orthogonalisation des vecteurs propres définis précédemment à chaque pas d'itération, pour éviter le doublement des couples propres. On applique cette procédure jusqu'à l'obtention de tous les couples propres souhaités.

La méthode d'accélération de convergence la plus efficace pour PCG commence par un bon préconditionnement. Tous les types de préconditionnement liés aux solveurs itératifs sont disponibles pour la méthode PCG. Il est fortement conseillé d'appliquer le préconditionnement multi-niveaux [18-20] ou le préconditionnement simple avec lissage par FIC [9 à 12] en cas d'utilisation d'un solveur AEBEIS [7.8].

Méthode de Ritz-Gradient (PCG_Ritz)

La méthode PCG_Ritz [8] permet de définir rapidement un ensemble de vecteurs de Ritz en pseudo-mode, quand un solveur itératif est sélectionné. Cette approche est souvent efficace en analyse sismique ou spectrale de structures de taille moyenne (de 10 000 à 60 000 équations).

Elle repose sur la génération d'un système orthogonal de vecteurs de base. On applique la méthode du gradient avec préconditionnement multi-niveaux sur la base d'une technique "élément par élément" pour réduire le quotient de Rayleigh à chaque étape de la préparation des vecteurs de base. Elle garantit l'évolution du vecteur de base obtenu vers le mode propre le plus bas sans agrégation ni décomposition d'une matrice de rigidité étendue. Une telle méthode est souvent très efficace pour l'analyse en réponse dynamique par rapport la méthode classique de superposition modale, surtout en analyse de réponse sismique. La méthode proposée permet d'appliquer des types arbitraires d'éléments finis dus à l'approche par agrégation, et propose une solution rapide et réduit les exigences en termes de stockage sur disque par rapport à la technique "élément par élément". Cette méthode est particulièrement efficace pour les matrices de masses cohérentes.

Soit le problème de valeur propre suivant :

Kφ - λM φ = 0 (A17)

où K, M représente les matrices de rigidité et des masses, φ est le vecteur propre et λ, la valeur propre. La procédure d'évolution de l'ensemble de vecteurs de base x0, x1, …, xn, vers le mode propre le plus bas fera l'objet d'une description. On applique la méthode du gradient préconditionné pour réduire le quotient de Rayleigh

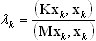(A18)

où 0 ≤ k ≤ n, k étant le numéro du pas d'évolution, n+1 est le nombre de vecteurs de base définissant la taille du sous-espace appartenant à (x0, x1, …, xn); n + 1 << N, où N représente le nombre de degrés de liberté du problème étudié (A17). Bien souvent, le problème de valeurs propres étudié est mal conditionné. L'évolution du vecteur de base obtenu xk vers le mode propre le plus bas est alors très lente. On applique l'opérateur de préconditionnement B pour corriger ce phénomène. L'expression B z_k = r_k -> z_k indique la résolution d'un système d'équation de vecteurs en correspondance zk, où B est un opérateur de préconditionnement et r_k = Kx _k - λ_k M x_k est un vecteur résiduel correspondant.

Les vecteurs de base remplissent les critères d'orthogonalité suivants :

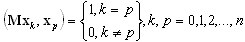(A19)

Le problème source de valeurs propres de grande échelle (A17) est ramené au problème de valeurs propres de sous-espace

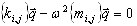(A20)

Les matrices de projection du sous-espace sont définis comme suit : {k_ij} = {Kx_i, x_j} et {m_ij} = {Mx_i, x_j} = U, où U est une matrice unitaire.

Les vecteurs de Ritz v₁, v₂, …, v_n+1 pour les vecteurs de base dérivés x0, x1, …, xn et approximations de fréquences correspondantes ω₁, ω₂, …, ω_n+1 sont utilisés pour la superposition de la réponse dynamique structurelle.

La procédure d'évolution des vecteurs de base x_k, k = 0, 1,..., n vers le mode propre le plus bas est très proche de l'étape correspondante dans la méthode d'itération du gradient préconditionné utilisée pour résoudre le problème de valeurs propres. La convergence des méthodes d'itération préconditionnées est connue pour dépendre fortement des propriétés de l'opérateur préconditionné B. Cet opérateur doit être défini à l'avance, car il facilite la résolution de B z_k+1 = r_k+1 et remplit la condition C ( B^-1 K) -> 1 de la meilleure façon possible.

La dernière condition posée par la méthode de Ritz-gradient assure une bonne approximation des modes propres inférieurs.

Cette méthode est proposée uniquement pour l'approche itérative à plusieurs niveaux, qui offre un préconditionnement satisfaisant. On utilise les techniques de préconditionnement EPE (élément par élément) et FIC. La qualité des vecteurs de Ritz générés de cette manière est très variable, selon les propriétés de l'opérateur de préconditionnement B (voir A13 et [8]). Puisque l'approximation des modes de vibration inférieurs donnée par le modèle grossier est satisfaisante, les vecteurs de Ritz de niveau plus fin constituent une bonne approximation des vecteurs propres correspondants (voir [8]). La qualité des résultats obtenus par une telle méthode dépend donc énormément de capacité du modèle grossier à conserver la similarité par rapport au modèle d'éléments finis MEF (appelé niveau fin). Un seul niveau d'agrégation assure généralement une bonne approximation. À partir de deux niveaux d'agrégation, la qualité des résultats n'est pas garantie. C'est la principale limite de l'application de cette méthode dans l'analyse d'un système étendu de plus de 60 000 équations.

Si la matrice de préconditionnement B = K (le niveau grossier est identique au niveau fin), on passe alors de la méthode de Ritz-gradient à la méthode Lanczos (voir [8]). Des explications mathématiques figurent en partie [8].

Analyse modale - Précision des calculs

Le problème de valeurs propres généralisé est défini comme suit :

Kφ - λM φ = 0 (A17)

où K, M désignent respectivement les matrices de rigidité et des masses, {φ, λ} - couples propres (mode de vibration naturel et valeur propre). Deux types de vecteurs résiduels sont définis :

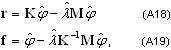
où {φ, λ} sont des couples propres réellement calculés contenant des erreurs de calcul. La première expression définit un vecteur résiduel en termes de forces. La seconde le définit en termes de déplacements.

On utilise quatre critères pour estimer les erreurs de calculs de vecteurs propres.

• . Ce critère est très strict. Généralement, si ε ≤ 0,01, les quatre premiers chiffres de la valeur propre sont définis avec exactitude. On l'applique uniquement pour la PCG, si un solveur itératif a été retenu.
• e = (r, φ). Ce critère est un peu moins strict que le précédent. On le retient dans le cadre de la méthode de Lanczos modifiée, si le solveur itératif a été choisi.
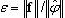• . Ce critère est qualifié de souple car la convergence des déplacements en une situation d'éléments finis donnée est souvent plus rapide que la convergence des forces internes. On l'utilise pour les méthodes BLSI, SI et Lanczos dans le cas de sélection d'un solveur Skyline ou direct.
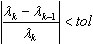• -, où λk, λk-1 sont deux valeurs propres successives pour les (k)-ème et (k-1)-ème pas de l’itération, et tol est la tolérance définie dans la boîte de dialogue Paramètres de l’Analyse Modale. On l'utilise comme critère intermédiaire pendant l'exécution des méthodes BLSI, SI et Lanczos (avec solveurs Skyline ou direct) dans le mode modal. Ce critère, très rapide, n'est cependant pas d'une fiabilité absolue. Utiliser (4) permet de réduire considérablement le temps de calcul pour les méthodes BLSI, SI et Lanczos, surtout pour les systèmes importants. À l'issue d'une analyse de valeur propre, le critère (3) s'applique en tant que vérification finale de la précision. L'utilisateur doit se reporter à la colonne "Précision" du tableau où figure la valeur 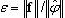. En cas de précision insuffisante, il faut recommencer l'analyse de valeur propre avec une tolérance accrue pour les valeurs propres tol..

Le tableau suivant récapitule les points mentionnés ci-dessus. Le symbole n.c. indique que la vérification de convergence correspondante n'est pas réalisée. Les résultats de la vérification finale sont obtenues une fois (une seule) et figurent dans la colonne "Précision" du tableau. Le contrôle de convergence en cours de calcul est réalisé à plusieurs reprises.

	Solveurs directs		Solveur itératif
Type de critère	BLSI, SI, Méthode de Lanczos	Méthode de réduction de la base	Méthode de Lanczos modifiée	PCG_Ritz	PCG
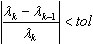
Pendant les calculs		n.c.	n.c.	n.c.
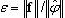
Vérification finale		n.c.	e = (r, j)	n.c.

Il convient d'indiquer que la méthode Lanczos pour le mode sismique génère un contrôle de convergence 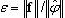à travers chacun des 20 pas de Lanczos. La méthode de réduction de la base et la méthode PCG_Ritz sont des méthodes de Ritz. Comme il ne s'agit pas de l'approche itérative, sa précision n'est pas vérifiée.

S'il s'avère que la précision de certains modes après calcul est insuffisante, les éléments suivants sont nécessaires :

Solveurs directs		Solveur itératif
BLSI, SI, Méthode Lanczos - Mode modal	Méthode de réduction de la base	Méthode de Lanczos modifiée	PCG_Ritz	PCG
Diminuez la tolérance dans la boîte de dialogue Paramètres d'analyse modale	Augmentez le nombre de noeuds et de directions de base.	Augmentez le nombre de modes. Diminuez la tolérance dans la boîte de dialogue Paramètres du solfeur itératif	Augmentez le nombre de modes. Diminuez le nombre de niveaux d'agrégation. Augmentez le nombre d’itérations internes.	Diminuez la tolérance dans la boîte de dialogue Paramètres d'analyse modale

Annexe 3B

L'approche du pseudo-mode

Les équations de mouvement de la source pour les charges sismiques deviennent alors :

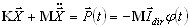(B1)

K, M, les matrices de rigidité et des masses ;

I dir (vecteur unitaire de direction) - φ(t) - comportement temporel de l'accélération du sol

On recherche la solution ainsi :

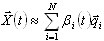(B2)

où q_i sont les vecteurs de base de taille Neq - nombre d'équations du modèle source des éléments finis.

Ces vecteurs doivent répondre aux critères suivantes :

• conditions aux limites cinématiques et statiques.
• indépendance linéaire
• complétude de la base.

On peut adopter soit les vecteurs de Lanczos ou tous vecteurs obtenus pour les forces nodales ponctuelles unitaires (méthode de réduction de base pour solveurs directs ou méthode Ritz-gradient ou PCG_Ritz).

On a alors la projection dans le sous-espace suivant :

Notons que β est de taille N, la matrice Q est de taille NeqxN.

Les équations sub-spatiales (B3) seront résolues par décomposition des vecteurs propres (dans le sous-espace tel que Q = {q1, q2, …, qN}).

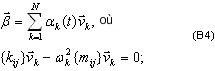
Notons que la décomposition (4) est une expression exacte, le sous-script K admettant des valeurs comprises de 1 à N sur l'intégralité du sous-espace Q.

Le changement de (B4) en (B3) aboutit à un ensemble d'équations non couplé

Soient :

(B6)

(B5) devient alors :

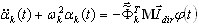(B7)

où k=1,2,..., N.

Appliquons la méthode Spectre de réponse aux équations non couplées (B7)

(B8)

où indiquent la réponse maximale pour le mode sub-spatial K et la fonction d'accélération spectrale.

Changeons (B8) en (B4) puis en (B2) :

(B9)

Notons que pour N - > Neq :

ω_k -> Ω_k

Où Ωk, sont le couple propre exact du problème propre des éléments finis source.

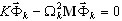(B10)

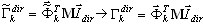et où 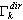est le coefficient de masse participante pour le mode propre k.

Conclusions

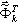1. L'approche proposée ne nécessite pas les "bonnes" approximations , ω_k -> Ω_k. Il se peut que , ω_k se rapprochent de , Ω_k avec une précision arbitraire.
2. L'approche proposée n'est pas pire que la méthode de décomposition modale bien connue (superposition). Ces deux méthodes constituent des cas particuliers de la méthode de projection commune et convergent vers la solution "exacte" quand N - > Neq. (Cette affirmation n'est pas exactement valable pour la méthode Spectre de réponse, car elle est de nature statistique et sa convergence vers la solution exacte se produit quand N - > ∞. Il est évident que N > Neq risque de provoquer un conflit, le nombre de vecteurs de base ne pouvant pas dépasser Neq. Il est donc possible d'obtenir différentes solutions pour les vecteurs de base quand N = Neq. Il s'agit d'une particularité de la méthode Spectre de réponse. Pour les méthodes autres que Spectre de réponse, la convergence complète se produit quand N = Neq. La convergence pour le cas de la méthode Spectre de réponse n'a qu'une valeur statistique, car elle constitue une approche statistique visant à obtenir une résolution moyenne si le comportement temporel a été perdu. C'est pour cela que le terme "solution exacte" est à utiliser avec précaution).
3. Quelle est le meilleur type de base : vecteur de Ritz ou vecteurs propres ? On doit pouvoir trouver une base qui offrirait une meilleure convergence vers la solution "exacte" (N = Neq) en utilisant le plus petit nombre de fonctions de base N. Cette question sera résolue par l'examen d'exemples pratiques.

   En général, la première partie de couples 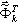, ω_k donnent de bonnes approximations pour les couples propres correspondants , Ω_k (il est possible de déterminer la précision de chaque couple dans la colonne "Précision" de la liste de sortie). Seule la dernière partie de couples 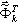, ω_k associe de mauvaises approximations aux couples propres exacts et peut être considéré comme "Pseudo-mode" (conformément à la norme sismique française PS-92).

4. L'utilisation de l'intégralité du sous-espace Q = {q1, q2, …, qN} garantit l'augmentation rapide des masses participantes. En mode Modal et Sismique, seule une partie de ce sous-espace est utilisé.

Annexe 3C

Exemples d'application des modes Sismique et Pseudo-mode.

La variété des types de problèmes sismiques et spectraux où le pourcentage des masses est insuffisant (70 % à 90 %) est évidente. Ces "bons problèmes" peuvent être résolus à l'aide de méthodes bien connues.

• En affectant un nombre arbitraire de N modes.
• En calculant les N premiers modes séquentiels en passant en mode Modal.

Toutefois, pour les problèmes difficiles, cette approche peut s'avérer inaccessible. Prenons, par exemple, les problèmes Coreal ou Musée. Il s'agit de modèles d'éléments finis préparés par des ingénieurs français. On présente un pourcentage de masses pour plusieurs séries de modes propres définis. On utilise le mode Modal (méthode Lanczos).

Historique de convergence du problème Coreal

Nombre de modes convergents	% Masses
44	< 1%
62	12%
75	38%
89	60%
116	74%
154	77%
179	80%

Historique de convergence du problème Musée

Nombre de modes convergents	% Masses
41	20%
106	40%
119	42%

Par exemple, 80 % signifie que pour deux directions données, les sommes des masses sont au moins égales à la valeur donnée. Le mode Modal génère des modes propres, pendant que l'on atteint soit le pourcentage des masses indiqué, ou la limite supérieure indiquée comme nombre maximal de modes. On obtient la solution finale de la méthode Spectre de réponse sous la forme d'une superposition statistique de vecteurs propres.

Dans les deux problèmes étudiés, le nombre de degrés de liberté est inférieur à 2 000. On dit de tels problèmes qu'ils sont "petits" (en raison du nombre de degrés de liberté). Pour les problèmes moyens à grands, il est possible que les modes Modal et Sismique ne puissent pas s'appliquer dans la pratique, en raison de longueur interminable des calculs. Pour de tels cas, on recommande l'application du Pseudo-mode. Voici, ci-dessous, le comportement temporel de la convergence des problèmes Coreal et Musée.

"Historique de convergence" du problème Coreal

Nombre de vecteurs de base	% Masses
10	58%
20	67%
40	70%
80	80%

"Historique de convergence" du problème Musée

Nombre de vecteurs de base	% Masses
10	60%
20	66%
40	71%

Remarque : Il faut définir de 130 à 150 vecteurs de Lanczos pour obtenir 80 vecteurs propres pour le mode modal. Les temps de calcul en pseudo-mode est de 3 à 5 fois plus courts.

La convergence des résultats en pseudo-mode est illustrée dans le problème suivant. Le tableau ci-dessous présente le résultat des valeurs min./max. de la combinaison CQC pour les modes Modal et Pseudo.

Mode	UX (cm)	UY (cm)	UZ (cm)	% masse.
Modale	5,52002e-00	5. 88293e-00	5,83013e-00	81%
Pseudo, Nvect. = 10	5,58710e-00	5. 89055e-00	5,00224e-00	80%
Pseudo, Nvect. = 20	5,52937e-00	5,88870e-00	6,08661e-00	91%

Nvect - Nombre de vecteurs de base.

Annexe 3D

Application de méthodes d'analyse modale pour résoudre des systèmes étendus

Exemple 1

Comparaison des temps de calcul pour les méthodes BLSI et Lanczos. On considère des nombres de modes propres distincts.

Solveur appliqué : solveur direct. Type de matrice des masses : Simplifiée avec rotations.

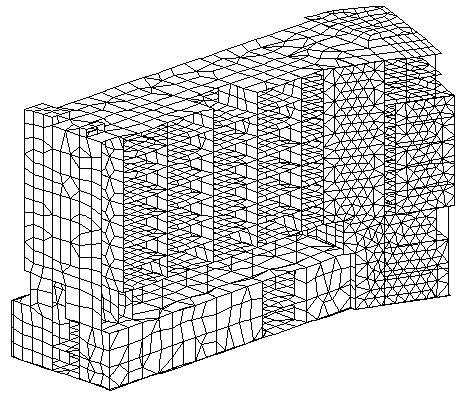
Fig. D1. Cas d'un hôtel. Nombre de noeuds : 6 359 - Nombre d'éléments : 7 264 - Nombre d'équations : 37 806.

Tableau D1. Comparatif des résultats

BLSI		Lanczos
f (Hz)	Précision	F (Hz)	Précision
2,794e-001	1,082e-006	2,794e-001	5,680e-015
1,388e+000	1,389e-004	1,388e+000	2,199e-013
1,520e+000	7,847e-004	1,520e+000	8,193e-012
1,644e+000	2,469e-004	1,644e+000	4,497e-013
1,747e+000	2,691e-004	1,747e+000	5,455e-014
1,776e+000	3,092e-004	1,776e+000	9,127e-013
1,806e+000	3,153e-004	1,806e+000	6,621e-013
1,818e+000	6,383e-004	1,818e+000	3,656e-012
2,622e+000	1,565e-003	2,343e+000	2,047e-011
2,634e+000	1,383e-003	2,622e+000	1,223e-005

La vérification de Sturm n'étant pas lancée, on a un couple propre ignoré entre les 8^ème et 9^ème modes, si BLSI est appliqué.

Tableau D2. Durée de l'extraction du mode (en secondes)

Méthode	10 modes	50 modes	100 modes
BLSI	735	6029	23572
Lanczos	1472	12637	25271

Factorisation de la matrice : 841 sec.

L'association de méthodes avancées (BLSI, Lanczos) et d'un solveur direct puissant permet une factorisation matricielle rapide et d'extraire un grand nombre de modes propres. Les calculs ont été réalisés sur un ordinateur P350 (256 Mo de RAM).

Exemple 2

Application de différentes méthodes pour la résolution du problème PJG203. Le modèle contient des liaisons rigides impliquant l'utilisation d'une matrice de masses homogène. 25 pseudo-modes ont été extraits.

Fig. D2. Problème PJG203. Nombre de noeuds : 5 945 - Nombre d'éléments : 11 471 - Nombre de liaisons rigides : 22 - Nombre de noeuds compatibles : 302 - Nombre d'équations : 34 266.

Tableau D3. Temps de calcul, espace occupé sur le disque, dix premières fréquences et précision correspondante de différentes méthodes.

Méthode	Temps (sec.)	Disque dur (Mo)	Fréquences (Hz)	Précision
Skyline	61 633	597	1,175e+000 1,337e+000 1,454e+000 2,445e+000 2,445e+000 2,628e+000 2,829e+000 3,033e+000 3,209e+000 3,595e+000	8,043e-015 1,025e-013 1,031e-013 1,712e-006 5,566e-006 6,331e-008 3,538e-001 3,052e-005 9,086e-005 4,498e-003
Direct	4 435	99	1,175e+000 1,337e+000 1,454e+000 2,445e+000 2,445e+000 2,628e+000 2,825e+000 3,033e+000 3,209e+000 3,595e+000	3,522e-012 2,689e-011 1,159e-010 1,735e-006 5,639e-006 6,419e-008 3,520e-001 3,034e-005 9,938e-005 4,386e-003
Modif. Lanczos	3 459	24	1,175e+000 1,337e+000 1,454e+000 2,445e+000 2,445e+000 2,628e+000 2,791e+000 3,033e+000 3,209e+000 3,595e+000	3,719e-004 3,891e-004 6,601e-004 1,454e-003 1,875e-003 2,946e-003 3,364e-003 3,923e-003 2,175e-002 1,580e-001
PCG_Ritz	1 521	24	1,266e+000 1,350e+000 1,467e+000 2,445e+000 2,446e+000 2,446e+000 2,805e+000 3,035e+000 3,381e+000 3,566e+000	n.c. - PCG_Ritz n'est pas une méthode itérative. Il s'agit d'une méthode Ritz. Par conséquent, on obtient des pseudo-modes au lieu de modes propres "exacts".

Les paramètres suivants ont été retenus pour la méthode Lanczos modifiée : solveur itératif AEBEIS (à plusieurs niveaux); Préconditionnement FIC; 2 niveaux d'agrégation; 4 itérations internes; tol. = 1.0e-04 - précision de génération de vecteurs de Lanczos.

Les paramètres suivants ont été retenus pour la méthode PCG_Ritz : solveur itératif AEBEIS à plusieurs niveaux ; Préconditionnement FIC ; 1 niveau d'agrégation ; 4 itérations internes.

Les fréquences convergentes sont indiquées en rouge. Si la précision (voir Annexe 3A) d'une norme relative de vecteur résiduel pour un mode donné est inférieure à 5,0e-02, une telle norme peut être considérée comme totalement convergente pour la vecteur propre correspondant. Les fréquences indiquées en rouge sont donc considérées comme les valeurs exactes d'un modèle discret donné. L'estimation de l'erreur de la méthode PCG_Ritz figure dans le tableau D4. On peut conclure de ce qui précède que les résultats obtenus par la méthode PCG_Ritz permettent aux ingénieurs d'obtenir une approximation suffisamment bonne, et que cette approche est exploitable pour l'étude du comportement sismique.

Les méthodes avancées permettent de réduire considérablement le temps de calcul et l'espace occupé sur le disque, sans que l'exactitude en souffre réellement.

Tableau D4. Erreur d'évaluation de la méthode PCG_Ritz

Fréquence "exacte"	Résultats PCG_Ritz	Erreur (%)
1,175e+000	1,266e+000	7.7
1,337e+000	1,350e+000	1.0
1,454e+000	1,467e+000	0.9
2,445e+000	2,445e+000	0.0
2,445e+000	2,446e+000	0.0
2,628e+000	2,446e+000	7.0
2,791e+000	2,805e+000	0.5
3,033e+000	3,035e+000	0.1
3,209e+000	3,381e+000	5.4
3,595e+000	3,566e+000	0.8

Les calculs ont été effectués sur un ordinateur PC-450 (128 Mo de RAM).

Exemple 3

Soit une fine dalle carrée avec matrice de masses homogène sur une arête. Soient une coque à 4 noeuds et un maillage 128x128 (nombre d'équations Neq : 99072). Les 40 pseudo-modes sont extraits.

Le Tableau 5 compare les temps de calcul et l'occupation du disque pour les méthodes Lanczos (Skyline et direct), Lanczos modifiée (solveur itératif) et Ritz-gradient (PCG_Ritz).

Tableau D5. Temps de calcul et espace occupé sur le disque pour plusieurs méthodes.

Méthode	Temps (sec.)	Disque dur (Mo)
Lanczos (solveur Skyline)	141 559	7 367
Lanczos (solveur direct)	15 615	157
Lanczos modifiée (solveur itératif)	18 978	0
PSG_Ritz	9 651	192

Les calculs ont été effectués sur un ordinateur PC-450 (128 Mo de RAM).

Les dix premières fréquences obtenues par Lanczos (Skyline ou direct), Lanczos modifée (solveur itératif, préconditionnement FIC, 3 niveaux d'agrégation, 8 itérations internes, tolérance de 1,0e-03 pour la génération de vecteurs de Lanczos) sont identiques. La précision des calculs étant très élevée, on peut considérer ces valeurs comme exactes pour le modèle discret donné. C'est valeurs servent de références pour l'estimation de l'erreur pour les fréquences obtenues par la méthode PCG_Ritz. L'approche à plusieurs niveaux avec préconditionnement FIC (1 niveau d'agrégation, 4 itérations internes) a été sélectionnée conjointement à l'application de la méthode PCG_Ritz. Les résultats correspondants figurent dans le tableau D6.

Tableau D6. Comparaison des fréquences pour les méthodes PCG_Ritz et Lanczos

Fréquences par Lanczos (Hz)	Précision	Fréquences par PCG_Ritz (Hz)	Erreur (%)
3,722e+000	5,918e-014	3,725e+000	0.08
9,112e+000	4,474e-014	9,115e+000	0.03
2,282e+001	2,424e-012	2,284e+001	0.09
2,915e+001	5,866e-013	2,915e+001	0.00
3,315e+001	1,795e-013	3,318e+001	0.09
5,801e+001	2,373e-011	5,803e+001	0.03
6,565e+001	3,028e-011	6,571e+001	0.09
6,873e+001	6,907e-014	6,875e+001	0.03
7,602e+001	1,549e-012	7,609e+001	0.09
9,949e+001	3,302e-013	9,953e+001	0.04

Exemple 4

Soit un bâtiment de grande taille (voir Fig. D3)

Fig. D3 Bâtiment de grande taille Nombre de noeuds : 26 126 - Nombre d'éléments : 30 272

Nombre d’équations : 155 920.

On a choisi l'analyse statique linéaire (un seul cas de charge) et l'extraction de 10 modes propres. La tolérance retenu pour le solveur itératif est égale à 1,0e-04. On associe le solveur Skyline à la méthode Lanczos. On associe le solveur direct aux méthodes Lanczos et BLSI. On associe la méthode Lanczos modifiée au solveur itératif (méthode à plusieurs niveaux, avec 3 niveaux d'agrégation, 4 itérations internes et préconditionnement FIC). La matrice des masses est de type Simplifiée avec rotations.

Tableau D7. Temps de calcul et espace occupé sur le disque pour plusieurs méthodes.

Méthode	Espace disque (Mo)	Statique linéaire (cdr seuls) (s)	Extraction de 10 modes propres (sec.)	Durée totale (sec.)
Skyline	5 702	136 065	65 052	203 878
AEBEIS	52	2 442	25 793	28 355
Direct (méthode Lanczos)	773	10 253	24 500	35 762
NS direct (méthode BLSI)	773	10 253	11 534	22 604

Les calculs ont été effectués sur un ordinateur PC-450 (128 Mo de RAM).

Conclusions

L'association de méthodes avancées BLSI ou Lanczos et d'un solveur direct ou d'un solveur itératif performant AEBEIS avec préconditionnement FIC constitue de puissants outils pour résoudre des problèmes de valeurs propres ou des problèmes statiques linéaires importants. Ils réduisent considérablement le temps de calcul et l'espace occupé sur le disque, en comparaison du solveur Skyline conventionnel. La méthode PCG_Ritz est une approche rapide permettant d'estimer le comportement sismique de la structure donnée. Quand un seul niveau d'agrégation est accepté, les résultats correspondants, obtenue par la méthode PCG_Ritz sont proches de ceux obtenus par les méthodes Lanczos ou BLSI.

Références

1. E.L.Wilson. An eigensolution strategy for large systems. Computers&Structures, Vol.16, No. 1 à 4, pp.259-265, 1983.
2. Wilson. A new method of dynamic analysis for linear and nonlinear systems. Finite Elements in Analysis and Design, 1, 1985, 21-23, North-Holland.
3. E.L.Wilson, Three dimensional dynamic analysis of structures, Computers and Structures, Inc., Berkeley, Californie, États-Unis, 1996.
4. R.W.Clough, J.Penzien. Dynamics of Structures. McGraw-Hill Book Comp., 1975, 634 p.
5. Fialko S. Yu. Investigations of the Initial Imperfections Influence to Natural Vibrations of Ribbed Conical Shells, Soviet Applied Mechanics, 1982, 18, N11, pp.118 - 122. (en russe)
6. Fialko S. Yu. Nonsteady vibrations of ribbed conical shells under the influence of local loads, Soviet Applied Mechanics, 1987, v23, N6, p. 547-552.
7. Fialko S.Yu. High-performance aggregation element-by-element iterative solver for large-scale complex shell structure problems. Archives of Civil Engineering, XLV, 2, 1999. P.193-207.
8. Fialko S.Yu. High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis. CAMES (Computer assisted mechanics - engineering sciences), IV, 2000
9. Gambolati G., Pini G., Sartoretto F., An improved iterative optimization technique for the leftmost eigenpairs of large symmetric matrices, J. Comp. Phys., 74: 41 - 60, 1988.
10. Sartoretto F., Pini G., Gambolati G., Accelerated simultaneous iterations for large finite element eigenproblems, J. Comp. Phys., 81: 53 - 69, 1989.
11. Papadrakakis. A partial preconditioned conjugate gradient method for large eigenproblems, Comp. Meth. Appl. Mech. Eng., 62: 195 - 207, 1987.
12. Papadrakakis, Solving large -scale problems in mechanics, John Wiley & Sons Ltd., 1993.
13. S.Bitzarakis, M.Papadrakakis, A.Kotsopulos. Parallel solution techniques in computational structural mechanics. Comp. Methods Appl. Mech. Engrg. 1997, 148, p.75-104.
14. Hughes T.J.R., Ferencz M. Implicit solution of large-scale contact and impact problems employing an EBE preconditioned iterative solver, IMPACT 87 Int. Conference on Effects of Fast Transient Loading in the Context of Structural Mechanics, Lausanne, Suisse, août 26-27, 1987.
15. Hughes T.J.R., R.M.Ferencz et j.O.Hallquist. Large-scale vectorized implicit calculations in solid mechanics on a CRAY X-MP/48 utilizing EBE preconditioned conjugate gradients, Comput. Meths. Appl. Mech. Engrg., 61
16. Hughes Th. J. R. "The Finite Element Method. Linear Static and Dynamic. FEM Analysis."
17. Parlett B.N., 1980. "The Symmetric Eigenvalue Problem". Prentice-Hall, Inc., Englewood Cliffs, N.J. 07632.
18. Bulgakov, V.E., Belyi, M.E., Mathisen, K.M. Multilevel aggregation method for solving large-scale generalized eigenvalue problems in structural dynamics, Int. j. Numer. Methods Eng., 40: 453 - 471, 1997.
19. Bulgakov, V.E. Iterative aggregation technique for large-scale finite element analysis of mechanical systems, Comput. Struct, 52: N4, 829-840, 1994.
20. Bulgakov, V.E., G. Kuhn. High-performance multilevel iterative aggregation solver for large finite-element structural analysis problems, Int. j. Numer. Methods Eng., 38: 3529-3544, 1995.
21. Regulatory Guide
22. I.Ja.Amiro, V.A.Zarucky, V.N.Revutsky, Yu.V.Skosarenko, A.I.Telalov, S.Yu.Fialko. Oscillations of Ribbed Shells of Revolution, Kiev, Naukova Dumka, 1988, 169 p. (en russe).
23. S.Yu.Filako. Natural Vibration Modes of Ribbed Conical Shells, Soviet Applied Mechanics, 1984, v20, N11, p. 1033-1037. (en anglais)