L’analyse non-linéaire consiste à appliquer les charges de façon incrémentale. Cela signifie que les charges ne sont pas prises en compte à un instant donné dans les calculs, mais qu'elles augmentent graduellement et que les états d’équilibre successifs sont résolus.
Le comportement non-linéaire d'une structure peut être lié à un simple élément de la structure (non-linéarité structurelle ou matérielle) ou dû au rapport non-linéaire entre les efforts et la déformation de la structure entière (non-linéarité géométrique).
Les éléments non-linéaires suivants peuvent entraîner une non-linéarité structurelle :
- Éléments en compression ou traction
- Éléments de type câble
- Contraintes non linéaires (contraintes unilatérales ou définies à l'aide de la fonction de rigidité : appuis, relâchements, nœuds compatibles)
- Plasticité du matériau
- Rotules non-linéaires.
Options de non-linéarité géométrique
Ces options prennent en compte les effets réels d'ordre supérieur et améliorent souvent la convergence des calculs pour les structures contenant des éléments non-linéaires.
- Analyse P-Delta
- Cette analyse prend en compte les effets de second ordre, tels que la modification de la rigidité de l’élément sous l'influence de l’état de contraintes dans l’élément. Elle prend également en compte la génération de moments dus aux efforts axiaux dans les nœuds déplacés horizontalement.
- Analyse Déplacements importants
- Cette analyse prend en compte les effets de troisième ordre, tels que la rigidité latérale supplémentaire et les contraintes dues à la déformation ou à la rotation. Cet effet prend en compte la génération des forces supplémentaires dans la structure déformée (par exemple, dans la poutre encastrée de deux côtés, les efforts axiaux apparaissent et la flèche est réduite).
Ces paramètres d'analyse peuvent améliorer la convergence du processus de calcul, car ils prennent en compte les effets réels d’ordre supérieur. Cela est particulièrement utile lorsque vous travaillez avec une structure qui contient des éléments non-linéaires.
Deux méthodes peuvent être utilisées pour résoudre un système d'équations non-linéaires : la méthode incrémentale et la méthode Arc-length.
Méthode incrémentale
Si la structure contient des éléments non-linéaires (p. ex. câbles, appuis unilatéraux, plasticité du matériau), les calculs sont automatiquement effectués de façon incrémentale.
Dans la méthode incrémentale, le vecteur de charge du côté droit est divisé en n incréments égaux. Un incrément de charge successif est appliqué à la structure au moment où l’état d’équilibre a été atteint pour l’incrément précédent. La norme pour les forces non équilibrées est donnée pour chaque pas, ce qui permet de suivre le comportement de la relation force-déplacement pour la structure.
La figure suivante présente un exemple de processus non-linéaire utilisant la méthode incrémentale. Les valeurs utilisées lors des calculs non-linéaires sont affichées.
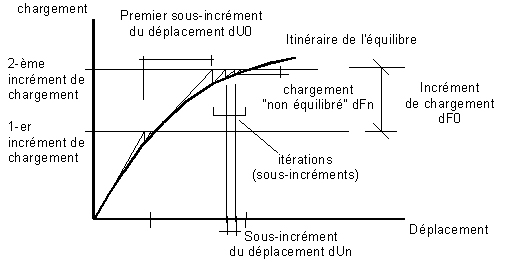
L'incrément de charge est utilisé lors de la division d'une charge en sous-divisions de petite taille. Pour les structures complexes, pour lesquelles l’influence des effets non-linéaires est importante, les calculs peuvent ne pas converger si l’analyse de la valeur d'une charge est appliquée en une seule étape. Le nombre d’incréments de la charge influe sur le nombre d’essais de calcul. Plus le nombre d’incréments est important, plus grande est la probabilité de la convergence des calculs.
Méthode Arc-length
La méthode arc-length (gestion du déplacement) doit être utilisée quand les algorithmes incrémentales de résolution des équations par la gestion des forces ne sont pas convergents.
La méthode Arc-length est utilisée lors de l'analyse pushover non-linéaire. Elle est conseillée quand le modèle de la structure contient les attributs non-linéaires (voir annexe du Manuel Utilisateur).
Processus d'analyse
- La méthode des contraintes initiales.
- La méthode Newton-Raphson modifiée.
- La méthode Newton-Raphson complète.
En général, la méthode des contraintes initiales est la plus rapide tandis que la méthode Newton-Raphson complète est le plus lente. Cependant, la probabilité de convergence est plus élevée avec la méthode Newton-Raphson complète qu'avec la méthode des contraintes initiales.
Le tableau suivant indique comment définir les options de mise à jour de la matrice afin d'utiliser l'algorithme adéquat.
| Algorithme | Mettre à jour la matrice après chaque sous-division | Mettre à jour la matrice après chaque itération |
|---|---|---|
| Contrainte initiale | Inactive | Inactive |
| Newton-Raphson modifiée | Active | Inactive |
| Newton-Raphson complète | Active | Active |
L'algorithme de la méthode de modification BFGS (Broyden-Fletcher-Goldforb-Shanno) permet de modifier la matrice de rigidité lors des calculs. Dans certains cas, l’utilisation de l’algorithme « line search » peut améliorer la convergence de la méthode.
Lorsque l'état d'équilibre est atteint, le processus d'itération s'arrête et le logiciel vérifie la convergence du processus. Les incréments des déplacements dUn et les forces non équilibrées dFn sont alors nuls (c’est-à-dire qu’ils sont inférieurs aux tolérances définies pour les deux valeurs). Le processus d'itération s'interrompt en cas de divergence. L'absence de convergence peut être interprétée comme un effet numérique dû à la surcharge de la structure. De même, l'absence de convergence peut être due à l’instabilité de la procédure numérique (par exemple dans le cas où la charge serait divisée en un nombre d’incréments peu important). Dans un tel cas, le nombre d’incréments de chargement peut être augmenté dans le logiciel, normalement cela aide à obtenir la convergence de la méthode.
Rubrique connexe :
Eléments de type barre dans l’analyse non-linéaire disponible dans Robot.