前に、圧縮下における材料の荷重降下の様子を示す実験データを紹介しました。この荷重降下の大きさを μ と呼ぶことにしましょう。μ の値は、荷重の角度の変化に応じて変化します。したがって、圧縮破損基準を生じさせる任意の応力状態について μ を決定するための方法が必要になります。

0°:

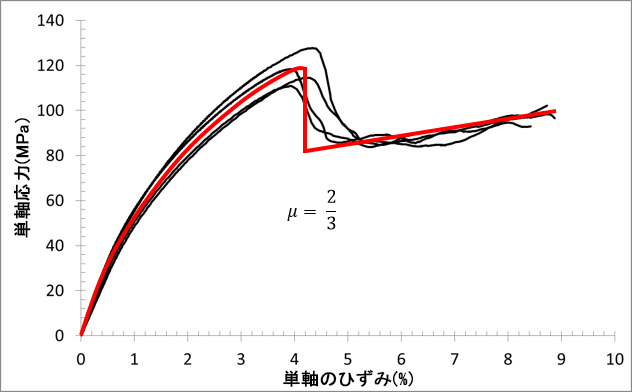
90°:

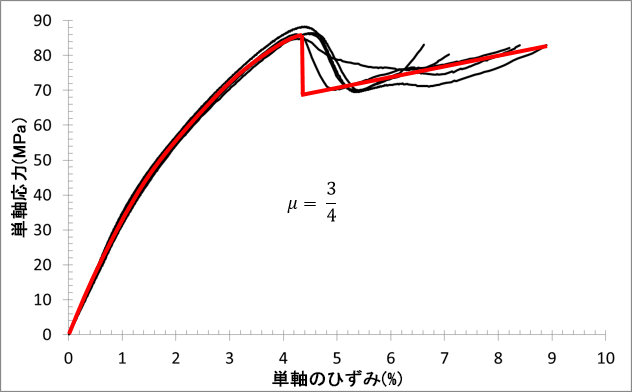
45°:

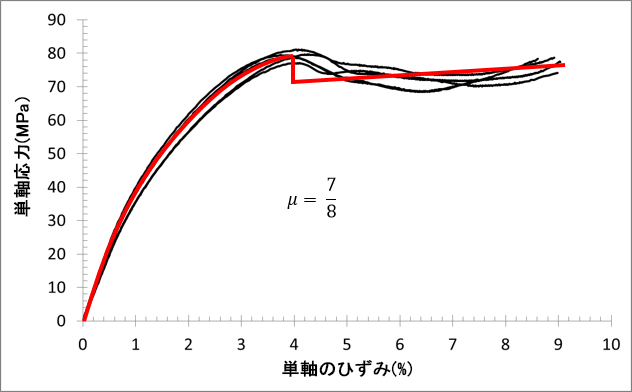
μ を決定する

最初に、圧縮破損基準を生じさせた母材の応力状態の主応力(σI ≥ σII ≥ σIII)と主方向(âI, âII, âIII)を決定します。3 番目の主応力(σIII)は常に、大きさが最大の圧縮応力になります。次に、3 番目の主方向(âIII)と材料の主方向が成す角度を決定します。 この角度を ξ と表記します。

ここで、μ を角度の二次関数として記述します。

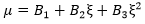
ここで、係数 B1、B2、B3 は、3 つの実験応力-ひずみ応答における荷重降下から決定されます。3 つの既知の入力角度 ξ (0、90、45)に加え、各曲線の計測済み荷重降下 μ を使用して、連立方程式を解いて係数 B1、B2、B3 を決定することができます。これらの係数は構造解析時に使用され、圧縮破損基準をトリガする任意の応力状態に適用する、適切な荷重降下が決定されます。

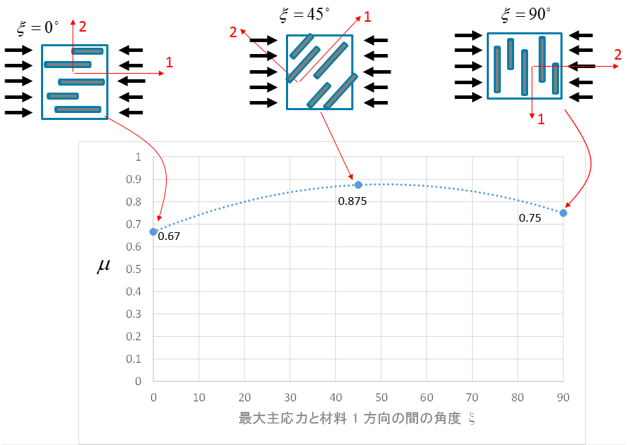
下の図は、μ が、主繊維配向を基準とする主圧縮応力の方向に依存している様子の例を示しています。

損傷の進展

破損を引き起こす応力状態に対して μ を決定した後、複合材料の応力にそれを適用することができます。 複合材料の剛性は、剛性マトリックスを μ の割合で乗じることにより、瞬間的に減少します。 μ が適用された後、以前と同様に塑性応答が進展し続けます。