接着破壊および接着回復速度を予測するために使用される平均母材応力を決定します。

指定された複合応力の状態または応力履歴において、方程式40 に基づく接着破壊速度および方程式41 に基づく接着回復速度を予測します。このプロセスにおける 1 つの明らかな課題は、母材応力テンソルを、KTF を説明する等式で使用できる有効なスカラー応力としてどのように表現するかを決めることです。ある研究者は、疲労寿命を予測するための適切なパラメータは、同じ荷重条件の元で静的強度によって正規化した疲労強度であると示しています[23, 44-45]。これは、しばしば「強度寿命等ランク仮定」と呼ばれます。そこで、有効な疲労応力を決定するために、関数形式の静的破損基準を使用します。

一方向複合材料

一方向複合材料は、単層面における疲労破損について、軸外と軸上の 2 つのモード(またはプロセス)を示します。各プロセスには、固有の有効化エネルギーと有効化体積を使用する必要があります。これは、微小亀裂の蓄積の物理的な特性は、2 つの種類の亀裂の間で異なるためです。また、有効な応力定義も異なります。このセクションでは、軸外荷重と軸上荷重の両方に有効な母材応力を定義します。

軸外

破損基準の形式を検討する場合は、実験で観測された軸外破損モードについて考えると役に立ちます。一方向複合材料の場合、疲労破損はしばしば繊維と並行な亀裂[24, 46]によって生じることが広く報告されています。したがって、繊維と直交する引張力が、これらの平面上のせん断応力とともに疲労における大きな要因となっていることが予測されます。繊維の軸方向を 1 の方向とし、現場の母材破損基準を、以下の形式をとる MCT を使用して計算された母材応力テンソルの横等方性不変量の形式として示します。

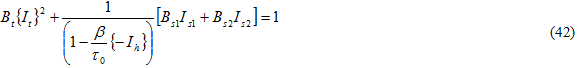
ここで、

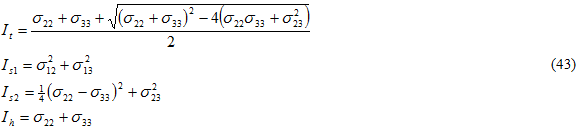
また、{ } はマコーレーの括弧を示し、括弧内の単位量がマイナスの場合、値は 0 (ゼロ)になります。Bi の値は複合材料に対する横方向引張、横方向圧縮および面内せん断の 3 つの静的破損テストにより決定されます。各テストには母材構成の破損が含まれます。方程式 42 を Bs1 で除算すると、有効応力 σeff の形式が求められます。

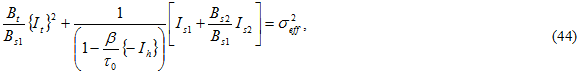
ここで 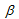は圧力の強化係数で、 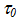は圧力強化のない母材せん断強度です。現在のバージョンでは、すべての計算は 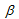= 0\ を使用します。方程式 44 の平方根をとると、方程式40 および 41 に基づく接着破壊を計算するための有効応力が得られます。

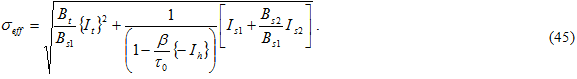
軸上

軸上荷重破損は、繊維/母材のインタフェース部分に生じる母材の亀裂によって発生します。これらの亀裂の大きさは主に軸方向の法線応力によって決まります。したがって、軸上破損(θ = 0°)の場合、有効応力は次のように定義されます。