交番応力が進行性疲労に対してどのように処理されるのかを調べます。

前のページの説明では、応力テンソルを単一のスカラー値に低減する方法について説明しています。ここからは、交番応力を考慮する場合の問題について説明します。応力比 R と平均応力 σm の呼び名は通常、ある最小応力 σmin から最大応力 σmax まで変化する単純な正弦荷重を記述するために導入されます。ここで、

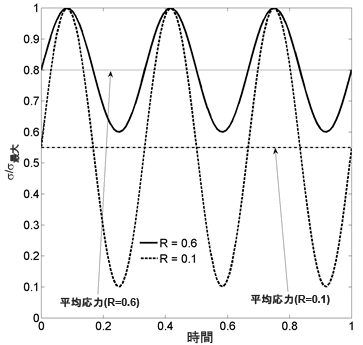
上に示す荷重履歴を、R = 0.1 および R = 0.6 に対して検討します。応力が時間によってのみ変化する量であれば、時間の関数としての接着破壊率は次のように記述されます。

また、接着回復率は次のように記述されます。

式 52 と 53 を積分することで、運動学理論は、σmin を増加させて平均応力を増やした結果、R の値の増加によって疲労寿命が短くなると予測していることがわかります。別の視点として、一定の荷重ケース R = 1 を考えてみます。平均応力を増加させると、故障寿命が明らかに短くなります。しかし、一方向複合材料と織物複合材料の実験によれば、σmin を増やすことで疲労寿命も延びることがわかっています[47, 25-26]。このように、応力の振動特性によって、一定荷重の下では存在しない物理的な特徴が加えられると考えられます。

追加される物理的な特徴は、サイクル処理中の樹脂の温度変化です。純高分子による実験では、交番応力の振幅の増加[28, 35]、または周波数の増加[48]によって樹脂の温度が大きく上昇する結果になりました。運動学理論によって任意の荷重履歴に対する疲労寿命を適切に予測するには、この温度上昇を考慮する必要があります。正弦周期の場合、エネルギー散逸の速度(毎秒) 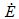は以下により与えられます[28]。

ここで、f は振動周波数、J'' は損失コンプライアンス、σa は応力振幅です。温度の上昇はエネルギー散逸に比例するものと想定します。式40 で使用する温度 T は、基準温度 T* から計算され、以下のようになります。

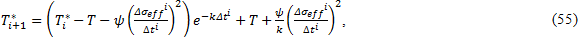
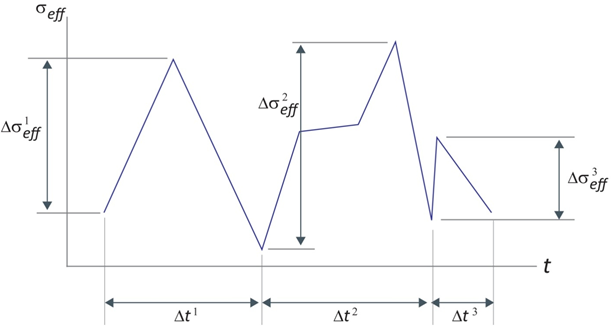
ここで、ψ は比例定数、k はニュートンの冷却の法則、Δσeff は、時間 Δt における有効な応力変化の大きさ、n は周期当たりの異なる応力範囲の数です[26]。以下の図は、Δσeff および Δt の値が、単一の荷重サイクル中にどのように決定されるかを示します。

式 55 内でニュートンの冷却の法則を使用することにより、材料の温度は、長時間の荷重履歴中にその周囲温度で安定し、無限に上昇することはなくなります。