熱活性化プロセス

熱活性化プロセスによって、KTF がどのような影響を受けるかを説明します。

絶対零度より高い温度のすべての原子および分子は、プランクの法則によって表す n 0 に比例する周波数で振動します。

ここで、h はプランクの定数(h = 6.626068 × 10-34­ J-s/K-atom)、kT は熱エネルギーで Boltzmann 定数 k (k = 1.3806504 × 10-23­ J/K-atom)と絶対温度 T の積として表します。しかし、各振動に関連付けられた熱エネルギーは単一の数ではなく、むしろ分布であるため、任意の振動がエネルギーの障壁 U を乗り越え、平衡状態から別の状態に移動するのに十分なエネルギーがある可能性が常にあります。これが任意の振動で発生する可能性は、一般的な指数フォーム 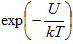によって指定されます。したがって、接着破壊率 K b は単純に次のように記述できます。

破断および疲労解析の目的では、一方の平衡状態が非破壊状態で、他方が破壊状態となります。このプロセスは下の左側の図に視覚的に示されています。したがって、同様の方程式を接着回復についても、次のように記述できます。

次に、方程式(38)で記述された接着破壊率と、方程式(39)で記述された接着回復率に適用される応力の効果を考慮します。このコンテキストでは、単位面積あたりの力ではなく、単位体積あたりのエネルギーの観点から応力を検討する方が有益です。応力が、接着破壊プロセスを促進する作用をしている場合は、接着破壊に対するエネルギーの障害を低減し、接着回復に必要なエネルギーの障害を増加するはずです。

これは材料の体積 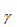、プロセスが発生する活性化体積によって異なります 1。これにより、活性化エネルギーの低減は単に活性化体積と応力の積となります。下の右側の図は、応力が活性化エネルギーを変化させる様子を示しています。適用された応力の効果を反映するために、方程式(38)を次のように修正します。

同様に方程式 39 を次のように修正します。

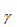注: U と の値は接着回復と接着破壊では異なります。これは活性化エネルギーと活性化体積が、これら 2 つのプロセスにおいて物理的に異なるためです。方程式 40 と 41 は、複合材料疲労の予測に Helius PFA が使用する KTF の基本的な方程式です。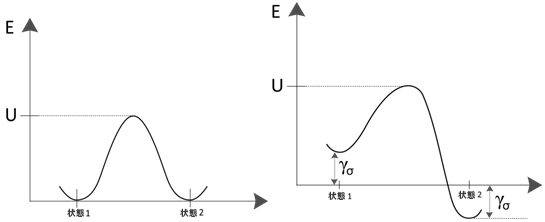

1 活性化体積の正確な定義は、樹脂破断プロセスは原子体積よりもはるかに大きいため、多少あいまいになります。 したがって、通常、活性化プロセスが発生する体積としてのみ定義します。