織物複合材料
KTF を使用して織物複合材料を確認します。
織物単層において疲労荷重時の母材ポケットの微小亀裂は、単層の耐荷重性応答にほとんど影響がありません[22-24]。したがって、織物単層の疲労プロセスにおいて、母材ポケットの微小亀裂は重要な役割を果たさないため、微小亀裂による破損は無視します。
織り交差部のはく離(meta-delaminations)は、疲労荷重時のけん引の相互摩擦効果によって材料ヒステリシスに顕著な影響があることが提示されています[25-26]。また、これらのはく離は、けん引を分離し、疲労荷重時の応力の再分配を可能にすることも提示されています。現在のところ、簡素化するため、疲労解析では織り交差部のはく離は無視します。また、織物ミクロ構造の最終的な破損は、繊維に対して垂直な母材の亀裂により開始すると仮定します。2 つの束内で母材破損が開始すると、その後すぐに、けん引の最終的な破損が発生します。
ここで、疲労破損プロセスの最適化に使用する上記の仮定は、次の一連のイベントとして提案できます。
- 疲労荷重による束内の母材構成の横方向亀裂
- 繊維破損を発生させる疲労荷重による母材構成の縦方向亀裂
最後に、実験データで、疲労荷重による束内の横方向亀裂の開始が報告されることは稀です。適用応力レベルで破損に至るまでのサイクル数に関する情報のみが報告されます。したがって、縦方向亀裂のみが平織物材料の最終的な疲労破損に影響すると仮定します。これは過度な簡略化のように見えますが、織物複合材料は束内の横方向亀裂に対応するように設計されています。けん引の構造は、単層の任意の面内方向における「繊維」応答を提供します。
軸上
平織物単層の面内の任意の荷重により、繊維破断による致命的な破損イベントが最終的に発生します。縦方向亀裂による疲労荷重の最終的な破損は、繊維を結合する母材構成内の亀裂が原因で発生すると上記に説明しました。縦方向亀裂の発生後すぐに、繊維構成内に存在する大量の応力集中のために繊維破損が発生します。
理論的には、一方向材料用に作成された軸上の有効な応力は、織物ミクロ構造にも適用可能です。しかし、前のページに示した体積平均化応力を使用すると、自己平衡化応力は除外されます。このことは、平織物複合材料では、その他の応力成分が自己平衡化するため、純粋なせん断荷重は母材構成に存在する応力のせん断成分のみになることを意味します。純粋なせん断荷重が織物単層の疲労損傷を発生させることが示されていますが、純粋なせん断荷重が最終的な疲労破損に影響する応力を発生させることはありません[22]。したがって、平織物複合材料用の方程式 44 を次のように修正します。

ここで、

方程式 47 は、次のように有効な応力ではなく、破損インデックスを生成するように修正できます。

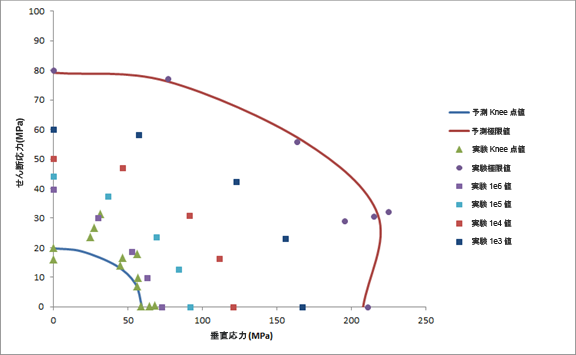
A i の値は、縦方向引張、縦方向圧縮、面内せん断の 3 つの複合材料の静的破損テストから決定されます。方程式 47 に示す破損基準は、実験データと次に示す Predicted Ultimate というラベルの付いた結果に対して検証されました。