ユーザ入力の推奨事項と考慮事項

織物材料入力に関する推奨事項を示します。

前のセクションの説明は、過度に簡略化したアプローチにように見えますが、実験データの制限によりジオメトリの簡略化が強制されます。通常は、繊維体積分率の合計と織物のバランスが良いかアンバランスであるかなどの情報を把握できる程度です。すべての情報の一貫性を維持するために、Composite Material Manager では複合材料の繊維体積分率の合計、単位セルを定義するためのけん引の束体積分率を入力する必要があります。

けん引間隔とそれぞれの束体積分率間のリンクは複雑で、Kuhn と Charalambides [1]により、単位セルに関する議論において開発されました。この論文に記載される議論では、この材料は取り扱われていませんが、ここで、織物ジオメトリに関して適切な説明をするために使用できる、いくつかの推奨事項や基本的な関係を提示する必要があります。

Composite Material Manager によって特性指定される織物複合材料では、けん引繊維体積分率は方程式 3 を使用して、次のように自動的に計算されます。

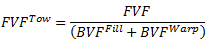、(方程式 4)

一般的な織物複合材料のけん引繊維体積分率は 0.65 ～ 0.85 の範囲にあります。このセクションで提示された推奨事項を使用する場合は、確実に値が許容範囲内に収まるように、計算されたけん引繊維体積分率を確認することをお勧めします。さらに、Composite Material Manager によって出力された、すべての材料特性を確認することを強くお勧めします。出力された構成および複合材料特性が許容可能ではない場合は、許容可能な材料特性が取得されるまで、束体積分率を微調整する必要があります。

バランスが良好な平織物複合材料

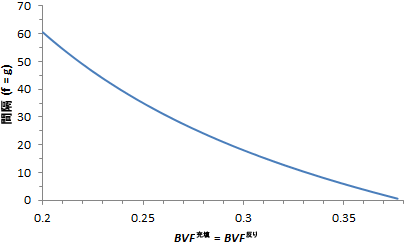
推奨パラメータの説明を開始する前に、まずバランスが良好な平織物複合材料の例を検討します。この例では、束体積分率と間隔が同じであるため、2D の空間を使用して説明することができます。次のプロットは、等しい幅と高さ(34.04 単位)の単位セルに対する束間隔と結果の束体積分率の関係を示しています。束体積分率の計算時に単位は分割されるため、この説明では正確な単位は重要ではありません。メッシュ作成アルゴリズムと単位セルのジオメトリの制限により、バランスが良好な平織物複合材料の許容体積分率値は 0.2 ～ 0.377 の範囲内にある必要があります。バランスが良好な平織物複合材料の束体積分率が分からない場合は、充填および反り束体積分率両方に対して値 0.375 を使用することをお勧めします。

アンバランスな平織物複合材料

アンバランスな平織物複合材料は、ジオメトリが 2 つの異なる束体積分率の関数であるため、本質的に説明がより困難になります。この説明の残りの部分では、最も剛性の高い複合材料応答の方向が、充填方向、つまり 11-方向にあると仮定します。最も剛性の高い応答方向が反りけん引と同じ方向にある場合、次の関係は容易に切り替えることができます。

アンバランスな平織物複合材料では、メッシュ作成アルゴリズムと単位セルのジオメトリは、通常、充填と反りの体積分率の合計が次を満たす必要があります。

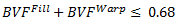、(方程式 5)

および

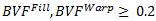、(方程式 6)

これは、充填ギャップ間隔と反りギャップ間隔の関数として、本質的には充填体積分率と反り体積分率で構成された 3D 空間であることに注意してください。この空間を簡略化し、間隔の範囲に関連付けられた体積分率の範囲を理解するために、下のグラフをご覧ください。複数の充填体積分率に対する反り体積分率の許容範囲の関数として、反り間隔に対する充填間隔の比率を表示しています。これらの関係は、一定の反り体積分率、および充填体積分率の範囲に対応するために、簡単に切り替わります。下のグラフを使用して、充填間隔と反り間隔の比率を把握することで、許容可能な充填体積分率および反り体積分率を推定できます。一般的な出発点として、オートデスクでは、複合材料の最も剛性の高い材料応答の方向にある、けん引の束体積分率に対して 0.375 を使用することをお勧めします。

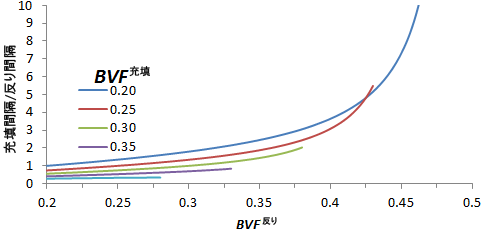
選択したアンバランスな平織物複合材料の充填および反り間隔にアクセスできない場合は、オートデスクでは一般的に許容可能な結果が得られる参照パラメータを用意しています。これらのパラメータの最初のものは、充填けん引に対する、反りけん引の線形密度の比率です。

このパラメータを把握して、充填束体積分率を 0.375 と仮定すると、次の表を使用して、織物複合材料の必要な反り束体積分率を計算できます。

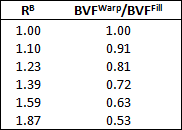
上記の結果から、Composite Material Manager で使用されるマイクロメカニックス モデル開発時になされた仮定を用いて、けん引比率、RB の関数として束体積分率の正確な関係が得られます。上記の説明は、Composite Material Manager を使用して、アンバランスな織物材料を特性設定するための正確な出発点を提供しますが、それでも単位セルのジオメトリを生成するのに必要な情報を取得できない場合もあります。

束間隔やけん引比率にアクセスできない場合のために、オートデスクでは、複合材料の面内剛性を使用して、複合材料の束体積分率を決定するための推奨ガイドラインをいくつか用意しています。複合材料の面内剛性の比率と強化タイプ(ガラスまたは炭素)を把握することで、次の表を使用して、充填および反りの束体積分率を推定できます。ただし、この表にある束体積分率を使用することで、剛性比率がリストされた値と完全に一致するとは限りません。利用できる構成特性に応じて、これらの値は若干変動します。

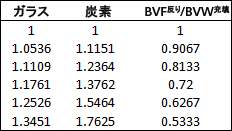
朱子織物

Composite Material Manager 内で使用するために開発された単位セルでは、直交けん引のある平織り、4、5、または 8 枚朱子織り複合材料ミクロ構造のフォームを使用できます。これまでのすべての説明では、良好なバランスまたはアンバランスな平織物複合材料の束体積分率のユーザ入力の推奨事項を中心に行ってきました。朱子織物のミクロ構造では、束体積分率に制限があり、以前に平織物用に提供されていたものとは異なります。

完全単位セル

• 4 枚朱子織物 - 0.24 ≤ BVF ≤ 0.40
• 5 枚朱子織物 - 0.28 ≤ BVF ≤ 0.42
• 8 枚朱子織物 - 0.25 ≤ BVF ≤ 0.41

縮小単位セル

• 4 枚朱子織物 - 0.24 ≤ BVF ≤ 0.4
• 5 枚朱子織物 - 0.28 ≤ BVF ≤ 0.4
• 8 枚朱子織物 - 0.25 ≤ BVF ≤ 0.4

朱子織物の束体積分率の正確な値が分からない場合は、充填および反りの両方の束体積分率で値 0.375 を使用することをお勧めします。

綾織り

マイクロメカニックス モデルは、平織物複合材料料と一部の朱子織りバリエーションに制限されていますが、平織物複合材料料を使用して、綾織りの材料データ セットを生成することができます。ただし、他のバリエーションの朱子織りや綾織りでは、モデルの構造応答の上限は、クロスプライ積層を使用して計算する必要があります。

参考文献

1. Kuhn, J. L. and P.G. Charalambides, 1999, "Modeling of Plain Weave Fabric Composite Geometry," Journal of Composite Materials, Vo. 33, pp. 188-220.