溶接ジョイントの疲労曲線

溶接ジョイントの疲労強度を決定するために、さまざまなタイプの疲れ曲線を使用できます。垂直およびせん断応力の各曲線に対する数式は次のとおりです。

1. 仮想平均応力方法

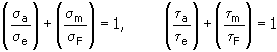
ここで

	σ a 、τ a	垂直(せん断)応力の振幅[MPa, psi]
	σ e 、τ e	一定の強さでの耐久限度 [MPa, psi]
	σ m 、τ m	平均繰返し応力[MPa, psi]
	σ F 、τ F	仮想平均応力 [MPa、psi]
	Ψ	ヘーグダイアグラム目減らし係数[-]
		ジョイント材料ごとに異なる引張と曲げに対する推奨値 Ψ<0.15...0.3>
		- せん断の場合 Ψ <0.1...0.25>

2. 修正グッドマン方法

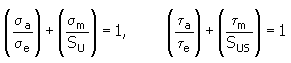
ここで

	σ a 、τ a	垂直(せん断)応力の振幅[MPa, psi]
	σ e 、τ e	一定の強さでの耐久限度 [MPa, psi]
	σ m 、τ m	平均繰返し応力[MPa, psi]
	S U	最大引張強さ [MPa, psi]
	S US	極限せん断強度[MPa, psi]
		S US ≈ 0.8 S U の場合

3. 二次方程式(楕円)方法

変数の説明については、項目 2 の修正グッドマン方法を参照してください。

4. ゲルバー放物線方法

変数の説明については、項目 2 の修正グッドマン方法を参照してください。

5. Keccecioglu, Chester, and Dodge 方法

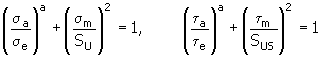
ここで

	σ a 、τ a	垂直(せん断)応力の振幅[MPa, psi]
	σ e 、τ e	一定の強さでの耐久限度 [MPa, psi]
	σ m 、τ m	平均繰返し応力[MPa, psi]
	S U	最大引張強さ [MPa, psi]
	S US	極限せん断強度[MPa, psi]
		S US ≈ 0.8 S U の場合
	a	ジョイントの材料によって決まる指数[-]
		推奨値 a <2.6...20.75>

6. バグシー方法

ここで

	σ a 、τ a	垂直(せん断)応力の振幅[MPa, psi]
	σ e 、τ e	一定の強さでの耐久限度 [MPa, psi]
	σ m 、τ m	平均繰返し応力[MPa, psi]
	S Y	降伏引張強度 [MPa, psi]
	S YS	せん断降伏強さ[MPa, psi]
		S YS ≈ 0.577 S Y の場合

7. ソダーバーグ方法

変数の説明については、項目 6 のバグシー方法を参照してください。