Iterative Solver Parameters dialog

Use this dialog to set up the iterative solver parameters.

Access

Click Tools Job Preferences.
Select Structure Analysis in the left panel of the Job Preferences dialog.
Select Iterative, and then click Parameters.

Dialog elements

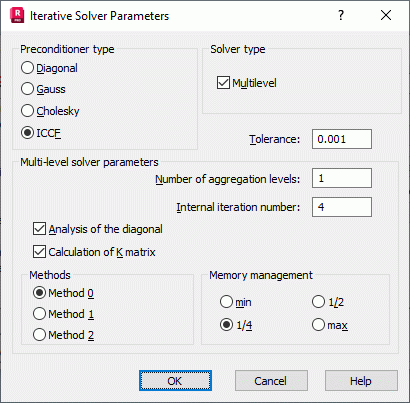
Solver type

Select a solver type:

Multilevel disabled: PCGEBE
Multilevel enabled: AEBEIS (recommended)

Preconditioner types

The PCGEBE and AEBEIS methods are based on the EBE technique with the following preconditioner method types:

Diagonal: Jacobi's method
Cholesky : EBE Cholesky symmetric preconditioning
Gauss: EBE symmetric Cholesky-Gauss-Seidel preconditioning
ICCF: Incomplete Cholesky factorization technique (recommended)

Tolerance

Define the successive iterations (tolerance) carried out till the following condition is met:

|| rk || / || b || ≤ tol

rk= b - K xk

The maximum Euclidean and uniform norm is taken as the vector norm. For instance:

rk= Residual vector

b= right-hand side (load vector)

Xk= solution approximation in the k-th iteration step. This parameter determines the precision of iterations. If you assume that tol=0.001, it means that at least the first three digits of the reaction value will be identical, as in the exact solution obtained by means of the exact solver (frontal or skyline method). It is recommended to assume tol=0.001 for a trial solution and tol = {1.0e-04 - 1.0e-08} for a final solution.

Calculation of K Matrix

If the Calculation of K matrix option is turned on, the respective finite element matrices Ke (e € 1, Nele; where Nele is the number of finite elements in the designed structure) are calculated when the product of the matrix multiplied by vector Kv is calculated.

If the Calculation of K matrix option is turned off, the respective finite element matrices Ke (e € 1, Nele) are taken from the disk.

Note: Enable the Calculation of K matrix if your computer has a high-speed processor and relatively slow disk access. In other cases, it is recommended to turn the option off.

The Calculation of the K matrix option is ignored in ICCF, but works for the following preconditioners:

Diagonal
EBE Gauss
EBE Cholesky

Note: The above mentioned parameters must be determined for both the PCGEBE solver and the AEBEIS solver. The remaining parameters described below should be defined only when the AEBEIS solver has been selected.

Multi-level Solver Parameters

Define the number of aggregation levels. The default value of one assures the minimum number of iterations. These complex calculations will require more disk space and time to process.

It is recommended to assume the following:

Number of Equations	Number of Aggregation
< 20 000	1
20 000 - 50 000	2
50 - 200 000	3-4
> 200 000	4-5

Small sized problems at the coarsest level (SPCL) ensure quick iterations. However, a smaller SPCL increases iterations.

Define the number of internal iterations performed during the smoothing process. Its value typically equals 3 or 4. During analysis of large tasks you may increase the number of internal iterations up to 8.

Enabling the Analysis of the Diagonal improves aggregation by means of the stiffness matrix K. It is recommended to enable this option to accelerate convergence.

Methods

Diagonal, EBE Gauss and EBE Cholesky preconditoners can use any of these methods while ICCF will default to Method 0.

Method 0: A two-level solver with the quickest iterations. The speed of reaching convergence is the slowest, with respect to the number of iterations.

Method 1: A multi-level solver with limited possibilities of smoothing. This approach assures less intense use of memory to solve big problems. This is an excellent alternative to Method 2 when hardware ability is a concern.

Method 2: A multi-level solver with smoothing at every aggregation level. This approach has the best convergence and allows the maximum number of aggregation levels. The requirements imposed on disk space are the smallest in this case. It is recommended to use this method in the case when the number of aggregation levels is larger than 2.

Note: If the number of aggregation levels equals 1, all the methods function alike.

Memory Management

Adjust the memory buffer used to store the matrices of elements and preconditioning elements in the Memory management section. This option works for the following types of preconditioning: Diagonal, EBE Gauss and EBE Cholesky. In the ICCF approach memory management is ignored.

min: assures minimal buffer size, but it may reduce the speed of calculations (default setting).

1/4: A fourth of system memory allocated to calculations.

1/2: A half of system memory allocated to calculations.

max: As much system memory as needed allocated to calculations.

Note: Using a half or all physical memory may lead to problems with the operation of other programs.