Designations applied:
E - Young's modulus
v - Poisson's ratio
G - shear modulus
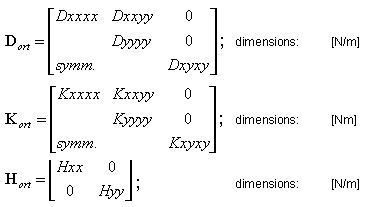
Single-sided unidirectional ribs
h - plate thickness
ha - rib height
a - rib spacing
a1 - rib width
|
Membrane stiffness values: adopted as: s1 = a*h, s2 = (ha-h)*a1 D_XXXX = E*(s1+s2)/a D_YYYY = E*h D_XXYY = v*E*h D_XYXY = G*h D_XXXY = 0 D_YYXY = 0 |
Bending stiffness values: adopted as: hz = h + a1/12, xv = 1 - v*v Dyyyy= E/(12*xv)*a/((a-a1)/(h*h*h)+a1/(hz*hz*hz)) I = moment of inertia of a T-section with flange width a/xv, flange thickness h, total height ha and web thickness a1 K_XXXX = E*I/a K_YYYY = Dyyyy K_XXYY = v*Dyyyy K_XYXY = (1-v)/2*Dyyyy K_XXXY = 0 K_YYXY = 0 |
|
Shear stiffness values: H_XX = 5/6*G*((a-a1)*h + a1*ha)/a H_YY = 5/6*G*h H_XY = 0 |
Double-sided unidirectional ribs
h - plate thickness
ha - rib height
a - rib spacing
a1 - rib width
|
Membrane stiffness: adopted as: s1 = a*h, s2 = (ha-h)*a1 D_XXXX = E*(s1+s2)/a D_YYYY = E*h D_XXYY = v*E*h D_XYXY = G*h D_XXXY = 0 D_YYXY = 0 |
Bending stiffness: adopted as: hz = h + a1/6, xv = 1 - v*v Dyyyy= E/(12*xv)*a/((a-a1)/(h*h*h)+a1/(hz*hz*hz)) I = moment of inertia of a cross-shaped section with flange width a/xv, flange thickness h, total height ha and web thickness a1 K_XXXX = E*I/a; K_YYYY = Dyyyy; K_XXYY = v*Dyyyy; K_XYXY = (1-v)/2*Dyyyy K_XXXY = 0; K_YYXY = 0; |
|
Shear stiffness values: H_XX = 5/6*G*((a-a1)*h + a1*ha)/a H_YY = 5/6*G*h H_XY = 0 |
Single-sided bi-directional ribs
h - plate thickness
ha - rib height
hb - rib height
a - rib spacing
a1 - rib width
b - rib spacing
b1 - rib width.
|
Membrane stiffness values: adopted as: s1x = a*h, s2x = (h-ha)*a1 s1y = b*h, s2y = (h-hb)*b1 D_XXXX = E*(s1x+s2x)/a D_YYYY = E*(s1y+s2y)/b D_XXYY = v*E D_XYXY = G*h D_XXXY = 0 D_YYXY = 0 |
Bending stiffness values: if ha>=hb, then a2 = a1, a1 = a-a1, h2 = ha, b2 = b1, b1 = b-b2, h1 = hb if otherwise (hb>ha), then a2 = b1, a1 = b-b1, h2 = hb, b2 = a1, b1 = a-b2, h1 = ha I11 = InertiaTsec(b/xv, b2, hp, h1) I12 = InertiaTsec(b/xv, b2+a2/6, hp+b2/12, hp+a/12) I21 = InertiaTsec(a/xv, a2, hp, h2) I22 = InertiaTsec(a/xv, (a2+a2+b2/6)/2, hp+b2/12, h2) xv = 1 - v*v GC1 = G*TorsI(b2,h1) GC2 = G*TorsI(a2,h2) D11 = E*a/b/(a1/I11+a2/I12) D22 = E*b/a/(b1/I21+b2/I22) K_XXXX = (ha>=hb) D22:D11 K_YYYY = (ha>=hb) D11:D22 K_XXYY = v*E/12.0*(h3/xv+ h1*h1*h1 *a2*b2/(a*b)) K_XYXY = G*h3/12.0 + (GC1/b+GC2/a)/4.0 K_XXXY = 0.0 K_YYXY = 0.0 xv = 1 - v*v |
|
Shear stiffness values: H_XX = 5/6*G*((a-a1)*h + a1*ha)/a; H_YY = 5/6*G*h; H_XY = 0; |
Unidirectional box floor
h - floor thickness
h1 - lower plate thickness
h2 - upper plate thickness
a - rib spacing
a1 - rib width.
|
Membrane stiffness values: adopted as: s1 = a*h1, s2 = a*h2, s0 = (h-h1-h2)*a1 D_XXXX = E*(s1+s2+s0)/a D_YYYY = E*(h1+h2) D_XXYY = v*E*(h1+h2) D_XYXY = G*(h1+h2) D_XXXY = 0 D_YYXY = 0 |
Bending stiffness values: adopted as: hz1 = h1 + a1/12, hz2 = h2 + a1/12, xv = 1 - v*v Dyyyy= E*a/( (a-a1)/InertiaIsec(1/xv,0,h,h1,h2) + a1/InertiaIsec(1/xv,0,h,hz1,hz2)) Iy = InertiaIsec(a/xv,a1,h,h1,h2) K_XXXX = E*Iy/a K_YYYY = Dyyyy K_XXYY = v*Dyyyy K_XYXY = (1-v)/2*Dyyyy K_XXXY = 0 K_YYXY = 0 |
|
Shear stiffness values: ha = h-h1-h2 H_XX = 5/6*G*((a-a1)*(h1+h2) + a1*ha)/a H_YY = 5/6*G*(h1+h2) H_XY = 0 |
Bi-directional box floor
h - floor thickness
h1 - lower plate thickness
h2 - upper plate thickness
a - rib spacing
a1 - rib width
b - rib spacing
b1 - rib width
|
Membrane stiffness values: adopted as: s1 = a*h1, s2 = a*h2, s0x = (h-h1-h2)*a1, s0y = (h-h1-h2)*b1 D_XXXX = E*(s1+s2+s0x)/a D_YYYY = E*(s1+s2+s0y)/b D_XXYY = v*E*(h1+h2) D_XYXY = G*(h1+h2) D_XXXY = 0.0 D_YYXY = 0.0 |
Bending stiffness values: adopted as: a2 = a1, a1 = a-a2, double b2 = b1, b1 = b-b2, xv = 1 - v*v GC1 = G*TorsI(a2,h-h1-h2) GC2 = G*TorsI(b2,h-h1-h2) Dpl = InertiaIsec(1/xv,0,h,h1,h2) I11 = InertiaIsec(b/xv, b2, h, h1, h2) I12 = InertiaIsec(b/xv, b2+a2/6.0, h, h1+a2/12.0, h2+a2/12.0) I21 = InertiaIsec(a/xv, a2, h, h1, h2) I22 = InertiaIsec(a/xv, a2+b2/6.0, h, h1+b2/12.0, h2+b2/12.0) D11 = E*a/b/(a1/I11+a2/I12) D22 = E*b/a/(b1/I21+b2/I22) K_XXXX = D22 K_YYYY = D11 K_XXYY = v*E*(Dpl+h3/12.0*a2*b2/(a*b)) K_XYXY = (1.0-v)/2.0*E*Dpl+(GC1/b+GC2/a)/4.0 K_XXXY = 0.0 K_YYXY = 0.0 |
|
Shear stiffness values: H_XX = 5.0/6.0*G*((a-a1)*(h1+h2) + a1*h)/a H_YY = 5.0/6.0*G*((b-b1)*(h1+h2) + b1*h)/b H_XY = 0.0 |
Grillage
h - rib height
a - rib spacing
a1 - rib width
b - rib spacing
b1 - rib width
|
Membrane stiffness values: D_XXXX = E*h*a1/a D_YYYY = E*h*b1/b D_XXYY = 0.0 D_XYXY = G*h*(1.-(a-a1)*(b-b1)/(a*b)) D_XXXY = 0.0 D_YYXY = 0.0 |
Bending stiffness values: a2 = a1; a1 = a-a2; b2 = b1; b1 = b-b2 D=E*h3/12, a23=a2*a2*a2, b23=b2*b2*b2 K_XXXX = D * a2/a K_YYYY = D * b2/b K_XXYY = v*D * (a2*b2)/(a*b) K_XYXY = D*(1-v*v*a2*b2/(a*b))/(a*b*(a/a23+b/b23)) K_XXXY = 0.0 K_YYXY = 0.0 |
|
Shear stiffness values: H_XX = 5.0/6.0*G*h*a1/a H_YY = 5.0/6.0*G*h*b1/b H_XY = 0.0 |
Slab on trapezoidal plate
h - plate thickness
h1 - steel plate height
a - steel plate rib spacing
a1 - bottom rib width
a2 - top rib width
Stiffness values D, K and H are calculated in the identical manner as for the single-sided unidirectional ribs type after substituting the following quantities:
a1 = (a1+a2)/2
ha = h+h1.
Material orthotropy
h - plate thickness
n1 stiffness coefficient
n2 stiffness coefficient
The following assumptions are adopted:
E1= E*n1 E2= E*n2
G1= E1*/(2*(1+v)) G2= E2*/(2*(1+v))
G12=sqrt(E1*E2)/(2*(1+v))
H3= h*h*h*/(12*(1-v*v))
|
Membrane stiffness values: D_XXXX = E1 * h/(1-v*v) D_YYYY = E2 * h/(1-v*v) D_XXYY = v * h * sqrt (E1 * E2)/(1- v*v) D_XYXY = G12 * h D_XXXY = 0.0 D_YYXY = 0.0 |
Bending stiffness values: K_XXXX = E1 * H3 = K11 K_YYYY = E2 * H3 = K22 K_XXYY = v * sqrt ( K11 * K22) K_XYXY = (1-v)/2*sqrt(K11*K22) = h*h*h/12*G12 K_XXXY = 0.0 K_YYXY = 0.0 |
|
Shear stiffness values: H_XX = 5/6 * G1 * h H_YY = 5/6 * G2 * h H_XY = 0.0 |
Trapezoidal plate
h - plate height
t - plate thickness
a, a1, a2 - dimensions of a single plate segment (spacing, width values)
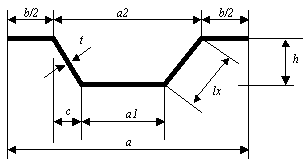
The following assumptions are adopted:
v2= v*v
B = E*t*t*t /(12*(1-v2))
M = E*t/(1-v2)
b = a-a2
c = (a2-a1)/2
lx = sqrt(h*h+c*c)
ca = c/lx
Ax = a1+b+2*lx
e = h*(lx+a1)/Ax
Ix = e*e*b + 2*lx/3 (h*h+3*e*(e-h))+ (e-h)*(e-h)*a1
As = b+2*ca*ca*lx+a1
|
Membrane stiffness values: D_XXXX = M*Ax/a D_YYYY = a/(Ix/B + As/M) D_XXYY = D_YYYY*v D_XYXY = G*t*a/Ax D_XXXY = 0.0 D_YYXY = 0.0 |
Bending stiffness values: K_XXXX = (M*Ix+B*As)/a K_YYYY = B*a/Ax K_XYXY = G*t/a*(Ix + t*t/12*(As*(1+Ax/a)-a)) K_XXXY = 0.0 K_YYXY = 0.0 |
|
Shear stiffness values: H_XX = G*t*5/6*Ax/kx/a H_XY = 0.0 kx = Ax/(2*lx) |
Corrugated plate
h - plate height
t - plate thickness
a - dimension of a single plate segment (spacing)

The following assumptions are adopted:
The equation describing plate geometry:
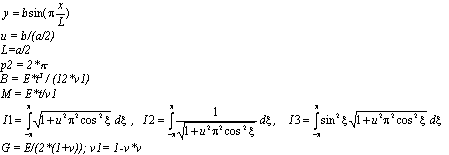
|
Membrane stiffness values: D_XXXX = M*I1/2p D_YYYY = 2p M/(I2+ 12*(h/t)*(b/t)*I3) D_XXYY = D_YYYY*v D_XYXY = 2p G*t /I1 D_YYXY = 0.0 |
Bending stiffness values: K_XXXX = M* b*b*I3/2? K_YYYY = 2p B /I1 K_XYXY = G*t*b*b*I3/2p+G*t*t*t/12*(I2/2p *(1+I1/2p)-1) K_XXXY = 0.0 K_YYXY = 0.0 |
|
Shear stiffness values: H_XX = G*t*5/6*I1/2p H_XY = 0.0 |
Slab composed with a trapezoidal plate
h - slab thickness
h1 - trapezoid plate height
t - trapezoid plate thickness
a, a1, a2 - dimensions of a single plate segment (spacing, widths)
Es - Young's modulus (trapezoid steel)
vs - Poisson's ratio (trapezoid steel)
Eb - Young's modulus (concrete; a value adopted based on a selected material)
vb - Posson's ratio (concrete; a value adopted based on a selected material)

Assumptions:
b = a - a2
e = 0.5*(a-(b+a1))
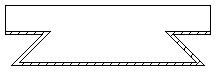
s = sqrt(e*e+h1*h1)
Ab1 = a*h
Ab2 = (a1+e)*h1
As = t*(b+2*e+a1)
Ebx = Eb/(1.0-vb*vb)
Esx = Es/(1.0-vs*vs)
Gb = Eb/(2.0*(1.0+vb))
Gs = Es/(2.0*(1.0+vs))
hx - equivalent height of concrete which equals:
if h+(a-b)/6.0 < h+h1, to h+(a-b)/12.0
if h+(a-b)/6.0 > h+h1, to h+h1/2
hx3 = hx*hx*hx
y0 = (Ebx*(Ab1*(h1+h/2)+a1*h1*h1/2+2*e*h1*h1/3.0)+Es*t*(b*h1+e*h1))/(Ebx*(Ab1+Ab2)+Es*As)
h3 = h*h*h
d3 = h1*h1* h1
e1 = h1+h/2 -y0
e1 = e1*e1
e2 = y0- h1/2
e2 = e2*e2
e3 = (y0-2*h1/3.0)^2
y1 = Ebx*h*h/(2*(Ebx*h+Esx*t));
hd = h+0.5*h1
hd3 = hd*hd*hd
|
Membrane stiffness: D_XXXX = (Ebx*(Ab1+Ab2)+As*Esx)/a D_YYYY = a/(b/(h*Ebx+t*Esx)+(a-b)/(hx*Ebx)) D_XXYY = D_YYYY*vb D_XYXY = Gb*a/((a1+e)/(h+h1)+(b+e)/h) + Gs*t*a/(As/t) D_XXXY = 0.0 D_YYXY = 0.0 |
Bending stiffness: K_XXXX = ( Ebx*(a*h3/12+Ab1*e1+ a1*d3/12 + a1*h1*e2 +e*d3/36 +e*h1/2*e3) + Esx*t*(b*(y0-h1)*(y0-h1) + a1*y0*y0 + e*h1*h1/12 + e*e2))/a K_YYYY = a/(b/(Ebx*(h3/12.0 + h*(y1-h/2)*(y1-h/2)) + Esx*t*y1*y1) + (a-b)/(Ebx*hx3/12.0)) K_XXYY = vb*Ebx*a/(b/h3 + (a-b)/hx3)/12.0 K_XYXY = Gb*h3/12 K_XYXY = = Gb*a/(b/h3 + (a-b)/hd3)/12.0 K_XXXY = 0.0 K_YYXY = 0.0 |
|
Shear stiffness: H_XX = Gb*(Ab1+Ab2)/a*5.0/6.0 H_YY = Gb*a/(b/h + (a-b)/hd)*5.0/6.0 H_XY = 0.0 |
Hollow slab
ha = h - h1 - h2 stiffener height
|
Membrane stiffness: s1 = a*h1, s2 = a*h2, s0 = (h-h1-h2)*a-(3,14*a1*a1/4+c*a1) D_XXXX = E/xv*(s1+s2+s0)/a D_YYYY = E/xv *(h1+h2) D_XXYY = v*E/xv *(h1+h2) D_XYXY = G*(h1+h2) D_XXXY = 0 D_YYXY = 0 |
Bending stiffness: hz1 = h1 + a1/12, hz2 = h2 + a1/12, xv = 1 - v*v, r = a1/2 Dyyyy= E*a/((a-a1)/(InertiaIsec(1/xv,0,h,h1,h2) + a1/InertiaIsec(1/xv,0,h,hz1,hz2)) Iy = InertiaIsec(a/xv,a1,h,h1,h2) + 4*(0,00755*r*r*r*r + 0,2146*r*r*(c/2+0,7766*r)*(c/2+0,7766*r)) If the stiffness of bending in Y direction was disregarded, then Dyyyy = 1,0*e-4*Dyyyy If not, then Dyyyy = Dyyyy K_XXXX = E*Iy/a K_YYYY = Dyyyy K_XXYY = v*Dyyyy K_XYXY = (1-v)/2*Dyyyy K_XXXY = 0 K_YYXY = 0 |
|
Shear stiffness: H_YY = 5/6*G*(h1+h2) H_XY = 0 |