Calculation of quality of triangles (mesh elements)
When triangular mesh is generated, you should define the mesh so that its generated elements are equilateral triangles. Other triangles, especially obtuse triangles, are "worse" mesh elements from a point of view of Finite Elements Method (FEM).
Assuming that a quality coefficient of triangular mesh elements is in range of <0,1>, we accept α coefficient equals 1 for an equilateral triangle.
Calculate the α coefficient for a triangle with ABC apexes from the following formula:
This algorithm is based on calculation of a vector product of two vectors in space.
Calculation of quality of quadrilaterals (mesh elements)
The ideal quadrilateral for creating quadrilateral mesh is a rectangle. A method of calculations of triangle coefficients is used to calculate α coefficient.
Any quadrilateral ABCD is divided into 4 overlapped triangles (ABC, ACD, ABD, and BCD). Calculation of α coefficients is done for particular triangles: { α1, a2, α3, α4} = { α (ABC), α (ACD), α (ABD), α (BCD)}. When these coefficients are calculated, a quadrangle quality coefficient is calculated.
temp1 = α1 * α3;
temp2 = α2 * α4;
if( temp1 * temp2 != 0 )
α= ( temp1 > temp2 ) ? temp2 / temp1 : temp1 / temp2;
α_rect = 0.86602540000000;
α_avg = (α_rect - fabs((α1 + α2 + α3 + α4) / 4. - α_rect))/ α_rect;
if (α_avg < α) α= α_avg;
Calculation of a global mesh quality coefficient
There are 2 ways to calculate a global coefficient:
- The quality values of all mesh elements (triangles, quadrilaterals) are averaged.

where n - mesh element number
- Weighted quality values of all mesh elements (triangles, quadrilaterals) are averaged, where a weight is a mesh element area.
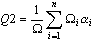
where n - mesh element number, Ω - area