About the block subspace iteration method

The method of block subspace iteration is used to solve the generalized eigenproblem.

Generalized eigenproblems are faced during the modal or buckling analysis of a structure.

Generalized eigenproblem (1)

Where:

K represents the Stiffness matrix.
B = M - mass matrix in the case of dynamic analysis; in the remaining cases B = Ks, where Ks is the stress-stiffness matrix, originating in the linearization of the appropriate non-linear operator in the case of buckling analysis.
λ represents the Eigenvalue.
Φ represents the Eigenvector.

The method of block subspace iteration is preferred when obtaining a considerable number of eigenpairs (eigenvalues and eigenvectors) for a structure. Usually this is more than ten.

Note: The method of block subspace iteration can be applied to divisible structures.

The method of block subspace iteration works with all types of mass matrices i.e. consistent, lumped with rotations, or lumped without rotations. The range of application is limited to the modal analysis. Selecting Lanczos enables the remaining two modes: pseudo-modal and seismic.

The Sturm check option determines the skipped eigenvalues during the verification process.

The method of block subspace iteration consists in simultaneous iterations of a vector in subspace with a determined dimension. Each vector for which the process of convergence has been performed is removed from the working subspace and a new start vector is added in its place. The orthogonality of the vectors is assured in each iterative step. The following convergence criterion is applied:

( 2 )

where:

i, k - number of a mode and number of iteration step, respectively

tol -tolerance, defined in the "Tolerance" edit field.

The results of modal and buckling analyses are determined with certain precision, determined by the following formula:

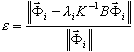( 3 )

If the process of convergence is slow, it is recommended to apply the procedure of shifts in modal analysis:

( 4 )

where:

K_σ = K - σ M,

σ - shift value.

The number of iterations between two successive shifts is treated as the parameter of this procedure.

Note: Avoid setting an excessively small number of iterations between successive shifts. It leads to frequent reinforcement-aggregation and decomposition of the shifted stiffness matrix K_σ. These are particularly time-consuming operations, especially in the case of big structures.

The shifting procedure should not be applied to the analysis of buckling problems because there is a danger of shifting the spectra of eigenvalues in the direction of negative critical load (possibly disregarding positive critical loads) when there are negative eigenvalues for the structure.

Determined eigenpairs are sorted in the following manner | λ1 | ≤ | λ 2 | ≤ ... ≤ | λ n |, which results in locating the minimum parameters of critical load in the upper part of the table with results.