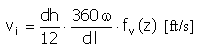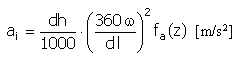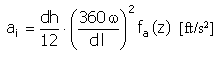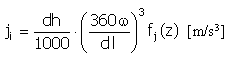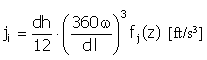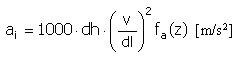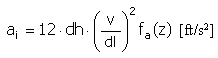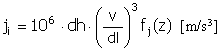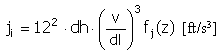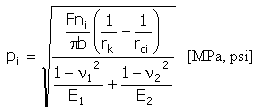Dados de entrada:
- Raio básico r 0 (cames cilíndricas e de disco)
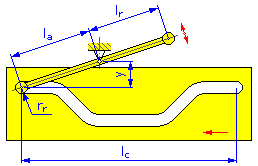
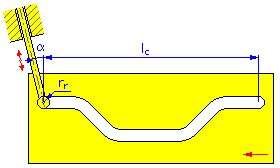
- Comprimento do movimento l c (cames lineares)
- Largura da came b c
- Raio do rolo r r
- Largura do rolo b r (para o cilindro de forma do seguidor)
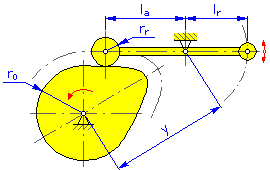
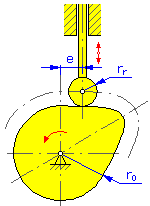
- Excentricidade e (cames de disco para transladar o seguidor)
- Ângulo de excentricidade α (cames de disco lineares e cilíndricas para transladar o seguidor)
- Distância de giro e (cames de disco e lineares para o braço oscilante)
- Comprimento do braço l a (cames de disco e lineares para o braço oscilante)
- Braço de reação l r (cames de disco e lineares para o braço oscilante)
- Velocidade ω (cames de disco e cilíndricas)
- Velocidade v (cames lineares)
- Força sobre o rolo F
- Peso acelerado m
- Capacidade da mola c
- Pressão suportada p A1
- Módulo de elasticidade do material da came E 1
- Coeficiente de Poisson do material da came μ 1
- Pressão suportada p A2
- Módulo de elasticidade do material do seguidor E 2
- Coeficiente de Poisson do material do seguidor μ 2
|
Came de disco |
|
|
|
|
|
Came linear |
|
|
|
|
|
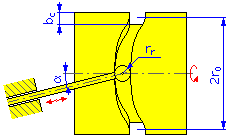
Came cilíndrica |
|
 |
|
|
Diâmetro externo = 2r 0 + b c |
|
|
Diâmetro interno = 2r 0 - b c |
|
Segmentos da came
- Função do movimento f e (z) [ul]
- Coeficiente de marcha atrás k r (só para o movimento parabólico e parabólico com peça linear)
- Coeficiente de peça linear k l (só para o movimento parabólico com peça linear)
- Posição inicial do movimento l 0 [°; mm, polegada]
- Posição final do movimento l [°; mm, polegada]
- Comprimento do movimento do segmento dl = l - l 0 [°; mm, polegada]
- Elevação ao início h 0 [mm, polegada]
- Elevar ao final h máx [mm, polegada]
- Elevar segmento d h = h máx - h 0 [mm, polegada]
Dependências da elevação
Came de disco e cilíndrica
Ângulo de rotação da came ϕ i [°]
Posição relativa real no segmento: z i = (ϕ i - l 0 ) / dl (faixa 0 - 1)
|
Elevação |
e i = dh f e (z) [mm, polegada] |
|
Velocidade |
|
|
|
|
|
Aceleração |
|
|
|
|
|
Impulso |
|
|
|
Came linear
Posição de movimento da came l i [mm, polegada]
Posição relativa real no segmento: z i = (l i - l 0 ) / dl (faixa 0 - 1)
|
Elevação |
e i = dh f e (z) [mm, polegada] |
|
Velocidade |
|
|
Aceleração |
|
|
|
|
|
Impulso |
|
|
|
Funções de movimento
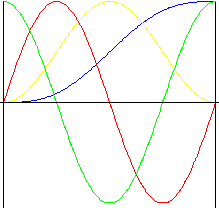
Cicloidal (sinusoidal ampliado)
Este movimento tem excelentes características de aceleração. É usado frequentemente nas cames de alta velocidade por gerar níveis baixos de ruído, vibração e desgaste.
|
|
Elevação |
|
|
Velocidade |
|
|
Aceleração |
|
|
Impulso |
|
Elevação |
f e (z) = z - 0.5/π sem(2πz) |
|
Velocidade |
f v (z) = 1 - cos (2πz) |
|
Aceleração |
f a (z) = 2π sem(2πz) |
|
Impulso |
f j (z) = 4π 2 cos(2πz) |
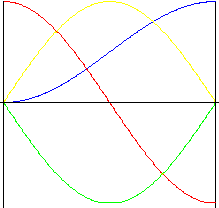
Harmônico (sinusoidal)
Suavidade em velocidade e aceleração durante o curso são as vantagem inerentes a essa curva. No entanto, as alterações instantâneas da aceleração ao princípio e ao final do movimento costumam provocar vibração, ruído e desgaste.
|
|
Elevação |
|
|
Velocidade |
|
|
Aceleração |
|
|
Impulso |
|
Elevação |
f e (z) = 0.5 (1 - cos πz)) |
|
Velocidade |
f v (z) = 0.5 π sem (πz) |
|
Aceleração |
f a (z) = 0.5 π 2 cos(πz) |
|
Impulso |
f j (z) = -0.5π 3 sem(πz) |
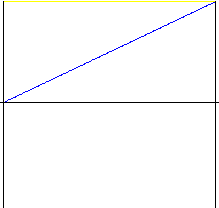
Linear
Movimento simples com um enorme impacto ao princípio e ao final do movimento. Quase nunca é utilizado, apenas em dispositivos muito rudimentares. É aconselhável utilizar um movimento com um princípio e um final alterados (parabólico com uma peça linear).
|
|
Elevação |
|
|
Velocidade |
|
Elevação |
f e (z) = z |
|
Velocidade |
f v (z) = 1 |
|
Aceleração |
f a (z) = 0 |
|
Nota: Para z = 0 e z = 1, o valor correto deveria ser um valor infinito, mas o cálculo não funciona com valores infinitos, pois utiliza um valor zero.
|
|
|
Impulso |
f j (z) = 0 |
|
Nota: Para z = 0 e z = 1, o valor correto deveria ser um valor infinito, mas o cálculo não funciona com valores infinitos, pois utiliza um valor zero.
|
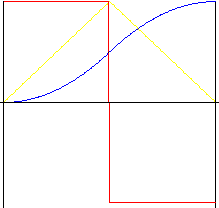
Parabólico (polinômio de 2 ° grau)
Movimento com a menor aceleração possível. No entanto, por causa das alterações de aceleração repentinas ao princípio, meio e final do movimento, são produzidos impactos. O coeficiente inverso permite que no “trecho” central do movimento seja produzida uma alteração na proporção entre aceleração e desaceleração.
simétrico (coeficiente inverso k r = 0,5)
|
|
Elevação |
|
|
Velocidade |
|
|
Aceleração |
|
para z = 0 a 0,5: |
|||
|
Elevação |
fy(z) = 2z 2 |
||
|
Velocidade |
fv(z) = 4z |
||
|
Aceleração |
fa (z) = 4 |
||
|
Impulso |
fa(z) = 0 |
||
|
para z = 0,5 - 1: |
|||
|
Elevação |
fy(z) = 1 - 2(1 - z) 2 |
||
|
Velocidade |
fv(z) = 4 (1 - z) |
||
|
Aceleração |
fa (z) = -4 |
||
|
Impulso |
fj(z) = 0 |
||
|
Nota: Para z = 0 e z = 1, o valor correto deveria ser um valor infinito, mas o cálculo não funciona com valores infinitos, pois utiliza um valor zero.
|
|||
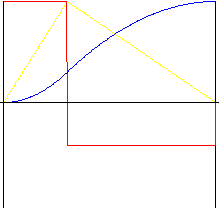
não simétrico
k r - coeficiente inverso (na faixa 0,01 a 0,99)
|
|
Elevação |
|
|
Velocidade |
|
|
Aceleração |
|
para z = 0 a k r : |
|||
|
Elevação |
f e (z) = z 2 / k r |
||
|
Velocidade |
f v (z) = 2z / k r |
||
|
Aceleração |
f a (z) = 2 / k r |
||
|
Impulso |
f j (z) = 0 |
||
|
para z = k r a 1: |
|||
|
Elevação |
f e (z) = 1 – (1 – z) 2 / (1 – k r ) |
||
|
Velocidade |
f v (z) = 2 (1 – z) / (1 – k r ) |
||
|
Aceleração |
f a (z) = -2 / (1 - k r ) |
||
|
Impulso |
f j (z) = 0 |
||
|
Nota: Para z = 0 e z = 1, o valor correto deveria ser um valor infinito, mas o cálculo não funciona com valores infinitos, pois utiliza um valor zero.
|
|||
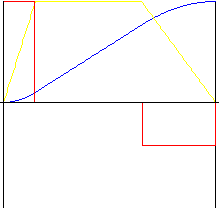
Parabólico com peça linear
Fornece uma aceleração e uma desaceleração mais aceitáveis que as do movimento linear. O coeficiente inverso permite que no “trecho” central do movimento seja produzida uma alteração na proporção entre aceleração e desaceleração. O coeficiente da peça linear permite definir o tamanho relativo da peça linear do movimento.
|
|
Velocidade |
|
|
Aceleração |
|
|
Impulso |
k r - coeficiente inverso (na faixa 0,01 a 0,99)
k l - coeficiente da peça linear (na faixa 0 a 0,99)
k z = 1 + k l / (1 - k l )
k h = (1 - k l ) / (1 + k l )
|
para z = 0 a k r / k z : |
|||
|
Elevação |
f e (z) = k h z 2 k z 2 / k r |
||
|
Velocidade |
f v (z) = 2 k h z k z 2 / k r |
||
|
Aceleração |
f a (z) = 2 k h k z 2 / k r |
||
|
Impulso |
f j (z) = 0 |
||
|
para z = k r / k z a r / k z + k l : |
|||
|
Elevação |
f e (z) = (z - 0.5 k r / k z ) 2 / (1 + k l ) |
||
|
Velocidade |
f v (z) = 2 / (1 + k l ) |
||
|
Aceleração |
f a ( z) = 0 |
||
|
Impulso |
f j (z) = 0 |
||
|
para z = k r / k z + k l a 1: |
|||
|
Elevação |
f e (z) = 1 - k h (1 - z) 2 k z 2 / (1 - k r ) |
||
|
Velocidade |
f v (z) = 2 k h (1 - z) k z 2 / (1 - k r ) |
||
|
Aceleração |
f a (z) = -2 k h k z 2 / (1 - k r ) |
||
|
Impulso |
f j (z) = 0 |
||
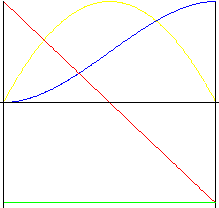
Polinômio de 3 ° grau (parábola cúbica)
Movimento com impactos menores que o movimento parabólico.
|
|
Elevação |
|
|
Velocidade |
|
|
Aceleração |
|
|
Impulso |
|
Elevação |
f e (z) = (3 -2z) z 2 |
|
Velocidade |
f v (z) = (6 - 6z) z |
|
Aceleração |
f a (z) = 6 - 12z |
|
Impulso |
f j (z) = -12 |
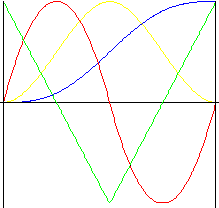
Polinômio de 4 ° grau
Movimento com impactos menores que o movimento do polinômio de terceiro grau.
|
|
Elevação |
|
|
Velocidade |
|
|
Aceleração |
|
|
Impulso |
|
para z = 0 - 0,5 |
||
|
Elevação |
f e (z) = (1 - z) 8z 3 |
|
|
Velocidade |
f v (z) = (24 - 32z) z 2 |
|
|
Aceleração |
f a (z) = (48 - 96z) z |
|
|
Impulso |
f j (z) = 48 - 192z |
|
|
para z = 0,5 - 1 |
||
|
Elevação |
f e (z) = 1 - 8z (1 - z) 3 |
|
|
Velocidade |
f v (z) = (32z - 8) (1 - z) 2 |
|
|
Aceleração |
f a (z) = (48 - 96z) (1 - z) |
|
|
Impulso |
f j (z) = 194z - 144 |
|
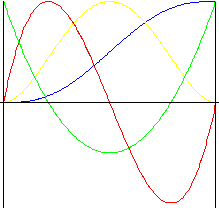
Polinômio de 5 ° grau
Movimento com impactos menores que o movimento do polinômio de terceiro grau.
|
|
Elevação |
|
|
Velocidade |
|
|
Aceleração |
|
|
Impulso |
|
Elevação |
f e (z) = (6z 2 - 15z + 10) z 3 |
|
Velocidade |
f v (z) = (z 2 - 2z + 1) 30z 2 |
|
Aceleração |
f a (z) = (2z 2 - 3z + 1) 60z |
|
Impulso |
f j (z) = (6z 2 - 6z + 1) 60 |
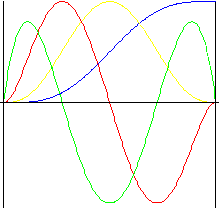
Polinômio de 7 ° grau
Suavidade em todas as fórmulas, incluído o impulso.
|
|
Elevação |
|
|
Velocidade |
|
|
Aceleração |
|
|
Impulso |
|
Elevação |
f e (z) = (-20z 3 + 70z 2 - 84z + 35) z 4 |
|
Velocidade |
f v (z) = (-z 3 + 3z 2 - 3z + 1) 140z 3 |
|
Aceleração |
f a (z) = (-2z 3 + 5z 2 - 4z + 1) 420z 2 |
|
Impulso |
f j (z) = (-5z 3 + 10z 2 - 6z + 1) 840z |
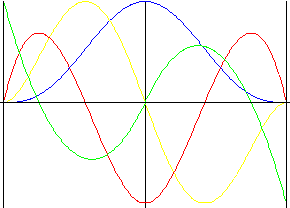
Polinômio não simétrico de 5 ° grau
Similar ao polinômio de 5º grau, mas com uma reversão forçada da elevação.
|
|
Elevação |
|
|
Velocidade |
|
|
Aceleração |
|
|
Impulso |
|
Peça 1 |
||
|
Elevação |
f e (z) = 1 - (8 (1 - z) 3 - 15 (1 - z) 2 + 10) (1 - z) 2 / 3 |
|
|
Velocidade |
f v (z) = (2 (1 - z) 3 - 3 (1 - z) 2 + 1) (1 - z) 20 / 3 |
|
|
Aceleração |
f a (z) = -(8 (1 - z) 3 - 9 (1 - z) 2 + 1) 20 / 3 |
|
|
Impulso |
f j (z) = (4 (1 - z) 2 - 3 (1 - z)) 40 |
|
|
Parte 2 |
||
|
Elevação |
f e (z) = (8z 3 - 15z 2 + 10) z 2 / 3 |
|
|
Velocidade |
f v (z) = (2z 3 - 3z 2 + 1) z 20/3 |
|
|
Aceleração |
f a (z) = (8z 3 - 9z 2 + 1) 20/3 |
|
|
Impulso |
f j (z) = (4z 2 - 3z) 40 |
|
Duplo harmônico
Suavidade em todas as fórmulas, incluindo o impulso com reversão forçada da elevação.

|
Peça 1 |
||
|
Elevação |
f e (z) = cos(0.5π (1 - z)) 4 |
|
|
Velocidade |
f v (z) = π (0.5 sem(πz) - 0.25 sem(2πz)) |
|
|
Aceleração |
f a (z) = 0.5 π 2 (cos(πz) - cos(2πz)) |
|
|
Impulso |
f j (z) = π 3 (-0.5 sem(πz) + sem(2πz)) |
|
|
Parte 2 |
||
|
Elevação |
f e (z) = 1 - cos(0.5π z) 4 |
|
|
Velocidade |
f v (z) = π (0.5 sem(πz) + 0.25 sem(2πz)) |
|
|
Aceleração |
f a (z) = 0.5 π 2 (cos(πz) + cos(2πz)) |
|
|
Impulso |
f j (z) = -π 3 (0.5 sem(πz) + sem(2πz)) |
|
Comparação dos valores relativos máximos
|
Movimento |
Velocidade |
Aceleração |
Impulso |
|
Cicloidal (sinusoidal ampliado) |
2 |
6,28 |
39,5 |
|
Harmônico (sinusoidal) |
1,57 |
4,93 |
15,5 |
|
Linear |
1 |
∞ |
∞ |
|
Parabólico (polinômio de 2 º grau) |
2 |
4 |
∞ |
|
Polinômio de terceiro grau |
1,5 |
6 |
12 |
|
Polinômio de 4 º grau |
2 |
6 |
48 |
|
Polinômio de 5 º grau |
1,88 |
5,77 |
60 |
|
Polinômio de 7 º grau |
2,19 |
7,51 |
52,5 |
|
Polinômio não simétrico de 5 º grau |
1,73 |
6,67 |
40 |
|
Duplo harmônico |
2,04 |
9,87 |
42,4 |
Outras dependências
Força sobre o rolo
|
F i = F + m a i + c e i [N, lb] |
Força normal
|
Fn i = F i / cos (γ i ) [N, lb] |
Carga momentânea
|
T i = F i r i tão (γ i ) [Nmm, lb polegada] |
Pressão específica (hertz)
|
|
|
|
b = mín (b v, b k ) |