A equação do fluxo de calor dentro do contorno mostrado abaixo pode ser apresentada como segue.
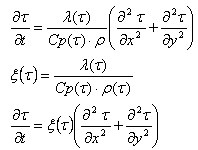
em que:
C p – Calor específico (J/kg*K)
λ – Condutividade térmica (W/m*K)
ρ – Peso da unidade (kg/m 3).
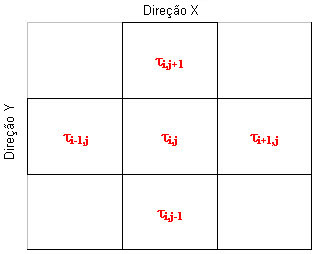
Na notação diferencial, as equações de fluxo de calor podem ser gravadas como:
.
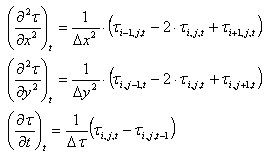Essas equações produzem:
.
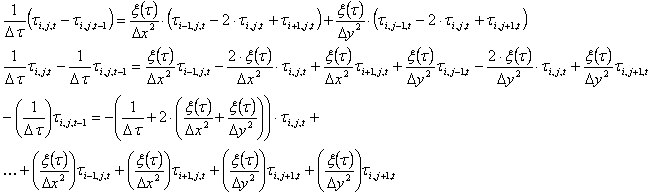Portanto, para os nós K, o sistema de equações M[KxK] x τ[K] = B[K] será resolvido.
Aproximações adotadas
Quando é necessário conhecer a temperatura atual para determinar os coeficientes não descritos por equações, a aproximação dos intervalos de tempo anteriores é aplicada (diferença adiante).
Para a etapa de tempo constante, o seguinte é obtido:
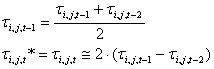
que permite determinar:
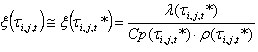
para a etapa i = 1 t i,j,1 * = t i,j,o.
Condições dos limites
Na formulação geral do problema, são adicionadas condições de limite de terceiro tipo, que são responsáveis por:
- Convecção
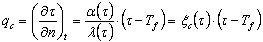
em que:
n – Normal à aresta
Tf –Temperatura no ambiente externo do contorno identificado com a temperatura do fogo.
Assumindo que o coeficiente de convecção a seja independente da temperatura e que as aproximações sejam adotadas discutidas anteriormente, o seguinte é obtido:
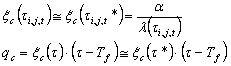. - Radiação
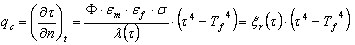
em que:
n – Normal à aresta
T f – Temperatura no ambiente externo do contorno identificado com a temperatura do fogo
Φ – Coeficiente de configuração
ε m – Fator de emissão do elemento
ε f – Fator de emissão de fogo
σ – Constante de Boltzman 5,65*10 8 (W/m 2 *K 4 ).
Adotando as aproximações discutidas anteriormente, é obtido o seguinte:
.
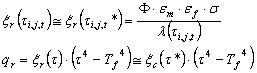Suposições adotadas para a norma DTU P 92-701
- Desenvolvimento de incêndios no tempo
O fogo descrito em um formato discreto (tabular) com base na seguinte fórmula:
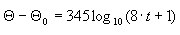(seção 4 DTU P 92-701, figura 11) O fogo descrito em um formato discreto (tabular) com base na seguinte fórmula:
em que t expresso em [min]
que permite descrever a temperatura do fogo como:
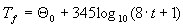
Os valores discretos são selecionados de tal forma que nenhum incremento de temperatura maior do que 30% é realizado em qualquer incremento de tempo. A interpolação linear é executada entre esses valores.
Uma descrição do desenvolvimento de incêndio no tempo é incluída no arquivo Fire_DTU.t
- Condutividade térmica do concreto
A dependência de condutividade térmica é apresentada em um formato tabular (seção 3.15 DTU P 92-701).
Uma descrição do comportamento da condutividade térmica dependendo da temperatura é fornecida no arquivo Lambda_DTU.la.
- Peso unitário do concreto
É independente da temperatura e é igual a 2400 [kg/m3].
Uma descrição do comportamento do peso da unidade dependendo da temperatura é fornecida no arquivo Ro_DTU.cp.
- Calor específico de concreto
Ele é independente da temperatura e é igual a 921,096 [J/kg *K], ou seja, 0,22 [kcal/kg * OC] (seção 3.16 DTU P 92-701).
Uma descrição do comportamento específico do calor, dependendo da temperatura, é fornecida no arquivo Cp_DTU.cp.
- Coeficiente de redução da capacidade de concreto
O coeficiente de redução da capacidade de concreto é apresentado em um formato tabular (seção 3.13 DTU P 92-701).
Uma descrição do comportamento da redução da capacidade de concreto dependendo da temperatura é fornecida no arquivo fic_DTU.cfc.
- Coeficiente de redução da capacidade de aço
O coeficiente de redução da capacidade do aço é apresentado em um formato tabular (seção 3.13 DTU P 92-701).
Uma descrição do comportamento da redução da capacidade do aço dependendo da temperatura é fornecida no arquivo fiy_DTU_1_2.cfy.
No caso de aço tipos 3 e 4 serem usados, defina o arquivo fiy_DTU_3_4.cfy, em vez de um padrão.
- Parâmetros de cálculo
Coeficientes de radiação:
Φ*ε m*ε f = 0,85 de forma análoga ao coeficiente (seção 4 DTU P 92-701)
Os coeficientes acima devem ser entendidos como:
Φ – Coeficiente de configuração
εm – Fator de emissão de elementos
εf – Fator de emissão de fogo
Coeficiente de convecção:
α = 6,9 [W/m2*K] = 6,0 [kcal/m2*h*oC] (seção 4 DTU P 92-701)
Suposições adotadas para a norma EN 1992-1-2
- O desenvolvimento do fogo no tempo de acordo com a EN 1991-1-2
O fogo descrito em um formato tabular discreto com base na seguinte fórmula:
em que:
t expresso em [min]
assumindo a temperatura inicial 20[ 0 C],
que permite descrever a temperatura do fogo como:
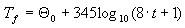. Os valores discretos são selecionados para que nenhum incremento de temperatura maior do que 30% ocorra em qualquer incremento de tempo. A interpolação linear é executada entre esses valores.
Uma descrição do desenvolvimento do incêndio no tempo é incluída no arquivo Fire_EC2_N.t.
No caso de outros tipos de incêndio serem usados, em vez de um arquivo padrão, defina o seguinte:
fogo externo (seção 3.2.2 EN 1991-1-2): Fire_EC2_E.t
incêndio de hidrocarbonetos (seção 3.2.3 EN 1991-1-2): Fire_EC2_H.t
- Condutividade térmica do concreto
A dependência da condutividade térmica é apresentada em um formato tabular (seção 3.4 EN 1992-1-2) – com base no valor mais baixo da condutividade térmica. A interpolação linear é executada entre esses valores.
Uma descrição do comportamento de condutividade térmica dependendo da temperatura é incluída no arquivo Lambda_EC2_L.la.
No caso de o valor superior ser usado, em vez de um arquivo padrão, o usuário deve definir o seguinte:
Lambda_EC2_U.la
- Peso unitário do concreto
A dependência do peso unitário é apresentada em um formato tabular (seção 3.3.2(3) EN 1992-1-2). A interpolação linear é executada entre esses valores.
Uma descrição do comportamento do peso unitário dependendo da temperatura é incluída no arquivo Ro_EC2.cp.
- Calor específico de concreto
A dependência de calor específico é apresentada em um formato tabular (seção 3.3.2(1) e 3.3.2(2) EN 1992-1-2) com base em valores para a umidade de 1,5%. A interpolação linear é executada entre esses valores.
Uma descrição do comportamento específico do calor dependendo da temperatura é incluída no arquivo Cp_EC2_m015.cp.
No caso de outros valores de umidade de concreto serem usados, em vez de um arquivo padrão, defina o seguinte:
0% de umidade: Cp_EC2_m000.cp
3% de umidade: Cp_EC2_m030.cp
- Coeficiente de redução da capacidade de concreto
A dependência do coeficiente de redução para a capacidade de concreto é apresentada em um formato tabular (seção 4.2.4.2 EN 1992-1-2) com base em valores para concreto com agregado de silicato. A interpolação linear é executada entre esses valores.
Uma descrição do comportamento da redução da capacidade de concreto dependendo da temperatura é incluída no arquivo fic_EC2_Si.cfc.
No caso de o concreto com agregado de calcário ser usado, em vez de um arquivo padrão, defina o seguinte: fic_EC2_Ca.cfc.
- Coeficiente de redução da capacidade de aço
A dependência do coeficiente de redução da capacidade do aço é apresentada em um formato tabular (seção 3.2.3 EN 1992-1-2) com base nos valores do aço laminado a quente de classe N. A interpolação linear é executada entre esses valores.
Uma descrição do comportamento da redução da capacidade do aço dependendo da temperatura é incluída no arquivo fiy_EC2_Nhr.cfy.
Caso outros tipos sejam usados, em vez de um arquivo padrão, defina o seguinte:
Aço de classe N laminado a frio: fiy_EC2_Ncw.cfy.
Aço de grau X: fiy_EC2_X.cfy.
- Parâmetros de cálculo
coeficientes de radiação:
Φ = 1,0 – coeficiente de configuração (seção 3.1(6) EN 1991-1-2)
ε m = 0,8 – fator de emissão do elemento (seção 3.1(6) EN 1991-1-2)
ε f = 1,0 – fator de emissão do incêndio (seção 3.1(6) EN 1991-1-2)
coeficiente de convecção:
α ce = 25 [W/m2*K] no lado exposto ao fogo (seção 3.2.1 EN 1991-1-2)
α cu = 9,0 [kcal/m2*h*oC] no lado não exposto ao fogo (seção 3.1(5) EN 1991-1-2)
Cálculo da capacidade para a norma BAEL – colunas axialmente comprimidas
Dados necessários para os cálculos:
f cj – Resistência do concreto automaticamente transferida do módulo de coluna de CA do Robot.
Φ b – Coeficiente do concreto dependendo da temperatura Φ b (τ). Nesse caso, “τ” é uma temperatura média dentro da seção
f e – Resistência do aço automaticamente transferida do módulo de coluna de CA do Robot.
φ si – Coeficiente para aço dependendo da temperatura φ s(τ). Nesse caso, “τ” é uma temperatura na i-ésima barra
l – Altura da coluna
N – Carga máxima aplicada à coluna
α – Coeficiente de transferência automática do módulo de coluna de CA
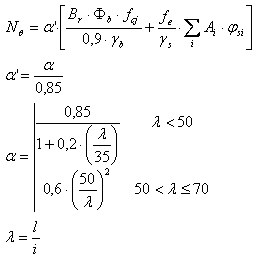
B r = A c - 0,01*u c
Br – Área de seção reduzida
A c – Área de seção
u c – Perímetro da seção
γ b – Coeficiente para concreto 1.3
γ s – Coeficiente para aço 1.0
A i – Área da i-ésima barra de armadura
Capacidade da coluna:
N/NQ > 1,0